“Enquanto as leis matemáticas se referem à realidade, não são absolutas e, enquanto são absolutas, não se referem à realidade."
Albert Einstein
Hoje, vamos explorar um tema fascinante nos conjuntos numéricos: os intervalos reais! Você já se perguntou como representar intervalos abertos, fechados ou infinitos? Não se preocupe, estou aqui para guiar vocês. Prestem atenção, pois esses conceitos são essenciais não apenas para a matemática do ensino médio, mas também para as temidas provas do ENEM e vestibulares!
O que é um intervalo?
Vamos explorar juntos o intrigante conceito de intervalos na matemática. Para aqueles que precisam de um lembrete das aulas passadas, um intervalo refere-se a um conjunto, ou seja, todos os elementos entre dois valores, abrangendo-os completamente.
Ao falar de intervalos, entramos em um terreno de fenômenos periódicos, aqueles que se repetem de maneira específica. Imagine um conjunto de números reais, representado por R ou, se preferir, visualize uma linha graduada de números reais.
Denominamos um intervalo como o conjunto de números reais situados entre dois valores, sejam eles positivos ou negativos, indicados por "a" e "b". Podemos enxergar esse intervalo como os pontos em uma linha, cuja marcação está precisamente entre "a" e "b".
Para ilustrar, considere o intervalo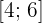 
. Este intervalo representa o conjunto de números reais "
" tal que 
e x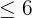 
.
Agora, focando nos sinais matemáticos, os números positivos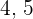 
e 
estão todos inclusos neste intervalo, onde "x" é maior que 4 e menor ou igual a 6. Se você busca auxílio para entender esses conceitos, que tal contar com um professor de matemática a domicílio para orientá-lo?
Adiante, exploraremos diversos tipos de intervalos, tais como o intervalo fechado, o intervalo aberto, a interseção entre dois ou mais intervalos (também conhecido como intervalo semi-fechado ou semi-aberto) e a união de intervalos.
E para dar vida a esses conceitos, vamos observar como um professor de matemática aplica os intervalos, considerando números positivos e negativos, conjuntos definidos, casas decimais e diferentes contextos matemáticos.
Desifrando a escrita dos intervalos matemáticos
Vamos explorar a arte de expressar intervalos na matemática. Ao delinear os limites de um intervalo, utilizamos colchetes e discernimos entre intervalos abertos (
, 
; 
), intervalos fechados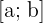 
, e intervalos semiabertos 
.
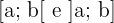A escrita de intervalos envolve conceitos como conjuntos convexos, finitos e contáveis, todos fundamentais no cálculo de intervalos. Ao registrar os limites, é crucial seguir uma ordem matemática: começamos pelo limite inferior e, em seguida, apresentamos o limite superior. Jamais devemos escrever em ordem decrescente, pois isso seria ilógico.
Quando os colchetes estão fechados, significa que cada extremidade pertence ao intervalo. Já quando estão abertos, indica que os limites estão excluídos do intervalo. Vale ressaltar que intervalos não devem ser confundidos com conjuntos de números representados por chaves.
Por exemplo, considere o conjunto de números inteiros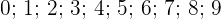 
, incluindo todos os dígitos de 
a 
.
Ao designar conjuntos abstratos, utilizamos a notação com letras, emprestada do cálculo literal. No cálculo de intervalos, frequentemente encontramos notações como:
denota o conjunto de números naturais,
denota o conjunto de inteiros relativos,
denota o conjunto de números decimais,
denota o conjunto de números racionais (aqueles que podem ser escritos como um quociente de dois inteiros relativos),
denota o conjunto de números reais,
denota a interseção de dois conjuntos,
denota a união de dois intervalos.
Embora possa parecer complicado e abstrato inicialmente, com a prática, os intervalos se tornam uma ferramenta fácil de usar. Eles representam a transcrição aritmética de declarações matemáticas, permitindo visualizar dados por meio de diagramas circulares ou linhas retas graduadas.
Apesar de não ser possível calcular intervalos diretamente em calculadoras, a repetição de exercícios é essencial para assimilar corretamente os elementos e caracteres utilizados na escrita dos intervalos. Agora que você compreende como transcrever intervalos, explore como esses símbolos são empregados para expressar conceitos matemáticos, como destacado por Jean Rouaud:
Normalmente, uma vida se inscreve entre dois números que delimitam o curso terrestre, a entrada e a saída, a cargo deste, o evocado matemático, para resolver esta equação cheia de incógnitas que coloca o entre dois.
Aprenda tudo o que precisa com um curso de matemática do zero.
Mas, como se resolve um intervalo e quais são eles?
Como resolver um intervalo?
Vamos agora explorar o processo de resolver um intervalo, como fazemos em uma aula de matemática. Não se preocupe, apenas leia com atenção e siga o raciocínio visualizando um diagrama para compreender o que está contido no conjunto, o que faz parte dele e o que está excluído.
Um cuidado especial é necessário! Analise com atenção o significado dos colchetes, pois eles são cruciais para determinar se um terminal pertence ou não ao intervalo. Então, como resolver um intervalo? Esteja preparado para iniciar o cálculo dos intervalos.
Se você compreende como interpretar os sinais matemáticos, será capaz de distinguir os seguintes tipos de intervalos:
Intervalo fechado
Vamos aprofundar nosso entendimento sobre o intervalo fechado. Este intervalo contém os limites que o definem, ou seja, os pontos que o delimitam. Existem diversas formas de representá-lo, considerando dois números reais, a e b, tal que x seja o conjunto de reais:
,
,
.
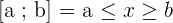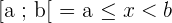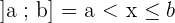
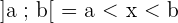Quando os colchetes estão fechados, significa que x é maior ou igual a a e menor ou igual a b. Se os colchetes estiverem abertos, x é estritamente maior que a e estritamente menor que b.
Perceba, há diversas formas de definir este conjunto, oferecendo um conjunto variado de possibilidades e definições. Se sentir necessidade, você pode sempre contar com um curso de matematica online ou presencial, além de muitos conteúdos online com aulas explicativas que irão te ajudar a praticar cada vez mais.
Intervalo aberto
Vamos agora adentrar no intrigante universo do intervalo aberto. Considerando dois números distintos, a e b, temos as seguintes representações:
,
,
,
.
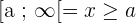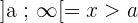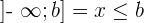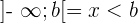Refere-se a um intervalo aberto quando um dos limites é infinito. Nesse contexto, não temos clareza sobre onde o intervalo se inicia ou termina.
E para aprofundar ainda mais seus conhecimentos, explore tudo sobre aritmética!
Intervalo infinito
Vamos explorar o conceito fascinante dos intervalos infinitos! Quando falamos de um intervalo infinito, estamos lidando com conjuntos de números reais que se estendem indefinidamente em uma direção, seja para valores positivos ou negativos. A representação desses intervalos envolve os termos "
" (mais infinito) e "
" (menos infinito).
Ao compreender o intervalo infinito, você poderá descrever conjuntos formados por todos os números reais que são maiores que um valor específico (usando "") ou menores que um valor determinado (usando ""). Vamos mergulhar nesse conceito intrigante e explorar suas aplicações matemáticas.
Intersecção de intervalos
A interseção entre os intervalos 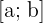e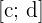 
representa o conjunto de números reais incluídos tanto em 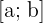quanto em 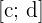. Utilizamos o símbolo arredondado "∩" para denotar a interseção.
Considerando quatro inteiros positivos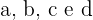 
, a interseção (denominada por ) entre esses dois intervalos pode ser expressa de duas maneiras equivalentes:
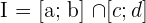ou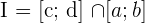 
Por exemplo:
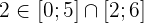porqu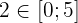e
e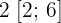 
Para determinar a interseção de dois intervalos, é recomendável representar graficamente os conjuntos em uma linha real. Dessa forma, é possível visualizar como cada elemento está posicionado e entender a propriedade comutativa, ou seja, os elementos compartilhados entre ambos os conjuntos.
Segue um vídeo explicativo para te ajudar no estudo dos intervalos:
União de intervalos
Agora, vamos mergulhar no conceito de união de intervalos, representando o conjunto de números reais x que pertencem tanto ao intervalo [a; b] quanto ao intervalo [c; d].
A operação de união é simbolizada pelo sinal ∪. Você já se perguntou o que é a mediana em matemática?
Consideremos quatro números imaginários, a, b, c e d, de modo que a união U entre esses dois intervalos seja expressa de duas maneiras equivalentes:
U = [a; b] ∪ [c; d] ou U = [c; d] ∪ [a; b]
Por exemplo :
2 ∈ [0; 5] ∪ [2; 6] porque 2 ∈ [0; 5]
3,8 ∈ [0; 5] ∪ [2; 6] porque 3,8 ∈ [0; 6]
Para visualizar a união de dois intervalos, representamos ambos em um eixo graduado, marcando o conjunto de números do primeiro intervalo e o conjunto de números do segundo intervalo.
Que tal criar um cone 3D usando conceitos matemáticos avançados?
Neste exploratório matemático sobre intervalos numéricos, desvendamos conceitos que vão além dos números e adentram o fascinante universo da representação gráfica e lógica. A compreensão dos intervalos fechados, abertos, infinitos, e suas operações de interseção e união, oferece uma base sólida para a interpretação de fenômenos matemáticos em diversas áreas, desde cálculos avançados até análises estatísticas complexas.
Ao compreender a linguagem dos intervalos, você não apenas ganha habilidades matemáticas práticas, mas também desbloqueia portas para a resolução de problemas do mundo real.
Ao compreender a linguagem dos intervalos, você não apenas ganha habilidades matemáticas práticas, mas também desbloqueia portas para a resolução de problemas do mundo real. Seja na física, na economia ou em qualquer campo que envolva grandezas numéricas, os intervalos se revelam como ferramentas essenciais. Assim, ao aprofundar seu conhecimento sobre esses conceitos, você fortalece sua base matemática e se prepara para enfrentar desafios cada vez mais complexos com confiança e destreza. Concluímos, portanto, este mergulho nos intervalos numéricos com a certeza de que esses fundamentos enriquecem não apenas seu entendimento matemático, mas também sua capacidade de pensar logicamente e resolver problemas de maneira eficaz.
Gostou desse artigo? Deixe uma nota!
Loading...
De verdade, isso me ajudou bem mais do que um bimestre de aulas de mat, eu consegui compreender bem, muito obrigada
Que bom, Ana Luiza! Ficamos muito felizes em te ajudar no seu bimestre!
Nao estou conseguindo fazer esse exercicios de matemática,caracterizar por intervalos o segundo trimestre do ano
Gostou muito de aprender com vocês