Temas
Simplifique as seguintes frações algébricas:
a) 
Extraímos o fator comum  na expressão do numerador e do denominador, assim
na expressão do numerador e do denominador, assim
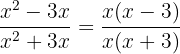
Agora, “cancelamos o fator comum”, assim nossa simplificação fica como
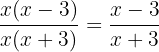
b) 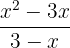
Extraímos o fator comum  no numerador
no numerador
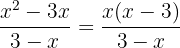
Multiplicamos o numerador e denominador por  , assim, obteremos uma fração equivalente
, assim, obteremos uma fração equivalente
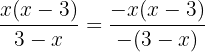
Distribuindo o sinal no denominador, teremos

Cancelando o fator comum no denominador e numerador, obteremos
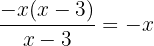
c) 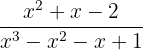
Aplicando o teorema do resto:


Dividimos por Ruffini tanto a expressão do numerador como a do denominador
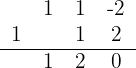
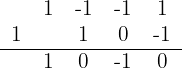
Temos uma divisão exata, assim  e, portanto,
e, portanto,
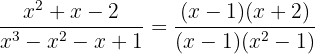
Simplificamos cancelando o fator comum do numerador e do denominador
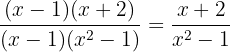
Observe que o denominador  , no entanto, nenhum destes fatores está no numerador, dessa forma, não podemos cancelar ou simplificar mais nesse sentido, por outro lado podemos escrever a expressão como
, no entanto, nenhum destes fatores está no numerador, dessa forma, não podemos cancelar ou simplificar mais nesse sentido, por outro lado podemos escrever a expressão como
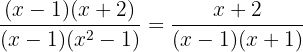
qualquer das duas expressões da igualdade são corretas e válidas.
d) 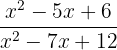
Utilizando a fórmula quadrática obtemos as raízes do polinômio do numerador e do polinômio do denominador, isso vai nos ajudar a poder expressar os polinômios como multiplicação de binômios definidos pelas suas raízes
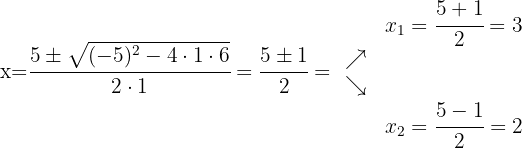
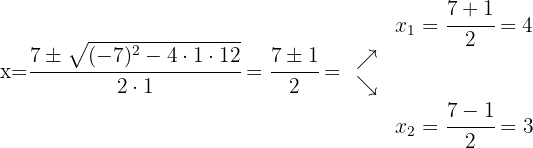
Fatoramos: 
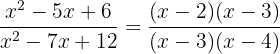
Simplificamos
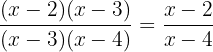
e) 
Utilizando a fórmula quadrática obtemos as raízes do polinômio do numerador e do polinômio do denominador, isso vai nos ajudar a poder expressar os polinômios como multiplicação de binômios definidos pelas suas raízes
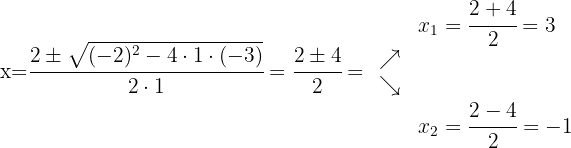
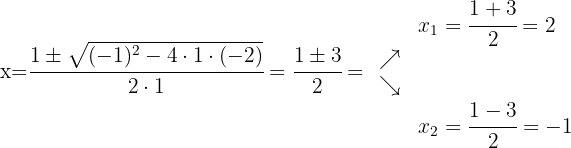
Fatoramos: 

Simplificamos

f) 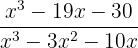
Utilizamos o teorema do resto e a regra de Ruffini no numerador para encontrar as raízes inteiras
Os divisores de  são: {
são: { }
}

Dividimos por Ruffini
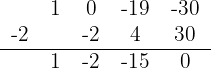
O numerador cumpre

Podemos continuar fatorando o trinômio do mesma maneira ou utilizando a fórmula quadrática
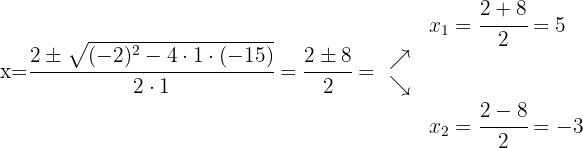

Tiramos o fator comum no denominador 

Para fatorar o trinômio utilizamos a fórmula geral

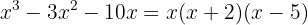
Assim, nossa expressão inicial pode ser escrita como
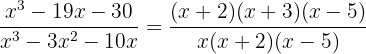
Simplificamos

Faça a seguinte soma de frações algébricas
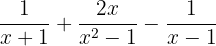
Some as frações algébricas: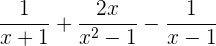
Temos que encontrar o denominador comum, para isso temos que encontrar o m.m.c dos denominadores. Observe que
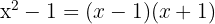
Portanto
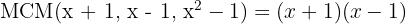
Dividimos o denominador comum entre os denominadores das frações e multiplicamos o resultado pelo numerador correspondente
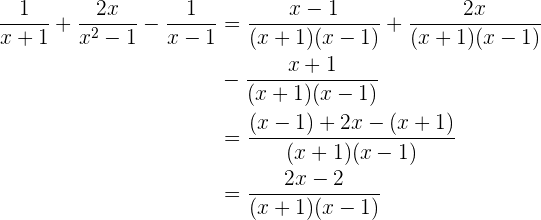
Extraímos o fator comum 

Simplificamos
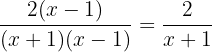
Subtração de frações algébricas

Subtraia as frações algébricas:
Temos que passar para denominador comum, para isso temos que encontrar o m.m.c dos denominadores. Observe que

Portanto

Dividimos o denominador comum entre os denominadores das frações e multiplicamos o resultado pelo numerador correspondente e fazemos a operação
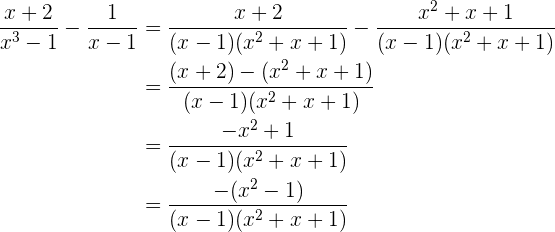
Além disso, sabemos que  , assim, obteremos
, assim, obteremos
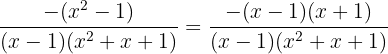
Simplificamos

Divisão de frações algébricas
Divida as frações algébricas:
a) 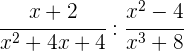
A divisão de duas frações algébricas é outra fração algébrica cujo numerador é o produto do numerador da primeira pelo denominador da segunda; e como denominador, o produto do denominador da primeira pelo numerador da segunda.
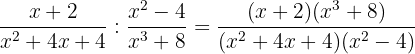
O segundo binômio é uma soma ao cubo: 
O trinômio do denominador é um trinômio do quadrado perfeito e o binômio é uma diferença de quadrados que fatora como uma soma pela diferença.

Simplificamos
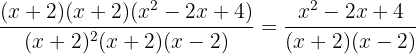
ou então

b) 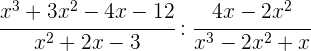
Fazendo a divisão, teremos
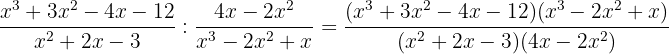
O primeiro fator podemos decompor mediante o teorema do resto e a divisão com Ruffini.
Extraímos o fator comum no segundo fator  , logo sobrará um trinômio do quadrado perfeito do qual vamos expressar como um binômio ao quadrado.
, logo sobrará um trinômio do quadrado perfeito do qual vamos expressar como um binômio ao quadrado.
O primeiro fator do denominador é um trinômio do segundo grau do qual vamos fatorar utilizando a fórmula geral.
No segundo fator tiramos o fator comum  . Assim, nossa expressão original ficaria dessa forma
. Assim, nossa expressão original ficaria dessa forma
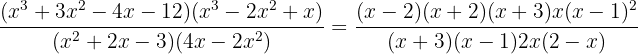
simplificando um pouco
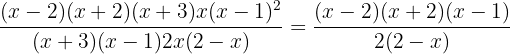
Multiplicamos por  o numerador e denominador, obtendo assim uma fração equivalente.
o numerador e denominador, obtendo assim uma fração equivalente.
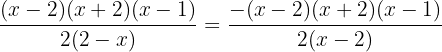
Simplificamos
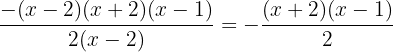
Produto de frações algébricas mistas
Resolva:
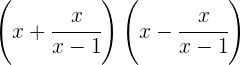
Resolva: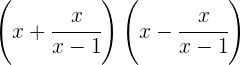
Temos uma soma pela diferença que vamos expressar como uma diferença de quadrados, portanto
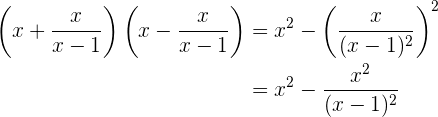
Passamos para denominador comum
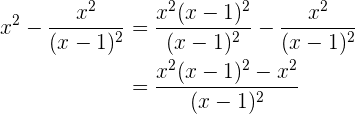
Tiramos o fator comum  e fazemos a operação
e fazemos a operação
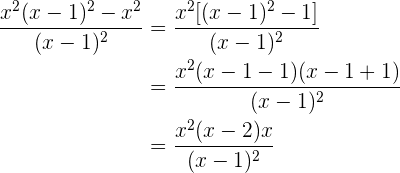
Multiplicamos
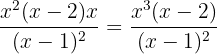
Razão de 2 frações algébricas
Efetue:
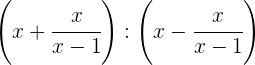
Efetue:
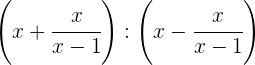
Passamos para denominador comum
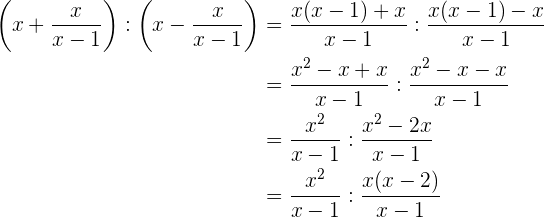
A divisão de duas frações algébricas é outra fração algébrica cujo numerador é o produto do numerador da primeira pelo denominador da segunda; e como denominador, o produto do denominador da primeira pelo numerador da segunda.
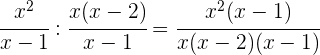
Simplificamos
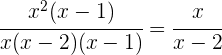
Exercício de frações algébricas
Faça:

Faça: 
Primeiro somamos 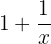 e fazemos o contrário com o resultado, depois voltamos a somar e assim sucessivamente até encontrar nosso resultado.
e fazemos o contrário com o resultado, depois voltamos a somar e assim sucessivamente até encontrar nosso resultado.
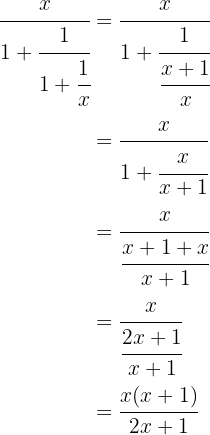
Resumir com IA:














