Temas
A tabela de derivadas, utilizada amplamente no estudo de cálculo, auxilia na compreensão das relações entre variáveis em diversas funções matemáticas. Derivadas são ferramentas que descrevem a taxa de variação de uma variável em relação a outra, sendo um dos conceitos centrais da análise matemática e das ciências aplicadas. Charles Goodhart, na London School of Economics em 1947, apresentou 4 componentes fundamentais para o estudo de derivadas: direção, propriedade, tempo e taxa. No campo da matemática, uma derivada é uma ferramenta que descreve a relação entre duas ou mais variáveis, avaliando como uma mudança em uma variável afeta outra.
Uma das principais utilidades das tabelas de derivadas é fornecer fórmulas padronizadas para facilitar o cálculo de derivadas de funções comuns, como potências, funções trigonométricas, exponenciais e logarítmicas. Essas tabelas ajudam a economizar tempo e a reduzir erros, especialmente ao lidar com funções mais complexas.
As derivadas são fundamentais porque permitem analisar como pequenas mudanças na variável de entrada (independente) afetam a variável de saída (dependente). Isso é especialmente útil em diversos campos, como a física, para estudar velocidades e acelerações, e na economia, para avaliar taxas de crescimento ou de declínio em diferentes cenários.
Por exemplo, no mercado financeiro, as derivadas são utilizadas para modelar e prever mudanças nos valores de ativos com base em variáveis relacionadas, como tempo ou taxa de juros. A análise permite traçar tendências e avaliar o impacto de variações externas, oferecendo informações essenciais para investidores e economistas.
Além disso, as derivadas são aplicadas para traçar linhas de tendência em gráficos, especialmente quando existe uma correlação temporal entre variáveis. Nesse contexto, a derivada ajuda a determinar a inclinação da curva em cada ponto, permitindo identificar padrões de comportamento ao longo do tempo.
A seguir, apresentamos uma tabela com algumas das funções mais frequentes encontradas em livros didáticos de cálculo e suas respectivas derivadas:

Abaixo, confira a classificação das fórmulas de derivação:

Derivadas Básicas (Imediatas)
Derivada de uma constante

Derivada de x

Derivada de uma função afim

Derivada de uma potência

Derivada de uma raiz

Derivada da raiz quadrada
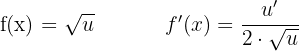
Derivada de uma soma

Derivada de uma constante multiplicada por uma função

Derivada de um produto
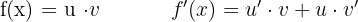
Derivada de uma constante dividida por uma função
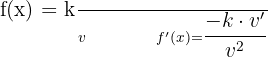
Derivada de um quociente
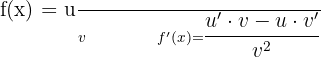
Derivadas Exponenciais e Logarítmicas
Derivada da função exponencial
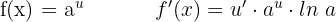
Derivada da função exponencial de base e

Derivada de um logaritmo
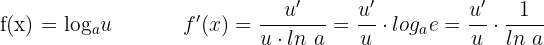
Derivada de um logaritmo natural (neperiano)

Derivadas trigonométricas
Derivada do seno

Derivada do cosseno

Derivada da tangente
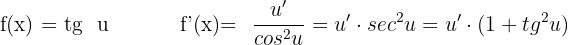
Derivada da cotangente
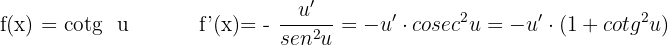
Derivada da secante
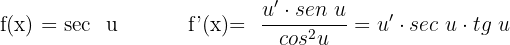
Derivada da cossecante
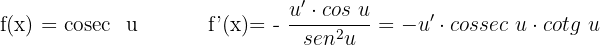
Derivadas trigonométricas inversas
Derivada do arco seno

Derivada do arco cosseno
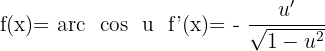
Derivada do arco tangente
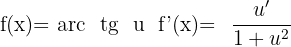
Derivada do arco cotangente
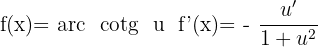
Derivada do arco secante
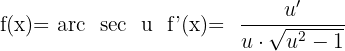
Derivada do arco cossecante
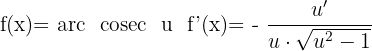
Outras fórmulas importantes
Derivada da função potencial-exponencial
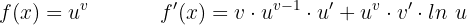
Regra da cadeia
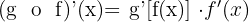
Fórmula de derivada implícita

Resumir com IA:












