Temas
Os exercícios que resolveremos a seguir são exemplos de:
- Fatoração de um binômio
- Fatoração de um trinômio quadrado perfeito
- Fatoração de um trinômio quadrado perfeito
- Fatoração de um trinômio do segundo grau
- Fatoração de um polinômio do quarto grau
- Fatoração de um polinômio de terceiro grau incompleto
- Ordem da equação para facilitar a fatoração

Exercícios de fatoração para obter as raízes dos polinômios
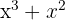
1Para fatorar 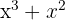 , notamos que
, notamos que  é fator comum de ambos os termos
é fator comum de ambos os termos
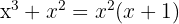
2Sabemos que as raízes é o valor que toma  se a equação é igual a zero, então dado
se a equação é igual a zero, então dado 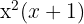 , existem 2 casos: quando
, existem 2 casos: quando  e quando
e quando 
Assim, as raízes são  y
y 
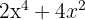
1Para fatorar 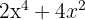 , notamos que
, notamos que 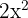 é fator comum de cada um dos termos
é fator comum de cada um dos termos
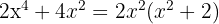
2Neste caso existe apenas a raiz  , já que o polinômio
, já que o polinômio  não têm raízes, isto é, não existe um número real
não têm raízes, isto é, não existe um número real  assim
assim 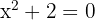

1Aplicamos a diferença de quadrados
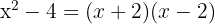
2Igualando cada fator a zero obtemos as raízes
 y
y 
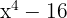
1Aplicamos a diferença de quadrados

2Aplicamos novamente a diferença de quadrados no segundo fator

3Igualando cada fator a zero, obtemos as raízes
 y
y 
Lembre-se que o fator  não possui raízes reais
não possui raízes reais
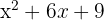
1Estamos diante de um trinômio quadrado perfeito, que pode ser escrito como um binômio ao quadrado, para qual temos que fazer as seguintes perguntas
Qual numero elevado ao quadrado dá  ?, qual número elevado ao quadrado dá
?, qual número elevado ao quadrado dá 
e comprovar que o dobro do produto dos dois resultados é igual a 
2A premissa satisfaz o  e
e  , assim, a fatoração é expressada da seguinte maneira
, assim, a fatoração é expressada da seguinte maneira

3Igualando cada fator a zero, obtemos as raízes
 e dizemos que é uma raiz dupla
e dizemos que é uma raiz dupla

1Neste caso usaremos a fórmula geral para equações do segundo grau da qual devemos igualar a zero, isto é  . Encontramos os valores de
. Encontramos os valores de  (raízes da equação) utilizando a fórmula geral:
(raízes da equação) utilizando a fórmula geral:
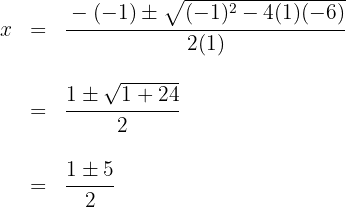
Quando resolvido, obtemos as raízes 
2Neste caso os fatores de cada equação são:
 .
.

1Igualamos o polinômio a zero e fazemos uma mudança de variável 
substituindo nossa nova variável, temos 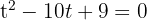
2Resolvendo a equação do segundo grau
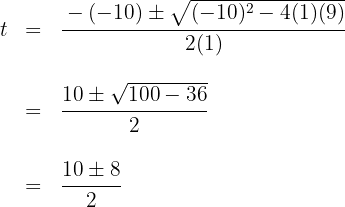
Quando resolvidos, obtemos as raízes 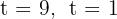
3Agora, na nossa mudança de variável teríamos que  ; desfazemos a mudança de variável e obtemos as raízes
; desfazemos a mudança de variável e obtemos as raízes

4Neste caso os fatores da equação são
 .
.
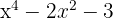
1Igualamos o polinômio a zero e fazemos uma mudança de variável 
Substituindo nossa nova variável, temos 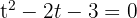
2Resolvemos a equação do segundo grau

Quando resolvidos, obtemos as raízes 
3Agora na nossa mudança de variável teríamos que  ; desfazemos a mudança de variável e obtemos as raízes
; desfazemos a mudança de variável e obtemos as raízes
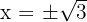 ; mas
; mas 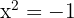 não possui soluções reais
não possui soluções reais
4Neste caso os fatores da equação são
 .
.
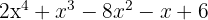
1 Pegamos os divisores do termo independente, que são,  .
.
2 Aplicando o teorema do resto saberemos para quais valores a divisão é exata.

3 Dividimos por Ruffini.
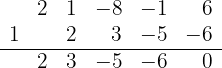
Como a divisão é exata,  é uma raiz e o polinômio é expressado como
é uma raiz e o polinômio é expressado como

4 Continuamos fazendo as mesmas operações no segundo fator. Voltamos a tentar por  porque o primeiro fator poderia estar elevado ao quadrado.
porque o primeiro fator poderia estar elevado ao quadrado.

Assim,  não é raiz do segundo fator. Tentamos com
não é raiz do segundo fator. Tentamos com 
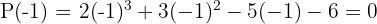
5 Dividimos por Ruffini.
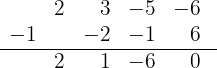
Como a divisão é exata,  é uma raiz e o polinômio é expressado como:
é uma raiz e o polinômio é expressado como:
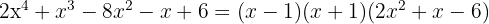
6 O terceiro fator pode ser encontrado aplicando a equação do segundo grau, tal como temos feito, ainda que haja o inconveniente de que apenas possamos encontrar raízes inteiras.
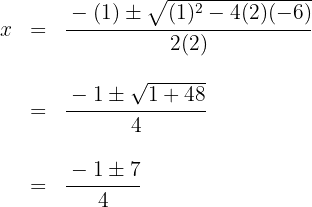
As raízes são 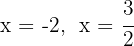 e o polinômio é expressado como:
e o polinômio é expressado como:
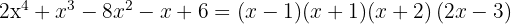

1 Pegamos os divisores do termo independente, que são, 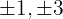 .
.
2 Aplicando o teorema do resto saberemos para quais valores a divisão é exata.
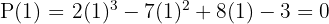
3 Dividimos por Ruffini.
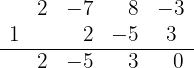
Como a divisão é exata,  é uma raiz e o polinômio é expresso por
é uma raiz e o polinômio é expresso por

4 Continuamos fazendo as mesmas operações no segundo fator. Voltamos a tentar por  porque o primeiro fator poderia estar elevado ao quadrado.
porque o primeiro fator poderia estar elevado ao quadrado.

5 Dividimos por Ruffini.

Como a divisão é exata,  é uma raiz dupla e o polinômio é expresso por
é uma raiz dupla e o polinômio é expresso por
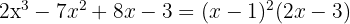
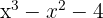
1 Pegamos os divisores do termo independente, que são, 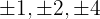 .
.
2 Aplicando o teorema do resto saberemos para quais valores a divisão é exata.
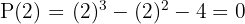
3 Dividimos por Ruffini.
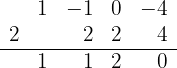
Como a divisão é exata,  é uma raiz e o polinômio é expressado por
é uma raiz e o polinômio é expressado por
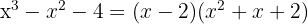
4 O segundo fator pode ser encontrado aplicando a equação do segundo grau, tal como temos feito, ainda que haja o inconveniente de que apenas possamos encontrar raízes inteiras.
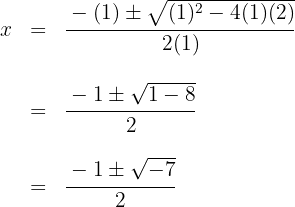
Como o discriminante é negativo, o polinômio não possui raízes inteiras. Assim, a única raiz é  e o polinômio é expresso por
e o polinômio é expresso por
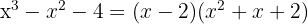
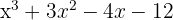
1 Pegamos os divisores do termo independente, que são, 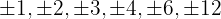 .
.
2 Aplicando o teorema do resto saberemos para quais valores a divisão é exata.

3 Dividimos por Ruffini.
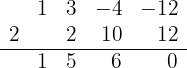
Como a divisão é exata,  é uma raiz e o polinômio é expressado por
é uma raiz e o polinômio é expressado por
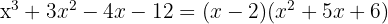
4 O segundo fator pode ser encontrado aplicando a equação do segundo grau, tal como temos feito, ainda que haja o inconveniente de que apenas possamos encontrar raízes inteiras.
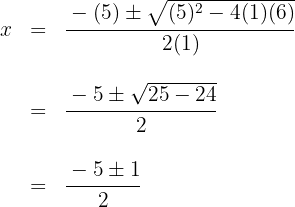
As raízes do segundo fator são 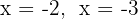 e o polinômio é expressado por
e o polinômio é expressado por
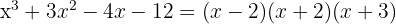
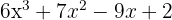
1 Pegamos os divisores do termo independente, que são,  .
.
2 Aplicando o teorema do resto saberemos para quais valores a divisão é exata.
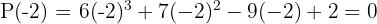
3 Dividimos por Ruffini.

Como a divisão é exata,  é uma raiz e o polinômio é expressado por
é uma raiz e o polinômio é expressado por

4 O segundo fator pode ser encontrado aplicando a equação do segundo grau, tal como temos feito, ainda que haja o inconveniente de que apenas possamos encontrar raízes inteiras.
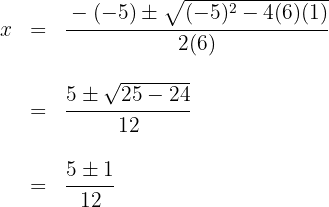
As raízes do segundo fator são  e o polinômio é expressado por
e o polinômio é expressado por

Exercícios de fatoração de polinômios
a) 
Tiramos o fator comum 
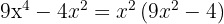
Escrevemos a diferença de quadrados como uma soma pela diferença
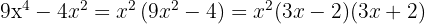
b) 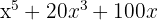
Tiramos o fator comum 

Temos um trinômio quadrado perfeito que podemos expressar como um binômio ao quadrado
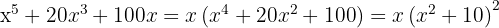
c) 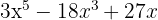
Tiramos o fator comum 
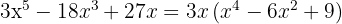
Temos um trinômio quadrado perfeito que podemos expressar como um binômio ao quadrado

Escrevemos a diferença de quadrados como uma soma pela diferença
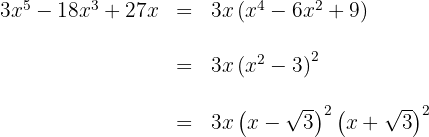
d) 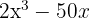
Tiramos o fator comum 
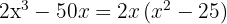
Escrevemos a diferença de quadrados como uma soma pela diferença

e) 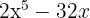
Tiramos o fator comum 

Escrevemos a diferença de quadrados como uma soma pela diferença
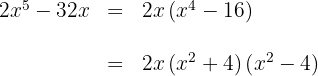
O segundo fator é um polinômio irredutível ou primo
O terceiro fator é uma diferença de quadrado que fatoramos como uma soma pela diferença
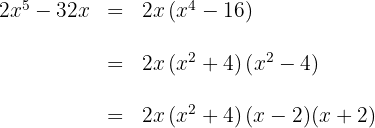
f) 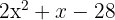
Igualamos o trinômio do segundo grau a zero e resolvemos a equação

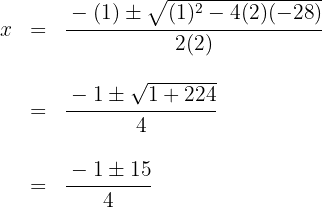
As raízes são 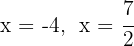 e o polinômio é expressado por
e o polinômio é expressado por
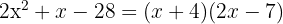
Exercícios de decomposição de polinômios em fatores
a) 
Neste exercício podemos fazer uma dupla extração de fator comum. Nos dois primeiros somandos extraímos  e nos dois últimos extraímos
e nos dois últimos extraímos 

Tiramos o fator comum 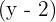

b) 
é uma diferença de quadrados
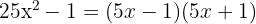
c) 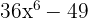
A diferença de quadrados é igual à soma pela diferença
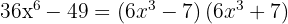
d) 
Um trinômio quadrado perfeito é igual a um binômio ao quadrado
O quadrado de  é
é  , o quadrado de
, o quadrado de  é
é  e o dobro do primeiro
e o dobro do primeiro  pelo segundo
pelo segundo  é
é 

e) 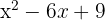
Um trinômio quadrado perfeito é igual a um binômio ao quadrado
O quadrado de  é
é  , o quadrado de
, o quadrado de  é
é  e o dobro do primeiro
e o dobro do primeiro  pelo segundo
pelo segundo  é
é 
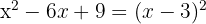
f) 
Um trinômio quadrado perfeito é igual a um binômio ao quadrado
O quadrado de  é
é  , o quadrado de
, o quadrado de  é
é  e o dobro do primeiro
e o dobro do primeiro  pelo segundo
pelo segundo  é
é 
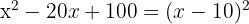
g) 
Um trinômio quadrado perfeito é igual a um binômio ao quadrado
O quadrado de  é
é  , o quadrado de
, o quadrado de  é
é  e o dobro do primeiro
e o dobro do primeiro  pelo segundo
pelo segundo  é
é 

h) 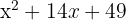
Um trinômio quadrado perfeito é igual a um binômio ao quadrado
O quadrado de  é
é  , o quadrado de
, o quadrado de  é
é  e o dobro do primeiro
e o dobro do primeiro  pelo segundo
pelo segundo  é
é 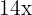
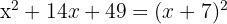
i) 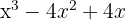
Tiramos fator comum

Temos outro trinômio quadrado perfeito
O quadrado de  é
é  , o quadrado de
, o quadrado de  é
é  e o dobro do primeiro
e o dobro do primeiro  pelo segundo
pelo segundo  é
é 
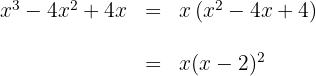
j) 
Tiramos fator comum
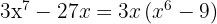
Transformamos a diferença de quadrados em uma soma pela diferença

Aplicamos a soma e diferença de cubos

k) 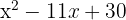
Igualamos o polinômio a zero
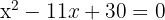
Resolvemos a equação do segundo grau
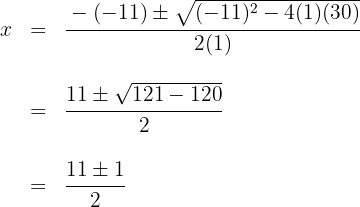
As raízes são 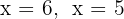 e o polinômio é expressado por
e o polinômio é expressado por

l) 
Resolvemos a equação do segundo grau

As raízes são 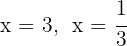 e o polinômio é expressado por
e o polinômio é expressado por
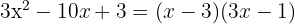
m) 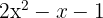
Resolvemos a equação do segundo grau
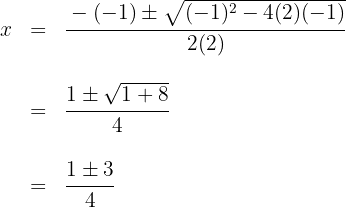
As raízes são 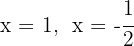 e o polinômio é expressado por
e o polinômio é expressado por

Resumir com IA:













