Temas
Propriedades fundamentais dos expoentes inteiros
1 Qualquer número 
elevado ao expoente 1 é igual ao próprio número :
2 Qualquer número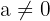 
elevado à potência 0 é igual a 1:
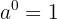
Observação: a expressão 
é uma forma indeterminada, ou seja, não possui valor definido.
3 O resultado de elevar qualquer número a uma potência 
par é sempre positivo. Assim,
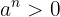
quando 
para algum 
.
Observação: é mais fácil lembrar observando que:
ou seja, qualquer número (positivo ou negativo) elevado a uma potência par tem resultado positivo.
4 O resultado de elevar qualquer número a uma potência ímpar tem o mesmo sinal de . Ou seja,
e
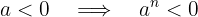
quando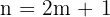 
para algum .
Observação: podemos lembrar dessa expressão com a expressão:
5 Os exponentes negativos seguem a seguinte propriedade (para ):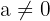
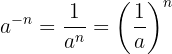
ou seja, é igual ao recíproco da base elevado ao expoente positivo.
Exemplos
Vamos considerar os exemplos abaixo:
1 
, 
, 
2 
, 
3 
pois 6 é um número par. Da mesma forma,
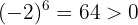
4 
já que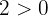 
e 3 é ímpar. De modo semelhante,
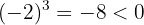
uma vez que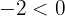 
5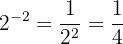 
Expoentes racionais
Definimos as raízes dos números reais da seguinte maneira:
Definição: dado um número 
, a raiz enésima de 
é o número tal que,
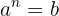
e escrevemos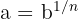 
ou 
.
Por meio dos radicais, introduzimos as potências racionais. Valem as seguintes propriedades:
1 Por definição,
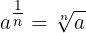
2 Também por definição,
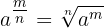
3 E ainda,
Observação: a raiz par de um número negativo não está definida no conjunto dos números reais. Nesses casos, dizemos que a raiz não existe.
Exemplos
1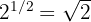 
2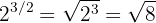 
3 
Leis dos expoentes de mesma base
As seguintes propriedades valem para quaisquer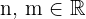 
e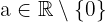 
. Em alguns casos, usar 
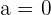pode gerar indeterminações.
1 O produto de potências com a mesma base é igual à base elevada à soma dos expoentes:
2 A divisão de potências com a mesma base é igual à base elevada à diferença dos expoentes:
3 Uma potência elevada a outra potência é igual à base elevada ao produto dos expoentes:
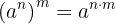
Observação: observe os parênteses da expressão anterior. Primeiro calculamos 
e depois elevamos a 
. Isso é diferente de
que quase nunca é igual, ou seja,
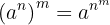
Exemplos
Veja os exemplos a seguir:
1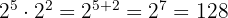 
2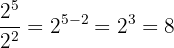 
3 
Operações com potências de mesmo expoente
As seguintes propriedades valem para quaisquer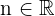 
e 
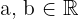com 
.
1 O produto de duas potências com o mesmo expoente é igual ao produto das bases elevado a esse expoente. Ou seja:
2 A divisão de duas potências com o mesmo expoente é igual à divisão das bases elevadas ao expoente:
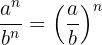
Exemplos
Veja os exemplos a seguir:
1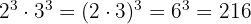 
2 
Exercícios
Calcule as potências a seguir:
a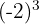
b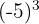
c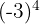
a Observe que a base é negativa e o expoente é ímpar. Portanto, o resultado é negativo:
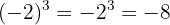
b A base é negativa e o expoente é par. Assim, o resultado é positivo:
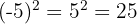
c Novamente, a base é negativa e o expoente é par. Logo, o resultado é positivo:
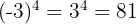
Escreva as seguintes expressões com potências positivas:
a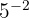
b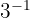
c
Observe que o expoente é negativo, portanto a expressão equivale ao inverso (recíproco) da base com expoente positivo:
a
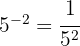
b
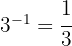
c
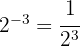
Escreva as seguintes expressões na forma de radicais:
a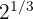
b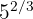
c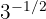
a O expoente é fracionário, então aplicamos a fórmula:
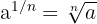
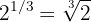
b O expoente também é fracionário. Aplicamos a fórmula:
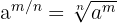
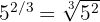
c Aqui o expoente é fracionário e negativo. Aplicamos a fórmula:
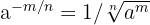
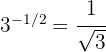
Escreva as seguintes raízes na forma de potências fracionárias:
a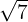
b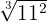
c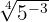
Para transformar uma raiz em potência fracionária, usamos a fórmula:
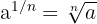
a
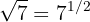
b
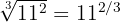
c
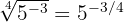
Escreva as seguintes operações como uma única potência, da forma: 
:
a 
b 
c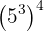 
d 
a Multiplicamos potências de mesma base somando os expoentes:
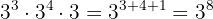
b Agora, dividimos as potências de mesma base subtraindo os expoentes:
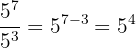
c Temos, agora, uma potência elevada a outra potência, portanto, multiplicamos os expoentes:
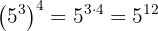
d Por termos três potências com o mesmo expoente, vamos multiplicar as bases:
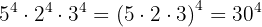
Escreva as seguintes operações como uma única potência, da forma: :
a 
b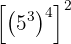 
c 
d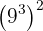 
a O primeiro caso se trata de potência elevada a outra potência, portanto, multiplicamos os expoentes:
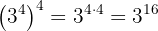
b Caso semelhante ao anterior. Potência elevada a outra e novamente a outra. Sendo assim, multiplicamos todos os expoentes::
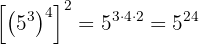
c Mais uma vez, potência elevada a outra potência:
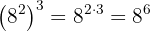
Mas como podemos observar: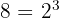 
. Assim, podemos simplificar ainda mais:
d Potência elevada a outra potência novamente. Como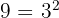 
, portanto,
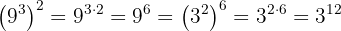
Escreva as seguintes operações como uma única potência, ou seja, na forma: :
a 
b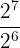 
c 
d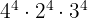 
a Temos uma multiplicação de potências com a mesma base. Portanto, somamos os expoentes:
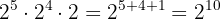
b Agora temos uma divisão de potências com a mesma base, então subtraímos os expoentes:
c Observamos que há uma potência elevada a outra potência. Nesse caso, os exponentes se soman:
d Temos, agora, multiplicação de potências com o mesmo expoente. Assim, podemos multiplicar as bases:
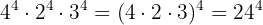
Escreva as seguintes operações como uma única potência, ou seja, na forma :
a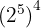 
b 
c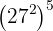 
d 
a Temos uma potência elevada a outra potência. Assim, multiplicamos os expoentes:
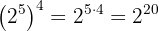
b Observamos que a potência está elevada ao expoente 0. Como,
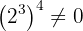
podemos concluir que,
c Temos novamente uma potência elevada a outra potência. Além disso,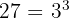 
d Mais uma vez, temos uma potência elevada a outra potência. Como,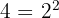 
:
temos,
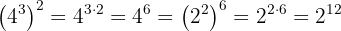
Resolva completamente as seguintes operações com potências:
a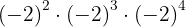 
b 
c 
d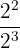 
a Podemos observar que temos multiplicação de potências com a mesma base. Assim, somamos os expoentes:
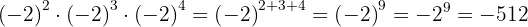
Retiramos o sinal porque o expoente é ímpar.
b Da mesma forma, temos multiplicação de potências com a mesma base:,
Mais uma vez, o sinal é negativo por se tratar de uma potência ímpar.
c Novamente, multiplicação de potências com a mesma base:
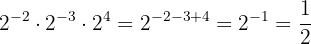
d Agora temos uma divisão de potências com a mesma base. Subtraímos os expoentes:
Resolva completamente as seguintes operações com potências:
a 
b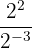 
c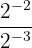 
a Temos uma divisão de potências com a mesma base:
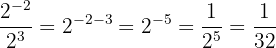
b Novamente, uma divisão de potências com a mesma base:
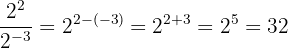
c Mais uma vez, divisão de potências com a mesma base:
Calcule as seguintes potências:
a 
b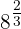 
c 
d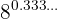 
Lembrando que os expoentes fracionários representam raízes.
a Podemos reescrever a expressão como:
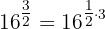
Usando a propriedade de multiplicação de expoentes:
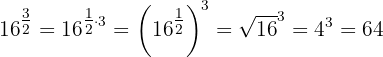
b Podemos escrever a expressão assim:
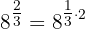
Se utilizamos a propriedade de multiplicação de exponentes:
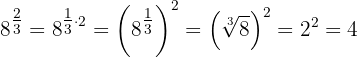
c Observamos que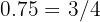 
. Portanto,
Logo,
d Agora o expoente é 
. Assim,
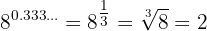
Simplifique a expressão:
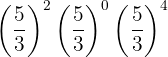
Devemos simplificar a seguinte expressão, que chamaremos de 
:
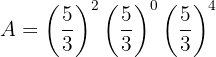
Começamos observando que, qualquer número elevado ao expoente 0, é igual a 1. Além disso, podemos utilizar a propriedade da multiplicação de potências de mesma base:
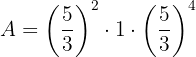
Em seguida, somamos os expoentes que possuem a mesma base:
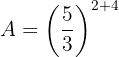
Ou seja,
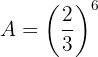
Simplifique a expressão:
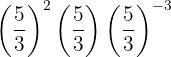
Devemos simplificar a seguinte expressão, que chamaremos de :
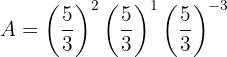
Podemos utilizar a propriedade da multiplicação de potências com a mesma base:
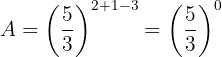
Aplicamos agora a propriedade que diz que qualquer número elevado ao expoente zero é igual a 1:
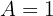
Simplifique a expressão:
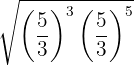
Devemos simplificar a seguinte expressão, que chamaremos de :
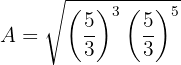
Podemos utilizar a propriedade da multiplicação de potências de mesma base:
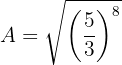
Em seguida, escrevemos a raiz em forma de potência fracionária:
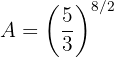
Ou seja,
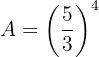
Simplifique a expressão:
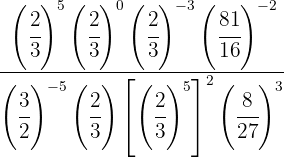
Devemos simplificar a seguinte expressão, que chamaremos de :
Começamos observando que qualquer número elevado ao expoente zero é igual a 1 (no numerador). Além disso, no denominador, podemos aplicar a propriedade da multiplicação de potências de mesma base:
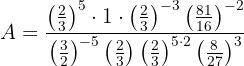
Depois, somamos os expoentes das potências que têm a mesma base:
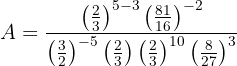
Ou seja,
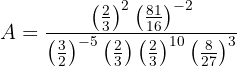
Agora transformamos as potências que têm expoentes negativos, tomando o recíproco da base:
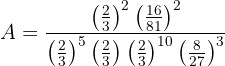
Mais uma vez, somamos e subtraímos os expoentes das potências com a mesma base:
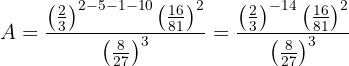
Agora, observamos que:
E que,
Portanto, a expressão se transforma em:
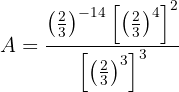
Aplicamos novamente a propriedade da multiplicação de potências:
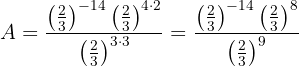
Somamos e subtraímos os expoentes:
Portanto, temos:
Gostou desse artigo? Deixe uma nota!
Loading...
