Nesta seção, aprenderemos a definição de monômio, suas características, propriedades e algumas operações entre eles.

O que é um monômio?
Monômio é uma expressão algébrica composta por apenas um termo, formado pelo produto de variáveis (ou incógnitas, chamadas de literais) elevadas a expoentes que são números inteiros não negativos, multiplicado por um número chamado de coeficiente. Por outro lado, um polinômio é a soma de vários monômios, então podemos entender um monômio como uma categoria de polinômio que consiste em apenas um termo.
O grau do monômio é o maior expoente entre as variáveis.
Exemplos de monômios são 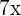 , em que a variável é
, em que a variável é  , seu coeficiente é
, seu coeficiente é  e seu grau é
e seu grau é  . Outro exemplo é
. Outro exemplo é 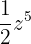 , em que a variável é
, em que a variável é  , seu coeficiente es
, seu coeficiente es  e seu grau é
e seu grau é  . Por fim, um último exemplo é
. Por fim, um último exemplo é 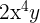 em que as incógnitas são
em que as incógnitas são  e
e  , o coeficiente é
, o coeficiente é  e seu grau é
e seu grau é  . Por outro lado,
. Por outro lado, 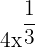 não é um monômio uma vez que seu expoente é uma fração, da mesma forma,
não é um monômio uma vez que seu expoente é uma fração, da mesma forma, 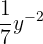 não é um monômio, pois seu expoente é negativo.
não é um monômio, pois seu expoente é negativo.
Identifique quais das seguintes expressões algébricas são monômios, e também indique qual é o seu grau e seu coeficiente.
1. 
2. 
3. 
4. 
5. 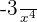
6. 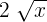
Vamos analisar as expressões para ver se atendem à definição de monômio. Se atenderem, então vamos identificar seu grau e coeficiente.
1. 
Podemos notar que cumpre com a definição de monômio. Além disso, dado que há apenas uma variável e seu expoente é  , assim, o grau do monômio é
, assim, o grau do monômio é  , além disso, seu coeficiente também é
, além disso, seu coeficiente também é  .
.
2. 
Podemos notar que a potência da variável  é
é  , e, portanto, a expressão não atende à definição de monômio, já que não podem ter expoentes negativos.
, e, portanto, a expressão não atende à definição de monômio, já que não podem ter expoentes negativos.
3. 
Não atende à definição de monômio, já que um monômio deve consistir em um único termo; aqui temos dois termos,  e
e  . Na verdade, isso é um binômio.
. Na verdade, isso é um binômio.
4. 
Atende à definição de monômio. Além disso, o grau é  uma vez que o exponente de
uma vez que o exponente de  é
é  . O coeficiente é
. O coeficiente é  .
.
5. 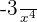
Não atende à definição de monômio, pois essa expressão é equivalente à 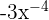 , cujo expoente é negativo.
, cujo expoente é negativo.
6. 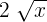
Não atende à definição de monômio, pois essa expressão é equivalente à 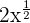 , e o expoente não é um número inteiro. Lembre-se de que o expoente deve ser um número inteiro não negativo.
, e o expoente não é um número inteiro. Lembre-se de que o expoente deve ser um número inteiro não negativo.
Operações básicas de monômios
Adição e subtração de monômios.
Para adicionar ou subtrair dois monômios e poder combinar os termos (simplificar), as variáveis presentes neles devem ser as mesmas e ter os mesmos expoentes. O resultado da adição ou subtração será um monômio cujo coeficiente será a soma ou diferença dos coeficientes sendo adicionados ou subtraídos, multiplicado pelas variáveis com seus respectivos expoentes. Por exemplo, a soma 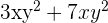 podem ser simplificadas, uma vez que as incógnitas ou variáveis são as mesmas,
podem ser simplificadas, uma vez que as incógnitas ou variáveis são as mesmas,  e
e  , além disso, elas tem as mesmas potências,
, além disso, elas tem as mesmas potências,  tem potência
tem potência  e
e  tem potência
tem potência  nos dois monômios, portanto o resultado seria igual a
nos dois monômios, portanto o resultado seria igual a
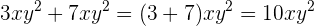
Por outro lado, a soma  não pode ser simplificado, já que os expoentes da incógnita
não pode ser simplificado, já que os expoentes da incógnita  não são iguais, portanto esta soma só pode ser expressa como
não são iguais, portanto esta soma só pode ser expressa como  . Ainda que seja possível isolar
. Ainda que seja possível isolar  de ambos monômios, esse não é um tópico que abordaremos neste artigo.
de ambos monômios, esse não é um tópico que abordaremos neste artigo.
Multiplicação e divisão de monômios
Entendemos que ao multiplicar dois termos com a mesma base, o resultado é a base elevada à soma dos expoentes. Em outras palavras, dadas as expressões com a mesma base  e
e  , seu produto é:
, seu produto é:
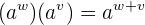
Desta forma, por exemplo, o resultado de  e
e 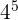 é:
é:
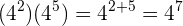
Com os monômios, é muito parecido. Dados dois monômios, ao multiplicá-los, o coeficiente resultante será o produto dos coeficientes respectivos e em relação às variáveis, simplesmente agrupamos aquelas com a mesma base e fazemos seus produtos respectivos. No caso de haver variáveis que apareçam em apenas um monômio, e não no outro, então as transferimos diretamente. Assim, por exemplo, vamos considerar os monômios  e
e 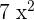 , assim seu resultado é:
, assim seu resultado é:

Da mesma forma, sabemos que ao dividir dois termos com a mesma base, o resultado é a base elevada à diferença dos expoentes (o expoente do numerador menos o expoente do denominador). Em outras palavras, dadas as expressões com a mesma base  e
e  , a divisão é:
, a divisão é:
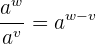
Dessa maneira, por exemplo, o resultado de  e
e 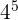 é:
é:

Com os monômios, é muito parecido. Dados dois monômios, ao fazer sua divisão, o coeficiente resultante será a divisão dos respectivos coeficientes, e em relação às variáveis, simplesmente agrupamos aquelas com a mesma base e fazemos suas respectivas divisões. No caso de haver variáveis no numerador que não estejam no denominador, então as transferimos diretamente. No entanto, se houver variáveis no denominador que não estejam no numerador, então as transferimos, mas mudando o sinal do expoente. Assim, por exemplo, vamos considerar os monômios  e
e 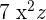 , então, sua divisão é:
, então, sua divisão é:
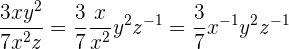
Potências de monômios
A potência dos monômios é simples. Basta elevar tanto o coeficiente quanto cada literal à potência à qual elevamos todo o monômio. Claro, sempre aplicando as propriedades do expoente. Portanto, se quisermos elevar, por exemplo, o monômio  á potência
á potência  , temos que:
, temos que:

Exercícios sobre operações com monômios
Exercícios de adição e subtração de monômios
1. 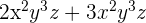
2. 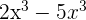
3. 
4. 
Para resolver esses exercícios, vamos utilizar a explicação sobre soma e subtração de monômios que vimos anteriormente.
1. 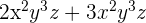
Como ambos monômios têm as mesmas variáveis e elas têm as mesmas potências, podemos simplificar diretamente.
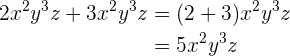
2. 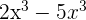
Como ambos monômios têm as mesmas variáveis e elas têm as mesmas potências, podemos simplificar diretamente.
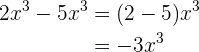
3. 
Podemos observar que todos os monômios têm as mesmas variáveis, porém apenas dois monômios têm variáveis com as mesmas potências. Portanto, apenas esses dois podem ser simplificados
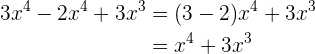
4. 
Vamos observar que todos os monômios têm as mesmas variáveis, porém nem todos têm essas variáveis elevadas às mesmas potências. Vamos agrupar os monômios que tenham as mesmas variáveis com as mesmas potências e assim simplificamos
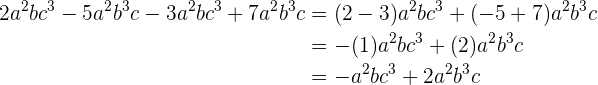
Exercícios de produtos de monômios
1. 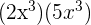
2. 
3. 
4. 
5. 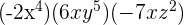
Para resolver esses exercícios, vamos usar a explicação sobre produtos de monômios que vimos anteriormente. Vamos lembrar de agrupar variáveis iguais e coeficientes.
1. 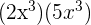
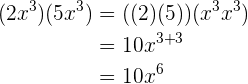
2. 
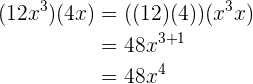
3. 
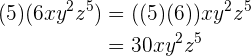
4. 
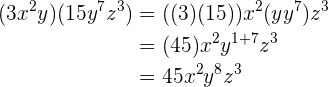
5. 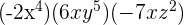
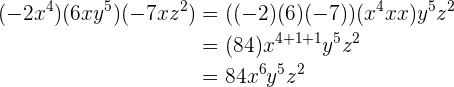
Exercícios de divisão de monômios
1. 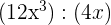
2. 
3. 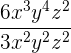
4. 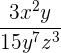
5. 
Para resolver esses exercícios, vamos usar a explicação sobre divisão de monômios que vimos anteriormente. Vamos lembrar de agrupar variáveis iguais e coeficientes..
1. 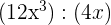
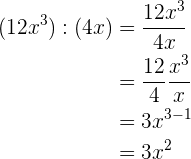
2. 
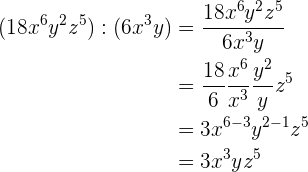
3. 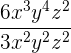
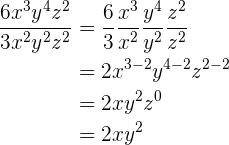
4. 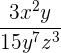
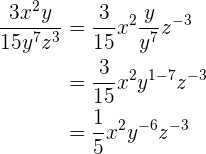
5. 
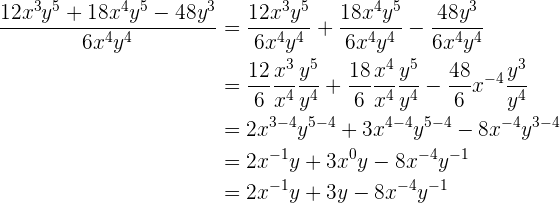
Exercícios de potências de monômios
1. 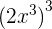
2. 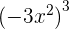
3. 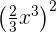
Para resolver esses exercícios, vamos usar a explicação sobre potências de monômios que vimos anteriormente. Vamos lembrar de elevar tanto as variáveis quanto os coeficientes a essa potência.
1. 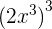
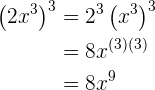
2. 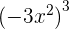
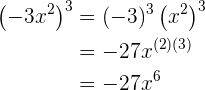
3. 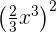
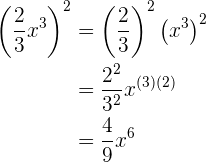
Resumir com IA:













