Binômio ao quadrado
Um binômio ao quadrado é igual ao quadrado do primeiro, mais o dobro do primeiro pelo segundo, mais o quadrado do segundo.
Se os dois sinais do binômio são iguais, o dobro do primeiro pelo segundo é positivo.
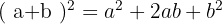
Se os sinais do binômio são diferentes, o dobro do primeiro pelo segundo é negativo.
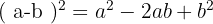
Exemplos de exercícios com binômios ao quadrado
1.
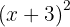
Para resolver este caso usamos a primeira fórmula com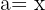 
e 
, substituímos, ficando assim
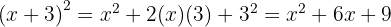
2.
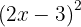
Para resolver este caso usamos a segunda fórmula com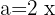 
e , substituímos, ficando assim
3.
Para resolver este caso usamos a primeira fórmula com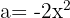 
e , substituímos, ficando assim
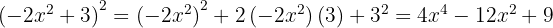
4.
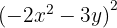
Para resolver este caso usamos a primeira fórmula com 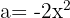e 
, substituímos, ficando assim
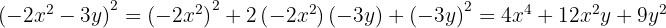
Soma pela diferença
Uma soma pela diferença é igual à diferença de quadrados.
Exemplos de exercícios com soma pela diferença
1.
Usando a fórmula, vamos chamar 
e 
, então substituímos, ficando assim
e , então substituímos, ficando assim
2.
Usando a fórmula vamos chamar 
e 
, então substituímos, ficando assim
Binômio ao cubo
Um binômio ao cubo é igual ao cubo do primeiro termo, mais o triplo do quadrado do primeiro pelo segundo, mais o triplo do primeiro pelo quadrado do segundo, mais o cubo do segundo.
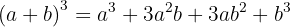
Aconselhamos que aprenda esta fórmula.
Exemplos de exercícios com binômios ao cubo
1.
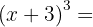
Usando a fórmula vamos chamar 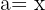e , então substituímos, ficando assim
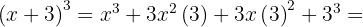
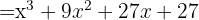
2.
Usando a fórmula vamos chamar 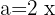e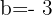 
, então substituímos, ficando assim
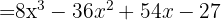
Se nos atentamos nos sinais obtidos: +, −, +, −. Podemos dar uma variante para a fórmula anterior:
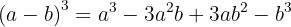
3.
Usando a fórmula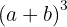 
vamos chamar 
e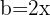 
, substituímos, ficando assim
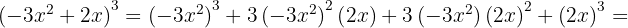
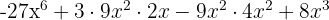
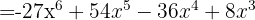
Os sinais obtidos são: −, +, −, +. Podemos dar outra variante:
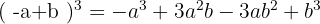
4.
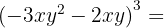
Usando a fórmula 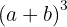vamos chamar 
e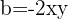 
, então substituímos, ficando assim
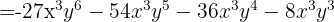
Os sinais obtidos são: −, −, −, −. Podemos dar outra variante:
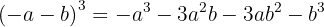
Trinômio ao quadrado
Um trinômio ao quadrado é igual ao quadrado do primeiro termo, mais o quadrado do segundo, mais o quadrado do terceiro, mais o dobro do produto do primeiro pelo segundo, mais o dobro do produto do primeiro pelo terceiro, mais o dobro do produto do segundo pelo terceiro.
Exemplos de exercícios com trinômios ao quadrado
1.
Para resolver este exercício usamos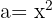 
, 
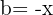e 
, substituímos na fórmula, ficando assim
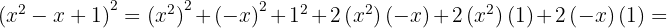
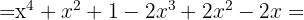
2.
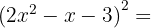
Para resolver este exercício usamos , 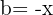e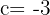 
, substituímos na fórmula, ficando assim
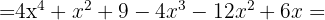
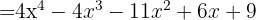
Soma de cubos
Agora em vez de trabalhar as expressões, o que faremos será fatorar, ou seja, escrevê-las como o produto de outras duas expressões.
A fórmula que utilizamos para fatorar a soma de cubos é a seguinte:
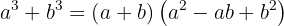
Exemplo de exercícios com soma de cubos
Fatore a seguinte expressão:
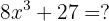
Primeiro, devemos observar como podemos reescrever os términos para usarmos a fórmula de fatoração de cubos. Neste caso, podemos reescrever a expressão da seguinte maneira:
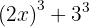
Utilizando a fórmula de cubos e considerando que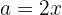 
e 
, temos:
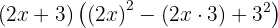
Calculando, temos:
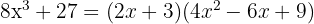
Diferença de cubos
A fórmula para calcular diferença de cubos tem a seguinte estrutura:
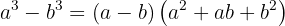
Exemplo de exercício com diferença de cubos
Fatore a seguinte expressão:
Igual que antes, é importante primeiro observar para entender como podemos reescrever os términos para usar a fórmula de fatoração de cubos. Neste caso, podemos reescrever a expressão da seguinte maneira:
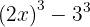
Utilizando a fórmula de cubos e considerando qu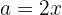e e
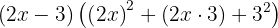
Calculando, temos:
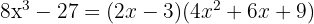
Produto de dois binômios que tem um término comum
Quando apresentamos o produto de dois binômios com término comum, o cálculo é mais simples, que fica da seguinte maneira:
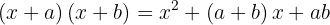
Exemplo de exercício com produto de dois binômios com término comum
Calcule a seguinte expressão:
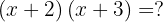
Não é preciso lembrar a fórmula. Seguindo os passos do cálculo e fazendo atenção aos sinais, podemos simplesmente fazer o passo a passo.
Primeiro, pegamos os termos dentro do primeiro parêntese e multiplicamos com os segundos, desta maneira:
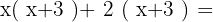
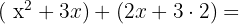
Recomendamos manter os parênteses e se desfazer deles depois. Assim, vamos nos assegurar de não trocar acidentalmente os sinais de + por - ou ao revés. Neste caso, não há nenhuma mudança de sinal.
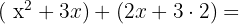
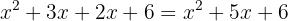
Exemplos de exercícios resolvidos de produtos notáveis
Calcule os binômios ao quadrado:
1.
Usamos a fórmula 
, onde 
e 
, substituímos, ficando assim
2.
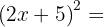
Usamos a fórmula , onde 
e , substituímos, ficando assim
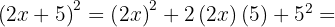
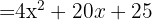
3.
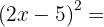
Usamos a fórmula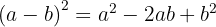 
, onde e , substituímos, ficando assim
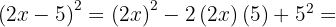
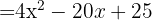
4.
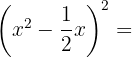
Usamos a fórmula 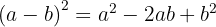, onde 
e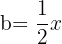 
, substituímos, ficando assim
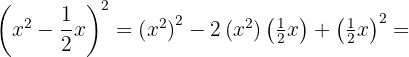
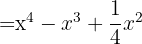
Calcule os binômios ao cubo.
1.
Usamos a fórmula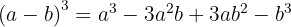 
, onde e 
, substituindo, fica assim
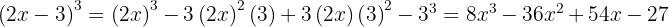
2.
Usamos a fórmula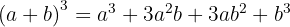 
, onde e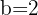 
, substituindo, fica assim
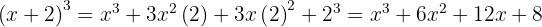
3.
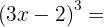
Usamos a fórmula 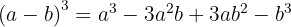, ond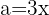e 
e 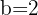, substituindo, fica assim
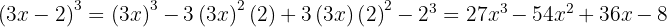
4.
Usamos a fórmula 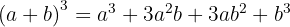, onde e , substituindo, fica assim
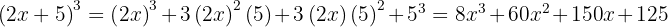
Calcule a soma pela diferença
1.
Usamos a fórmula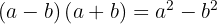 
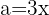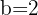, onde e , substituindo, fica assim
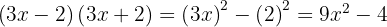
2.
Usamos a fórmula 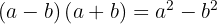, onde e , substituindo, fica assim
3.
Usamos a fórmula 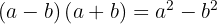, onde 
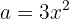e 
, substituindo, fica assim
4.
Usamos a fórmula 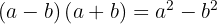, onde 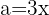e , substituindo, fica assim
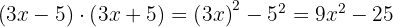
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
