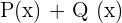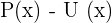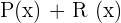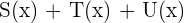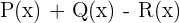Temas
- Analise se as seguintes expressões algébricas são polinômios ou não.
- Escreva em linguagem matemática
- Dados os polinômios, P,Q,R,U e as expressões algébricas S,T:
- Dados os polinômios, P,Q,R:
- Faça as seguintes multiplicações
- Faça as seguintes divisões:
- Divida utilizando a regra de Ruffini
- Sem efetuar as divisões, encontre o resto das seguintes operações:
- Indique quais dessas divisões são exatas:
- Comprove que os seguintes polinômios têm os fatores indicados:
- Comprove que os seguintes polinômios têm os fatores indicados:
- Comprove que os seguintes polinômios têm os fatores indicados:
- Calcule os valores indicados:
- Calcule os valores indicados:
- Calcule os coeficientes indicados:
- Calcule o valor de k:
- Encontre o polinômio que cumpra o seguinte:
- Calcule o valor de a:
Exercícios resolvidos de grau e termo independente de polinômio, polinômios ordenados, somas e subtração de polinômios, multiplicação de polinômios, divisão de polinômios, divisão por Ruffini, teorema do resto, resto de um polinômio e teorema do fator.

Analise se as seguintes expressões algébricas são polinômios ou não.
Em caso afirmativo, indique qual é seu grau e termo independente.
Analise se as seguintes expressões algébricas são polinômios ou não. Em caso afirmativo, indique qual é seu grau e termo independente.
a) 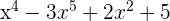
Grau:  , termo independente:
, termo independente:  .
.
b) 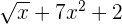
Não é um polinômio porque a parte literal do primeiro monômio está dentro de uma raiz.
c) 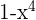
Grau:  , termo independente:
, termo independente:  .
.
d) 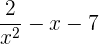
Não é um polinômio porque o expoente  do primeiro monômio não é um número natural.
do primeiro monômio não é um número natural.
e) 
Grau:  , termo independente:
, termo independente: .
.
f) 
Não é um polinômio porque o expoente do segundo monômio não é um número natural.
g) 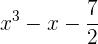
Grau:  , termo independente:
, termo independente: 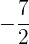 .
.
Escreva em linguagem matemática
- Um polinômio ordenado sem termo independente.
- Um polinômio não ordenado e completo.
- Um polinômio completo sem termo independente.
- Um polinômio de grau
 , completo e com coeficientes ímpares.
, completo e com coeficientes ímpares.
Escreva:
a) Um polinômio ordenado sem termo independente.
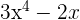
b) Um polinômio não ordenado e completo.
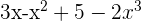
c) Um polinômio completo sem termo independente.
Impossível
d) Um polinômio de grau  , completo e com coeficientes ímpares.
, completo e com coeficientes ímpares.

Dados os polinômios, P,Q,R,U e as expressões algébricas S,T:
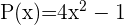
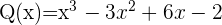
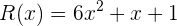
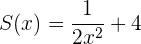
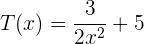

Calcule:
Dados os polinômios e as expressões algébricas:
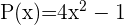
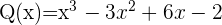
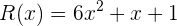
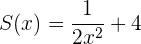
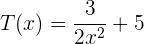

Calcule:
a) 
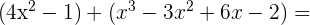
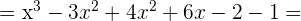
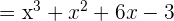
b) 
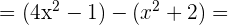


c) 
= 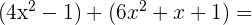
= 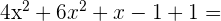
= 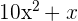
d) 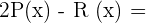
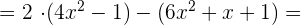


e) 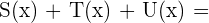
= 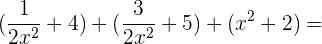
= 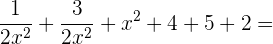
= 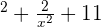
f) 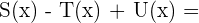
= 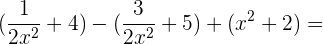
= 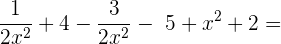
= 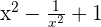
Dados os polinômios, P,Q,R:
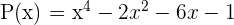


Calcule:
Dados os polinômios:
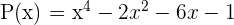

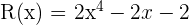
Calcule:
a) 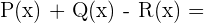

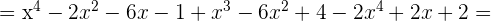


b) 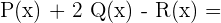
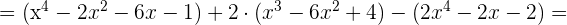

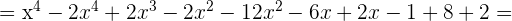
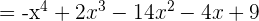
c) 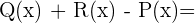

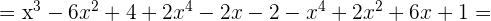
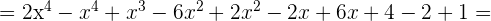
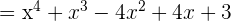
Faça as seguintes multiplicações
- 1
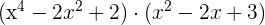
- 2
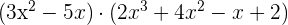
- 3
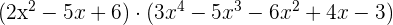
Faça as seguintes multiplicações
a) 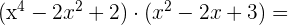
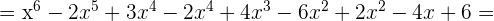
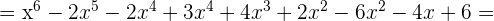
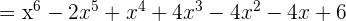
b) 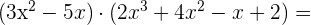
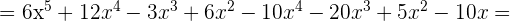
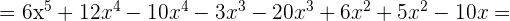

c) 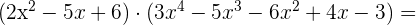
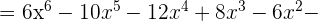
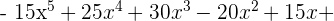
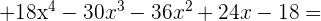

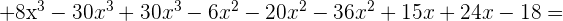
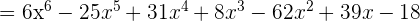
Faça as seguintes divisões:
-
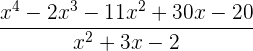
-
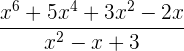
- Dados os polinômios:
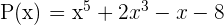

Resolva:
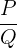
Faça as seguintes divisões:
a. 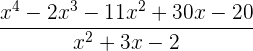
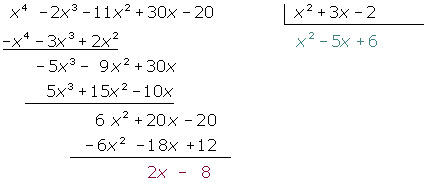
b. 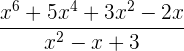
c. Dados os polinômios:
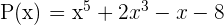

Resolva:
 :
:
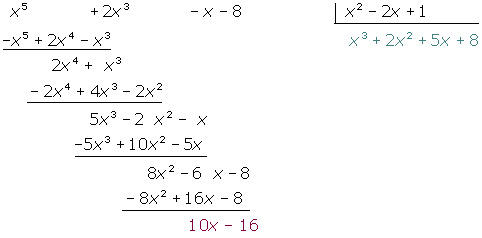
Divida utilizando a regra de Ruffini
Divida por Ruffini:
a) 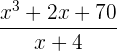
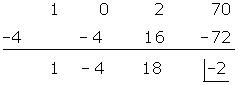
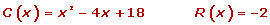
b) 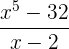
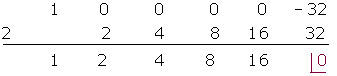
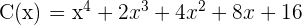
c) 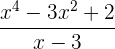
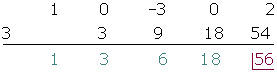
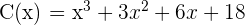
Sem efetuar as divisões, encontre o resto das seguintes operações:
Sem efetuar as divisões, encontre o resto das seguintes operações:
Para encontrar o resto usaremos o teorema do resto que nos diz que o resto da divisão de um polinômio  , entre um polinômio da forma
, entre um polinômio da forma  é o valor numérico de tal polinômio para o valor:
é o valor numérico de tal polinômio para o valor: 
a. 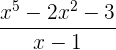
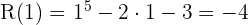
b. 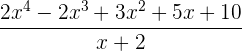
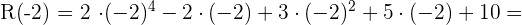
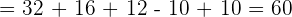
c. 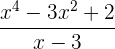
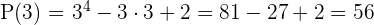
Indique quais dessas divisões são exatas:
Indique quais dessas divisões são exatas:
a) Aplicamos o teorema do resto. Se o resto é zero a divisão será exata.
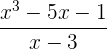

Não é exata.
b) 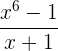
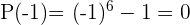
Exata.
c) 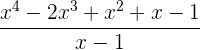
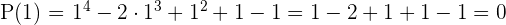
Exata.
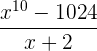
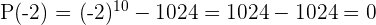
Exata.
Comprove que os seguintes polinômios têm os fatores indicados:
-
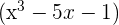 tem por fator
tem por fator 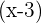
-
 tem por fator
tem por fator 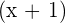
-
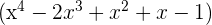 tem por fator
tem por fator 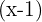
 tem por fator
tem por fator 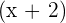
a. 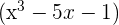 tem por fator
tem por fator 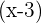
b.  tem por fator
tem por fator 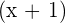
c. 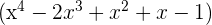 tem por fator
tem por fator 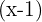
d.  tem por fator
tem por fator 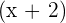
Comprove que os seguintes polinômios têm os fatores indicados:
-
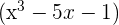 tem por fator
tem por fator 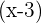
-
 tem por fator
tem por fator 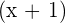
-
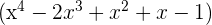 tem por fator
tem por fator 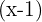
-
 tem por fator
tem por fator 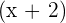
Comprove que os seguintes polinômios têm os fatores indicados:
a. 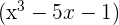 tem por fator
tem por fator 
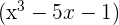 é divisível por
é divisível por  se e apenas se
se e apenas se  .
.

 não é um fator.
não é um fator.
b. 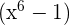 tem por fator
tem por fator 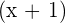
 é divisível por
é divisível por 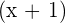 se e apenas se
se e apenas se 
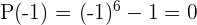
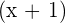 é um fator.
é um fator.
c. 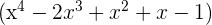 tem por fator
tem por fator 
 .
.
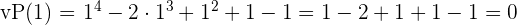
 é um fator.
é um fator.
d. 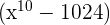 tem por fator
tem por fator 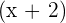
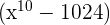 é divisível por
é divisível por 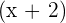 se e apenas se
se e apenas se  .
.
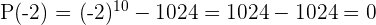
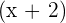 é um fator.
é um fator.
Comprove que os seguintes polinômios têm os fatores indicados:
-
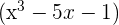 tem por fator
tem por fator 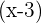
-
 tem por fator
tem por fator 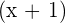
-
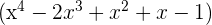 tem por fator
tem por fator 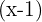
-
 tem por fator
tem por fator 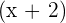
Comprove que os seguintes polinômios têm os fatores indicados:
a. 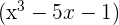 tem por fator
tem por fator 
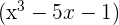 é divisível por
é divisível por  se e apenas se
se e apenas se  .
.

 não é um fator.
não é um fator.
b. 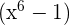 tem por fator
tem por fator 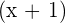
 é divisível por
é divisível por 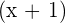 se e apenas se
se e apenas se 
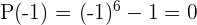
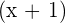 é um fator.
é um fator.
c. 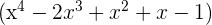 tem por fator
tem por fator 
 .
.
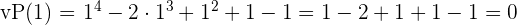
 é um fator.
é um fator.
d. 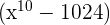 tem por fator
tem por fator 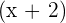
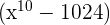 é divisível por
é divisível por 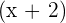 se e apenas se
se e apenas se  .
.
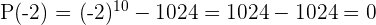
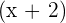 é um fator.
é um fator.
Calcule os valores indicados:
Encontre  e
e  para que o polinômio
para que o polinômio 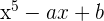 seja divisível por
seja divisível por 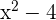 .
.
Encontre  e
e  para que o polinômio
para que o polinômio 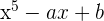 seja divisível por
seja divisível por 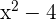 .
.
Decompomos em fatores a diferença de quadrados
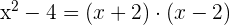
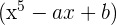 é divisível por
é divisível por  se e apenas se
se e apenas se  y
y 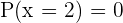
Aplicamos o teorema do resto sabendo que o resto é zero
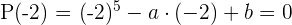
Operamos


Aplicamos o teorema do resto sabendo que o resto é zero
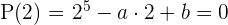
Operamos
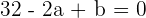

Obtemos duas equações com duas incógnitas. Resolveremos o sistema por redução:
Calcule os valores indicados:
Encontre  e
e  para que o polinômio
para que o polinômio 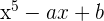 seja divisível por
seja divisível por 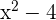 .
.
Encontre  e
e  para que o polinômio
para que o polinômio 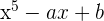 seja divisível por
seja divisível por 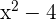 .
.
Decompomos em fatores a diferença de quadrados
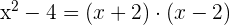
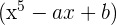 é divisível por
é divisível por  se e apenas se
se e apenas se  y
y 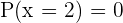
Aplicamos o teorema do resto sabendo que o resto é zero
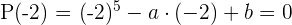
Operamos


Aplicamos o teorema do resto sabendo que o resto é zero
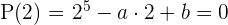
Operamos
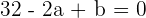

Obtemos duas equações com duas incógnitas. Resolveremos o sistema por redução
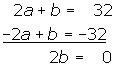

Calcule os coeficientes indicados:
Determine os coeficientes de  e
e  para que o polinômio
para que o polinômio 
seja divisível por 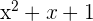 .
.
Determine os coeficientes de  e
e  para que o polinômio
para que o polinômio 
seja divisível por 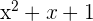 .
.
Efetuamos a divisão
Para que seja divisível a divisão têm que ser exata, isto é,
o resto tem que ser zero.
Para que o resto seja zero o coeficiente da  e o coeficiente do termo independente têm que ser zero
e o coeficiente do termo independente têm que ser zero
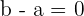
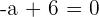


Calcule o valor de k:
Encontre o valor de  para que ao dividir
para que ao dividir 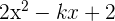 por
por 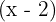 dê
dê  como resto.
como resto.
Encontre o valor de  para que ao dividir
para que ao dividir 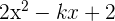 por
por 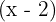 dê
dê  como resto.
como resto.
Aplicamos o teorema do resto e sabemos que o resto é 
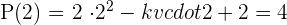
Operamos
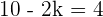
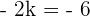

Encontre o polinômio que cumpra o seguinte:
Encontre um polinômio de quarto grau que seja divisível por 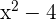
e se anule para  e
e  .
.
Encontre um polinômio de quarto grau que seja divisível por 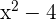 e se anule para
e se anule para 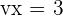 e
e  .
.
Se se anula para  e
e  , então
, então  e
e 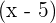 são fatores do polinômio que procuramos
são fatores do polinômio que procuramos 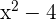 é outro fator, já que o polinômio é divisível por
é outro fator, já que o polinômio é divisível por 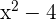
Multiplicamos os fatores:
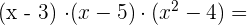
Em primeiro lugar multiplicamos os dois primeiros
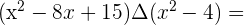
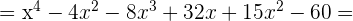
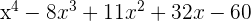
Calcule o valor de a:
Calcule o valor de a para que o polinômio 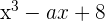 tenha raiz
tenha raiz  ,
,
e calcule outras raízes.
Calcule o valor de a para que o polinômio 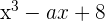 tenha raiz
tenha raiz  ,
,
e calcule outras raízes.
Calculamos o valor de  sabendo que o valor numérico do polinômio para
sabendo que o valor numérico do polinômio para  tem que ser zero
tem que ser zero
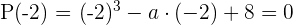

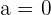
Fatoramos dividindo por Ruffini
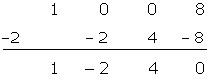

Igualamos o segundo fator a zero e resolvemos a equação do segundo grau 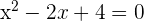
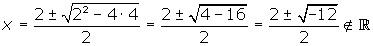
Não tem mais raízes reais.
Resumir com IA: