Temas
Método de substituição
O método de integração por mudança de variável ou substituição se baseia na derivada da função composta.
Para mudar a variável identificamos uma parte do que será integrado com uma nova variável t, de modo que se obtenha uma integral mais simples.
Passos para integrar por mudança de variável
1 É feita a substituição de variável e então diferencia-se nos dois termos:
2Substitui-se a diferencial na integral.
3 Se a integral resultante for mais simples, vamos fazer a integração:
4 Retorna a variável original:
Exemplo: Resolva usando integração por substituição, a integral
1 Realizamos a substituição de variável
Calculamos a diferencial
2Substituímos na integral e o simplificamos, integrando
3Resolvemos a nova integral
4Voltamos com a variável original, para tal, vamos usar 
Assim, a solução obtida é
Substituições de variáveis comuns
Aqui estão algumas das substituições de variáveis comuns usadas para resolver integrais.
1 
2 
3 
4 
5 Nas funções racionais de raízes com índices diferentes, do mesmo radicando linear 
, a substituição de variável é 
elevado ao mínimo comum múltiplo dos índices.
6 Se 
é par:
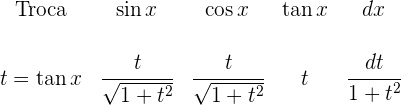
7 Se 
não é par:
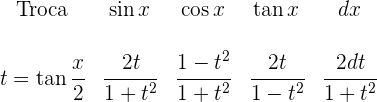
Exercícios propostos
Resolva as seguintes integrais, usando o método de substituição.
a) Realizamos a substituição de variável e calculamos sua diferencial
b) Substituímos na integral e, para simplificar, usamos identidades trigonométricas
c) Resolvemos as integrais obtidas
d) Voltamos à variável original, para isso resolvemos na substituição de variável
Calculamos para o seno e cosseno de
Dessa forma, o resultado se expressa na variável 
como
a) Realizamos a substituição de variável e calculamos sua diferencial
b) Substituímos na integral e simplificamos
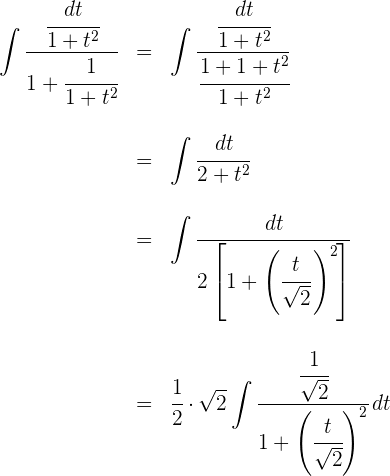
c) Resolvemos as integrais obtidas
d) Voltamos à variável original
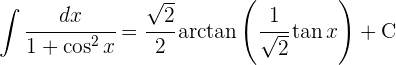
a) Realizamos a substituição de variável e calculamos sua diferencial
b) Substituímos na integral e fazemos a simplificação
c) Resolvemos as integrais obtidas
d) Voltamos à variável original
a) Realizamos a substituição da variável e calculamos sua diferencial
b) Substituímos na integral e fazemos a simplificação
c) Resolvemos as integrais obtidas
d) Voltamos à variável original.
Dessa forma, a solução em termos da variável original é
a) Realizamos a substituição de variável e calculamos sua diferencial
b) Substituímos na integral e simplificamos
c) Resolvemos as integrais obtidas
d) Voltamos à variável original
Assim, a solução em termos da variável original é
a) Realizamos a substituição de variável e calculamos sua diferencial
b) Substituímos na integral e simplificamos
c) Resolvemos as integrais obtidas
d) Voltamos à variável original
Dessa forma, a solução em termos da variável original é
Gostou desse artigo? Deixe uma nota!
Loading...
