Temas
Métodos para a obtenção das raízes e fatoração
Na equação da forma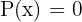 
, o polinômio 
ode ser decomposto em fatores de primeiro e segundo grau. Para isso utilizaremos o teorema do resto e a regra de Ruffini. Também será útil a fórmula geral.
Como estão relacionadas as raízes do polinômio com sua fatoração?
Se tenho um polinômio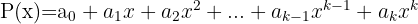 
de grau 
com raízes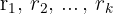 
,então o polinômio se fatora como:
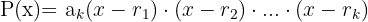
Exemplo
1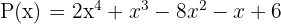 
Solução
Tomamos os divisores do termo independente: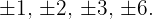 
Aplicando o teorema do resto saberemos para quais desses valores a divisão é exata. Começamos com 1..
Como resultou 0, a divisão de pelo fator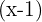 
é exata, assim que procedemos a calculá-la por Ruffini.
Dividimos por Ruffini.
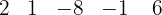
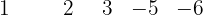
Por ser a divisão exata, D = d · c, então:
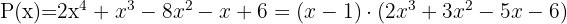
Concluímos que uma raiz do polinômio é 
.
Continuamos realizando as mesmas operações com o segundo fator.
Voltamos a testar novamente com 1 porque o primeiro fator poderia estar elevado ao quadrado. Para isso usamos o quociente resultante de Ruffini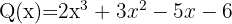 
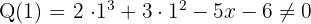
Como resultou um número diferente de 0, testamos outro divisor, por exemplo -1
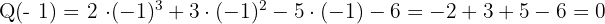
Como é igual a 0, calculamos a divisão de 
por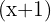 
com Ruffini.
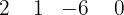
Concluímos então que,
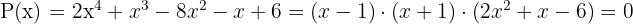
Outra raiz é 
.
Como já nos resta encontrar as raízes de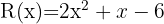 
e é um polinômio de segundo grau, podemos usar a fórmula geral. Também poderíamos continuar como temos feito, porém esse método só encontra raízes inteiras e não serviria se o polinômio tivesse raízes não inteiras.
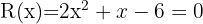
Usando a fórmula geral temos que:
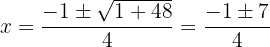
Então,
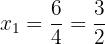
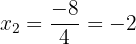
As soluções são: , 
, 
e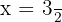 
A partir disso, se conclui que o polinômio pode ser fatorizado como:
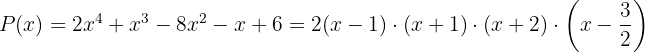
Exercícios propostos para a resolução de equações pelo método de Ruffini e pelo teorema do resto
Tomamos os divisores do termo independente: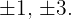 
Aplicando o teorema do resto saberemos para quais desses valores a divisão é exata. Começamos com 1.
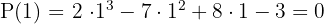
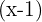Como o resultado foi 0, a divisão de pelo fator é exata, então procedemos ao cálculo pelo método de Ruffini.
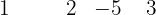
Então:
Conclui-se que uma raiz do polinômio é .
Continuamos realizando as mesmas operações no segundo fator.
Testamos novamente com 1 porque essa raiz pode se repetir, ou seja, o primeiro fator poderia estar elevado ao quadrado. Para isso, usamos o quociente obtido em Ruffini 
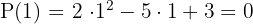
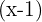Como o resultado foi 0, calculamos a divisão de por com Ruffini.
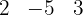
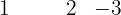
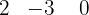Portanto,
As soluções são: 
e
Disso se conclui que o polinômio se fatoriza como:
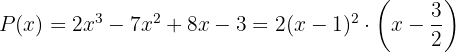
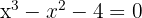
Tomamos os divisores do termo independente: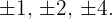 
Aplicando o teorema do resto saberemos para quais desses valores a divisão é exata
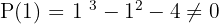
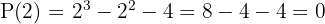
Como o resultado foi 0, a divisão de por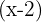 
é exata, então procedemos ao cálculo por Ruffini.
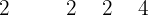
Portanto,
Como resta encontrar as raízes de 
e trata-se de um polinômio do segundo grau, aplicamos a fórmula geral.
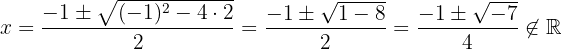
Como não resulta em número real, não podemos decompor mais o polinômio do 2º grau, então o polinômio é fatorizado assim:
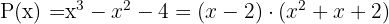
E possui apenas uma raiz real: 
Tomamos os divisores do termo independente: 
.
Aplicando o teorema do resto verificamos para quais desses valores a divisão é exata.
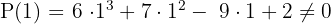
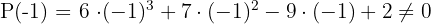
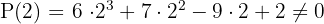
Como o resultado foi 0 neste último, a divisão de por 
é exata, então fazemos o cálculo por Ruffini.
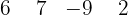
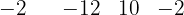
Então,
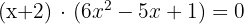
Como temos que encontrar as raízes de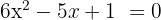 
e é um polinômio de segundo grau usamos a fórmula geral:
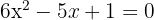
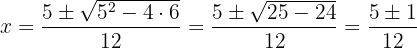
Portanto,
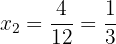
As soluções são: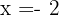 
, 
y 
Assim, o polinômio é fatorizado como:
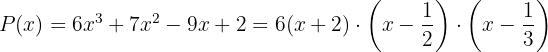
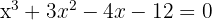
Tomamos os divisores do termo independente: 
Aplicando o teorema do resto verificamos para quais desses valores a divisão é exata.
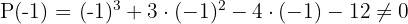
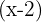Como o resultado foi 0, a divisão de por é exata, então fazemos o cálculo pelo método de Ruffini.
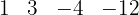
Então,
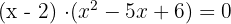
Agora, vamos encontrar as raízes do segundo fator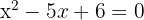 
e é um polinômio de segundo grau, usamos a fórmula geral:
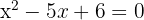
Portanto:
As soluções são: , , 
.
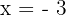Assim, o polinômio se fatoriza como:
Gostou desse artigo? Deixe uma nota!
Loading...
