Quando falamos em fatorar polinômios, há várias características que precisamos observar.
Se não há termo independente:
Se não há termo independente, é necessário colocar o fator comum em evidência. Colocar o fator comum em evidência em uma soma (ou subtração) consiste em transformá-la em um produto.
Aplicamos a propriedade distributiva:
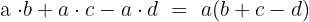
Exemplo de fatoração de polinômio sem termo independente
Decomposição em fatores, colocando o fator comum em evidência, e encontrar as raízes..
1. 
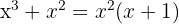
As raízes são: 
e 
2. 
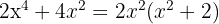
Só existe uma raiz porque o polinômio 
não tem nenhum valor que o anule. Como 
está elevado ao quadrado, o resultado sempre será um número positivo, portanto, é irredutível.
Dupla fatoração por fator comum
1. 
Colocando o fator comum em evidência: e 
.
Como 
é agora um fator comum, colocamos o fator comum em evidência .
As raízes são: 
e 
.
Se temos um binômio
Quando temos um binômio, pode ocorrer um dos seguintes casos:
Diferença de quadrados
A diferença de quadrados é igual ao produto da soma pela diferença.
Exemplos de exercícios com diferença de quadrados:
Faça a fatoração e encontre as raízes:
1. 
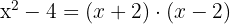
As raízes são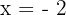 
e 
2. 
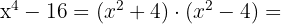
O último termo também é uma diferença de quadrados, então:
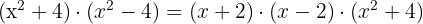
As raízes são: 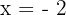e
Soma de cubos
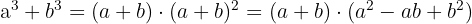
Exemplo de exercício com soma de cubos:
Diferença de cubos
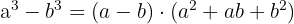
Exemplo de exercício com diferença de cubos :
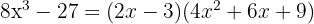
Se temos um trinômio
Quando temos um trinômio, pode acontecer um dos seguintes casos:
Trinômio quadrado perfeito
Um trinômio quadrado perfeito é igual a um binômio ao quadrado.
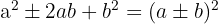
Exemplos de trinômios quadrados perfeitos
Faça a fatoração e descubra as raízes:
1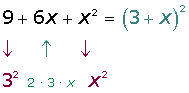 
Vamos fazer as perguntas:
- Qual número elevado ao quadrado é igual a
? A resposta é 
. - Qual número elevado ao quadrado é igual a
? A resposta é .
E precisamos verificar se o resultado satisfaz a equação: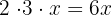 
A raiz é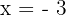 
, e portanto, trata-se de uma raiz dupla.
2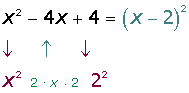 
- Qual número elevado ao quadrado é igual a ?
- Qual número elevado ao quadrado é igual a
? 
E precisamos verificar se o resultado satisfaz a equação: 
A raiz dupla é .
Trinômio de segundo grau
Para fatorar um trinômio de segundo grau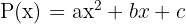 
, igualamos a zero e resolvemos a equação de segundo grau.
Se os resultados da equação são: 
e 
, o polinômio fatorado será:
Exemplos de trinômios de segundo grau
Efetue a fatoração e encontre as raízes
1. 
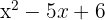
Vamos igualar o trinômio a zero:
Aplicamos a fórmula da equação de segundo grau:
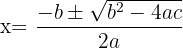
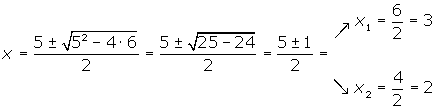
Fazemos a fatoração:
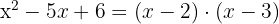
As raízes são 
e 
.
2. 
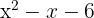
Igualamos o trinômio a zero:
Resolvemos a equação:
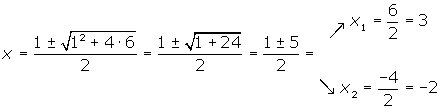
Fatoramos:
E as raízes são e 
.
Trinômios de quarto grau de expoentes pares
Para encontrar as raízes, igualamos a zero e resolvemos a equação biquadrada.
Exemplos de trinômios de quarto grau com expoentes pares
1. 
Igualamos o polinômio a zero
Realizamos uma mudança de variável
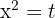
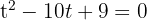
Resolvemos a equação de segundo grau
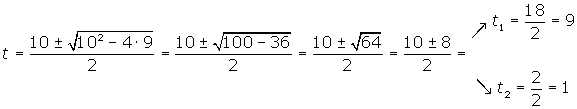
Desfazemos a mudança de variável e obtemos as raízes.
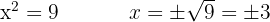
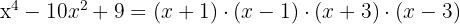
2. 
Igualamos o polinômio a zero
Realizamos uma mudança de variável
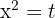
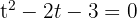
Resolvemos a equação de segundo grau
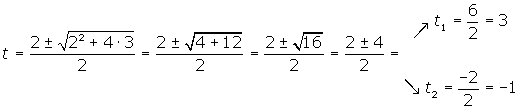
Desfazemos a mudança de variável e obtemos as raízes.
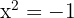, não tem raízes reais uma vez que não existe nenhum número que, elevado ao quadrado, seja negativo.
Será fatorado como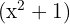 
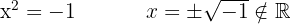
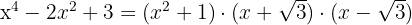
Fatoração de um polinômio de grau superior a dois
Utilizamos o Teorema do Resto e a Regra de Ruffini para encontrar as raízes inteiras.
Os passos a seguir serão demonstrados com o polinômio:
Usamos os divisores do termo independente: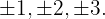 
Aplicando o Teorema do Resto, saberemos para quais valores a divisão é exata.
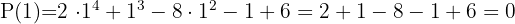
Dividimos por Ruffini.
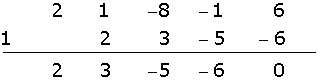
Por ser uma divisão exata, 
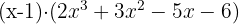
Uma raiz é 
.
Continuamos realizando as mesmas contas para encontrar o segundo fator.
Voltamos a testar por 
porque o primeiro fator pode estar elevado ao quadrado.
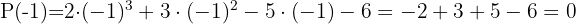
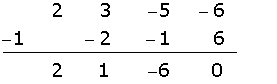
A outra raiz é .
O terceiro fator pode ser encontrado aplicando a equação do segundo grau ou do mesmo modo que temos feito, embora tenha a desvantagem de que só podemos encontrar raízes inteiras.
Descartamos o e continuamos testando por 
..
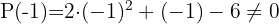
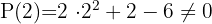
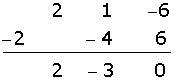
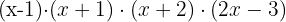
Colocamos o fator comum em evidência no último binômio e encontramos uma raiz racional.
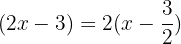
A fatoração do polinômio ficará:
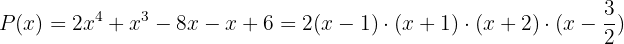
Raízes racionais
Pode acontecer que o polinômio não tenha raízes inteiras e só tenha raízes racionais. Nesse caso, consideramos os divisores do termo independente divididos pelos divisores do termo de maior grau, e aplicamos o Teorema do Resto e a Regra de Ruffini.
Comprovamos através de:
.
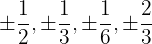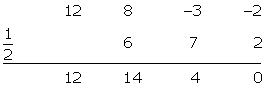
Fazemos a fatoração: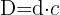 
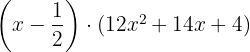
Voltamos a testar: 
Comprovamos por: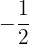 
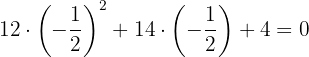
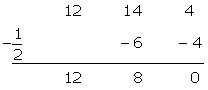
Fatoramos:
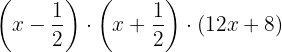
Colocamos o fator comum 
em evidência no terceiro fator.
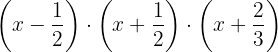
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
