Paolo Ruffini (1765–1822) foi um matemático italiano que desenvolveu um método mais prático para realizar a divisão de polinômios, quando o divisor é um binômio da forma x — a.
Regra de Ruffini
Para explicar os passos da aplicação da Regra de Ruffini, vamos considerar dois exemplos:
Primeiro exemplo da Regra de Ruffini
Divida 
1. Se o polinômio estiver completo, completamos os termos ausentes com coeficientes nulos:
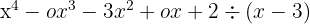
2. Escrevemos os coeficientes do dividendo em uma linha:
3. Abaixo à esquerda, colocamos o oposto do termo constante do divisor: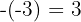
.
4. Traçamos uma linha e descemos o primeiro coeficiente 
.
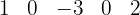
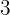
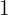
5. Multiplicamos esse coeficiente pelo número à esquerda 
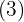e colocamos o resultado abaixo do próximo coeficiente 
.
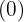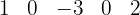
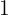
6. Somamos os coeficientes: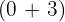 
.
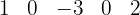
7. Repetimos o processo anterior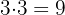 
et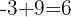 
).
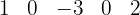
E repetimos novamente: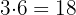 
et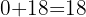 
(.
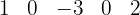
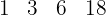
E mais uma vez: 
et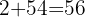 
.
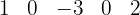
8. O último número obtido,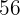 
, é o resto da divisão.
9. O quociente é um polinômio de grau uma unidade menor que o do dividendo, com coeficientes obtidos na última linha.
Quociente: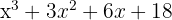 
Resto: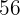
Segundo exemplo da Regra de Ruffini
Divida usando a regra de Ruffini: 
1. Quando o polinomio não está completo, completamos os termos ausentes com coeficientes nulos:
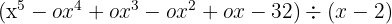
2. Escrevemos os coeficientes:
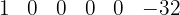
3. Abaixo à esquerda, colocamos o oposto do termo constante do divisor: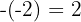 
.
4. Traçamos uma linha e baixamos o primeiro coeficiente: .
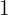
5. Multiplicamos esse coeficiente pelo divisor 
e somamos ao termo seguinte .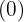
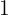
6. Somamos os dois coeficientes 
.
7. Repetimos os passos 
e 
até o final.
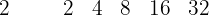
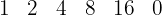
8. O quociente é um polinômio de grau inferior em uma unidade ao dividendo e cujos coeficientes são os que obtivemos.
Quociente: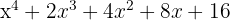 
Resto: 
Gostou desse artigo? Deixe uma nota!
Loading...
