Temas
Seja bem-vindo à seção de Exercícios de Polinômios para estudantes do Ensino Fundamental ao Ensino Médio!
Neste conjunto de exercícios, vamos explorar o universo dos polinômios, que são expressões algébricas formadas pela adição ou subtração de termos chamados monômios. Os polinômios são ferramentas fundamentais da álgebra e possuem diversas aplicações tanto na resolução de problemas matemáticos quanto na representação de fenômenos científicos.
Ao longo dos exercícios, vamos trabalhar com conceitos essenciais, como: identificação de termos semelhantes, soma e subtração de polinômios, multiplicação entre polinômios e, em alguns casos, também veremos fatoração e divisão de polinômios.
Esses exercícios foram desenvolvidos para reforçar seu entendimento sobre polinômios e ajudar a melhorar suas habilidades de manipulação algébrica.
Esperamos que você se sinta motivado e motivada a enfrentar os desafios propostos e encontre aqui a prática necessária para consolidar seus conhecimentos nesse tema tão importante e fascinante da matemática.
Vamos mergulhar nos exercícios e explorar as propriedades e operações desses objetos algébricos cheios de possibilidades!

Identificar monômios
Indique quais das seguintes expressões são monômios e, em caso afirmativo, indique grau e coeficiente.
1 
2 
3 
4 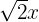
5 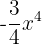
6 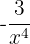
7 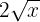
8 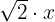
9 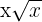
10 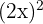
Indique quais das seguintes expressões são monômios e, em caso afirmativo, indique grau e coeficiente.
1 
Monômio, grau 3 e coeficiente
 .
.2 
Não é um monômio, pois o expoente não é um número natural.
3 
Não é um monômio, pois é uma soma de dois termos (polinômio).
4 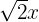
Monômio, grau 1 e coeficiente 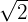 .
.
5 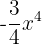
Monômio, grau 4 e coeficiente 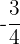 .
.
6 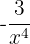
Não é um monômio, pois há variável no denominador (expoente negativo).
7 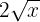
Não é um monômio, porque a variável está dentro de uma raiz (expoente fracionário).
8 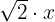
Monômio, grau 1 e coeficiente 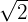 .
.
9 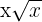
Não é um monômio, pois 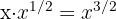 e o expoente não é natural.
e o expoente não é natural.
10 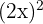
Monômio, grau 2 e coeficiente 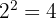 .
.
Operações com monômios
Faça as seguintes operações com monômios:
1 
2 
3 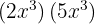
4 
5 
6 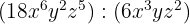
7 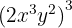
8 
9 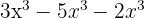
10 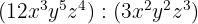
11 
12 
13 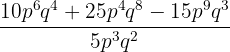
14 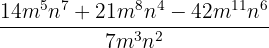
15 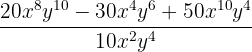
Faça as seguintes operações com monômios:
1 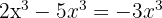
2 
3 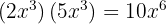
4 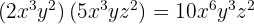
5 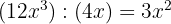
6 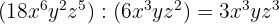
7 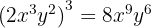
8 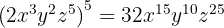
9 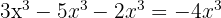
10 
11 
12
13 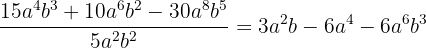
14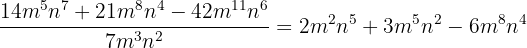
15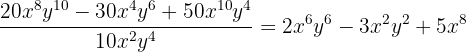
Identificar polinômios
Determine se as seguintes expressões algébricas são polinômios ou não. Em caso afirmativo, indique o grau e o termo independente.
1 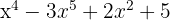
2 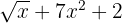
3 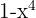
4 
5 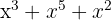
6 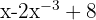
7 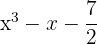
8 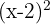
9 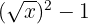
10 
Determine se as seguintes expressões algébricas são polinômios ou não. Em caso afirmativo, indique o grau e o termo independente.
1 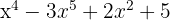
Polinômio, grau 5 e termo independente  .
.
2 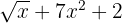
Não é um polinômio, pois a parte literal do primeiro termo está dentro de uma raiz.
3 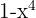
É um polinômio; grau 4 e termo independente  .
.
4 
Polinômio, pois o expoente do primeiro termo não é um número natural.
5 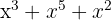
Polinômio; grau 5 e termo independente  .
.
6 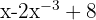
Não é um polinômio, pois o expoente do segundo termo não é um número natural.
7 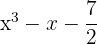
Polinômio; grau 3 e termo independente 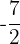 .
.
8 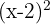
Polinômio; grau 2 e termo independente  .
.
9 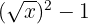
Polinômio; grau 1 e termo independente  .
.
10 
Não é um polinômio, pois o expoente não é um número natural.
Escreva em linguagem matemática
Escreva:
1Um polinômio ordenado sem termo independente.
2Um polinômio não ordenado e completo.
3Um polinômio completo sem termo independente.
4Um polinômio de grau 4, completo e com coeficientes ímpares.
5Um polinômio de grau 2, completo e com coeficientes negativos.
Escreva:
1Um polinômio ordenado sem termo independente.
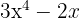
2Um polinômio não ordenado e completo.
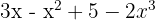
3Um polinômio completo sem termo independente.
Impossível
4Um polinômio de grau 4, completo e com coeficientes ímpares.
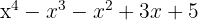
5Um polinômio de grau 2, completo e com coeficientes negativos.
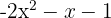
Cálculo com polinômios
Considerando os polinômios:
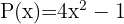



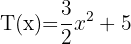

Calcule:
1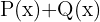
2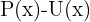
3
4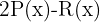
5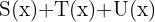
6
7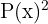
8
9
10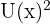
Considerando os polinômios:
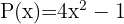



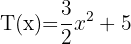

Calcule:
1 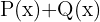
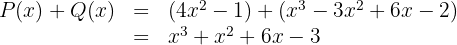
2 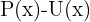
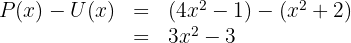
3 
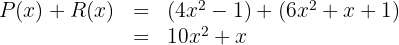
4 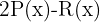
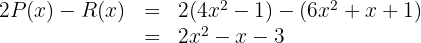
5 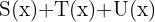
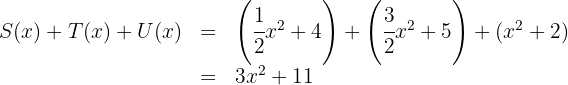
6 
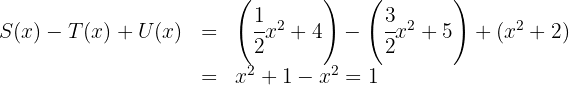
7 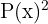
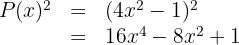
8 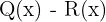
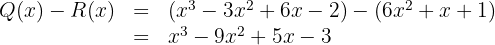
9 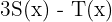
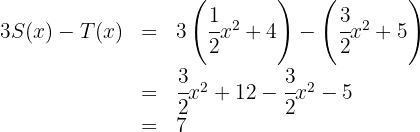
10 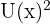
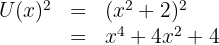
Multiplicações
Multiplique:
1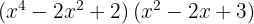
2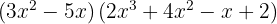
3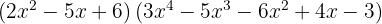
4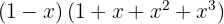
5
Multiplique:
1 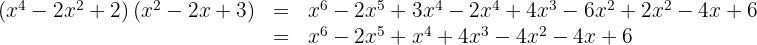
2 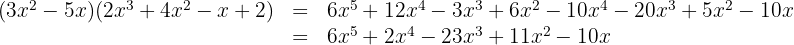
3 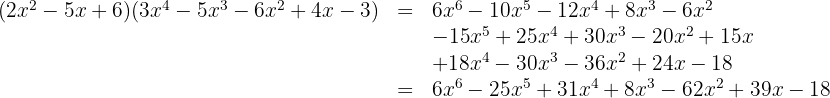
4 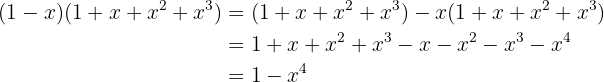
5 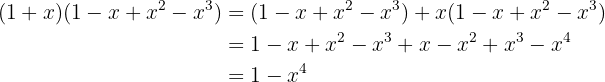
Encontrar o valor numérico do polinômio
Encontre o valor numérico do polinômio  , para:
, para: 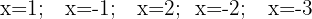 .
.
Encontre o valor numérico do polinômio  , para:
, para: 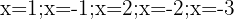 .
.
1 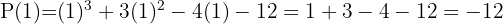
2 
3 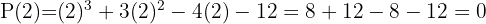
4 
5 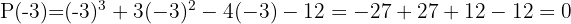
Cálculo
Calcule:
1
2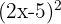
3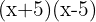
4
5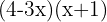
Calcule:
1 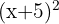
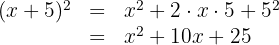
2 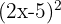
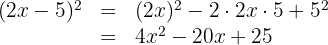
3 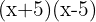
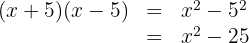
4 
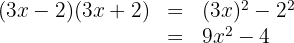
5 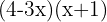
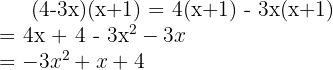
Divisão de polinômios
Divida:
1 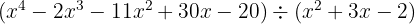
Quociente:  ; Resíduo:
; Resíduo: 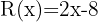
2 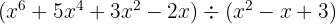
Quociente:  ; Resíduo:
; Resíduo: 
3 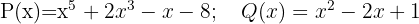
Quociente: 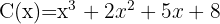 ; Resíduo:
; Resíduo: 
4 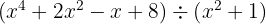
Quociente: 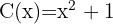 ; Resíduo:
; Resíduo: 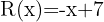
5 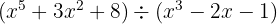
Quociente: 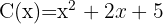 ; Resíduo:
; Resíduo: 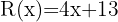
1 Quociente:  ; Resíduo:
; Resíduo: 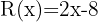
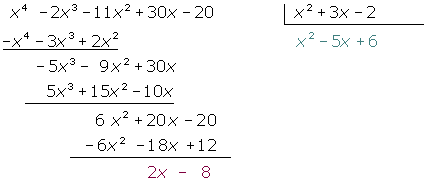
2 Quociente:  ; Resíduo:
; Resíduo: 
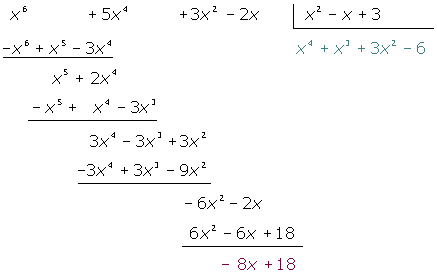
3 Quociente: 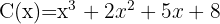 ; Resíduo:
; Resíduo: 
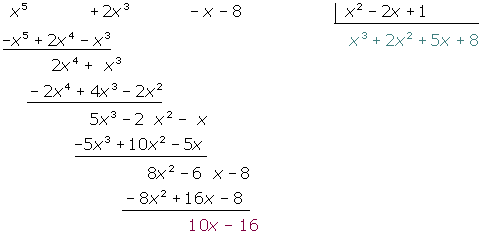
4 Quociente: 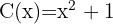 ; Resíduo:
; Resíduo: 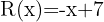
5 Quociente: 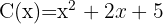 ; Resíduo:
; Resíduo: 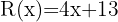
Regra de Ruffini
Faça a divisão usando o dispositivo prático de Briot-Ruffini, também conhecido como a Regra de Ruffini:
1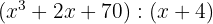
2
3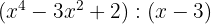
4
5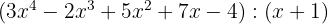
Faça a divisão usando o dispositivo prático de Briot-Ruffini, também conhecido como a Regra de Ruffini:
1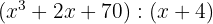
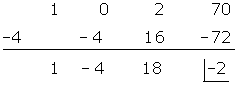
Quociente  ; Resíduo
; Resíduo 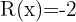
2
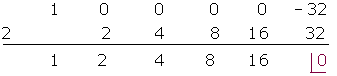
Quociente 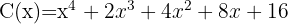 ; Residuo
; Residuo 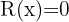
3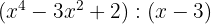
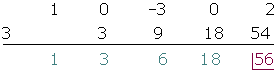
Quociente 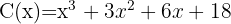 ; Resíduo
; Resíduo 
4
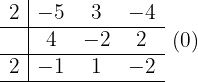

Resíduo: -2. 5
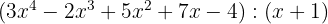

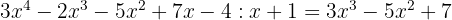
Resíduo: -2.
5 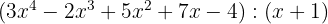

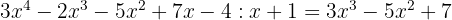
Resíduo: -11.
Resumir com IA:












