Temas
Calcule as derivadas das funções
a) 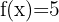
Neste caso, utilizamos a fórmula 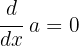 , que significa que a derivada de qualquer constante sempre é zero.
, que significa que a derivada de qualquer constante sempre é zero.

b) 
Neste caso, utilizamos a fórmula  , que significa que quando tenhamos uma constante multiplicando uma variável, a derivada será a constante.
, que significa que quando tenhamos uma constante multiplicando uma variável, a derivada será a constante.

c) 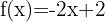
Neste caso, utilizamos a regra 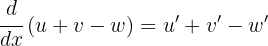 , que significa que quando tenhamos uma soma ou diferença de funções (ou termos algébricos), a derivada será equivalente à soma e/ou diferença das derivadas de cada função (ou termos algébricos).
, que significa que quando tenhamos uma soma ou diferença de funções (ou termos algébricos), a derivada será equivalente à soma e/ou diferença das derivadas de cada função (ou termos algébricos).

d) 
Neste caso, derivamos cada termo algébrico. Para o primeiro usamos a fórmula 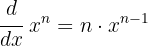 .
.

e) 
Neste caso, derivamos cada termo algébrico:
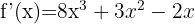
f) 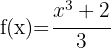
Neste caso, podemos reescrever a função como:
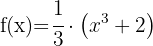
Assim, a derivada será  multiplicado pela derivada da função
multiplicado pela derivada da função 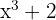
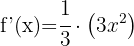

g) 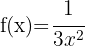
Para este tipo de função, das quais a variável encontra-se no denominador, podemos aplicar a propriedade das potências:
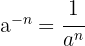
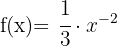
Para derivar, podemos aplicar a fórmula 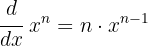
Assim, temos:
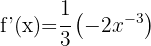

h) 
Para derivar um quociente usamos a fórmula:

Assim, a derivada é:
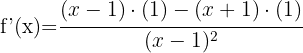

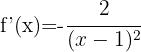
i) 
Para derivar um produto, aplicamos a fórmula:

Assim, a derivada é:
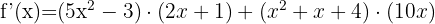
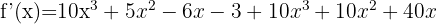
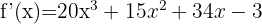
Calcule usando a fórmula da derivada de uma potência
Calcule usando a fórmula da derivada de uma potência
Lembre-se de que a fórmula para derivar uma potência é:
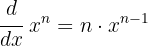
Utilizaremos esta fórmula em todos os exercícios desta seção
a) 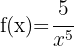
Utilizando as propriedades das potências, podemos reescrever a função desta maneira:

Aplicando a fórmula para derivar uma potência:
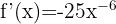
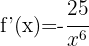
b) 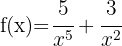
Utilizando as propriedades das potências, podemos reescrever a função desta maneira:

Aplicando a fórmula para derivar uma potência:
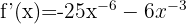

c) 
Utilizando as propriedades das potências, podemos reescrever a função desta maneira:
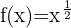
Aplicando a fórmula para derivar uma potência:


d) 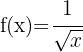
Utilizando as propriedades das potências, podemos reescrever a função desta maneira:

Aplicando a fórmula para derivar uma potência:
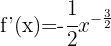
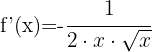
e) 
Utilizando as propriedades das potências, podemos reescrever a função desta maneira:
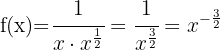
Aplicando a fórmula para derivar uma potência:
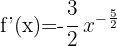
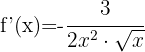
f) 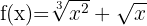
Utilizando as propriedades das potências, podemos reescrever a função desta maneira:
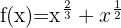
Aplicando a fórmula para derivar uma potência:
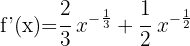
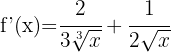
g) 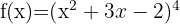
Neste caso, temos uma função elevada a uma potência, assim podemos usar a fórmula:
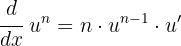

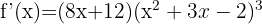
Calcule usando a fórmula da derivada de uma raiz
Calcule usando a fórmula da derivada de uma raiz
Para derivar funções que contém raízes, podemos convertê-las em potência (como na seção anterior), ou ainda, utilizar as seguintes fórmulas para derivar raízes:
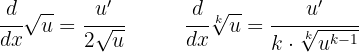
a) 
Por ser raiz quadrada, podemos utilizar a primeira fórmula
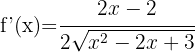
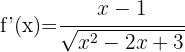
b) 
Por ser raiz quarta, utilizamos a segunda fórmula

c) 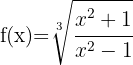
Por ser uma raiz cúbica, começamos a derivar usando a segunda fórmula. A função dentro da raiz é derivada com a fórmula do quociente 
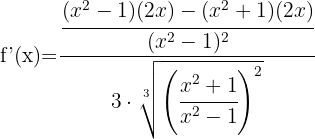
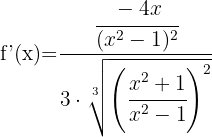
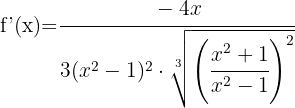
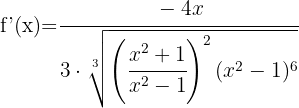
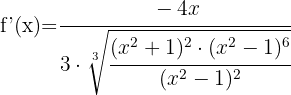
Simplificamos a expressão 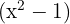 entre o numerador e o denominador, desfazendo-se deste último. Assim, obtemos:
entre o numerador e o denominador, desfazendo-se deste último. Assim, obtemos:
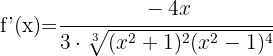

Calcule a derivada das funções exponenciais
Calcule a derivada das funções exponenciais
Nesta seção, as fórmulas que vamos usar são as seguintes:

a) 
Usamos a primeira fórmula. Assim, obtemos:
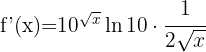
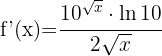
b) 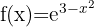
Usamos a segunda fórmula. Assim, obtemos:


c) 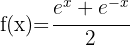
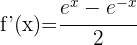
d) 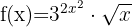
Começamos usando a fórmula do produto 

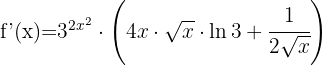
e) 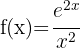
Começamos usando a fórmula do quociente 
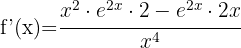
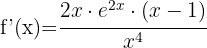

Calcule a derivada das funções logarítmicas
Calcule a derivada das funções logarítmicas
Nesta seção, usaremos as seguintes fórmulas:
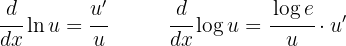
Além disso, podemos usar as propriedades dos logaritmos para reescrever a função de uma forma mais simples para derivar
a) 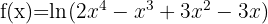
Usamos a fórmula para derivar logaritmos neperianos
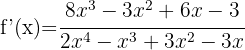
b) 
Usando a propriedade dos logaritmos, 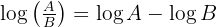 obtemos:
obtemos:

Derivamos cada termo aplicando a fórmula para derivar logaritmos neperianos
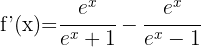
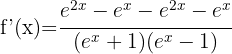
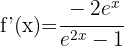
c) 
Usamos as propriedades dos logaritmos 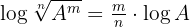 e
e 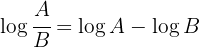 obtemos
obtemos

Usando a fórmula para derivar logaritmo, obtemos


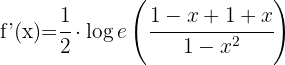
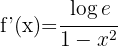
d) 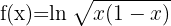
Usando as propriedades dos logaritmos 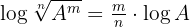 e
e 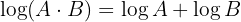 obtemos
obtemos
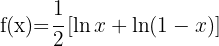
Usando a fórmula para derivar logaritmos neperianos, obtemos
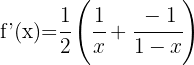
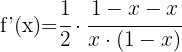
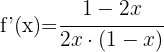
e) 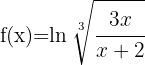
Usando as propriedades dos logaritmos 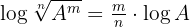 e
e 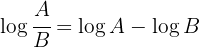 obtemos
obtemos

Usando a fórmula para derivar logaritmos neperianos, obtemos

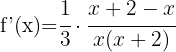

Resumir com IA: