Inclinação da reta tangente
A inclinação da reta tangente a uma curva em um ponto é igual à derivada da função nesse ponto.
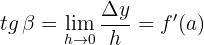
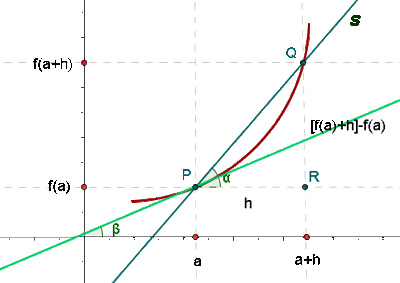
Exemplo: Determine a inclinação da reta à curva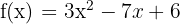 
para 
1Calculamos a derivada
2 A inclinação que estamos buscando é:
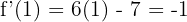
Equação da reta tangente
A reta tangente a uma curva em um dado ponto é a reta que passa pelo ponto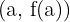 
e cuja inclinação é igual a 
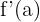. Sua equação é dada por:
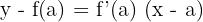
Exemplo: Encontre a reta tangente à curva 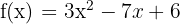em
1 Calculamos o ponto do gráfico da curva por onde passa a reta tangente:
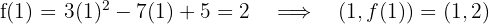
2 Calculamos a inclinação da reta tangente em 
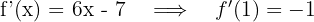
3 A equação da reta tangente é
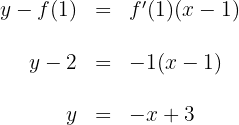
Exercícios propostos
Determine os pontos da curva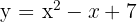 
onde a reta tangente é paralela ao eixo 
1 Calculamos a derivada da curva:
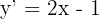
2 O eixo tem inclinação zero. A inclinação da reta tangente é igual à derivada e retas paralelas têm a mesma inclinação.
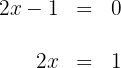
portanto, valor de 
é: 
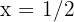
3 Calculamos o valor 
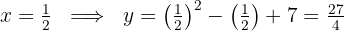
O ponto que buscamos é: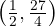 
Calcule os pontos a tangente da curva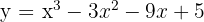 
fica paralela ao eixo .
1 Calculamos a derivada da curva
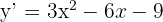
2 O eixo tem inclinação zero, a inclinação da reta tangente é igual à derivada e retas paralelas têm a mesma inclinação.
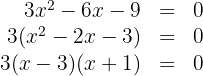
portanto, os valores de são 
e 
3 Calculamos os valores
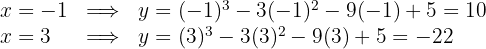
Os pontos buscados são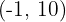 
e 
Foi traçada uma reta tangente à curva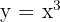 
, que tem como inclinação 
e passa pelo ponto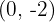 
. Encontre o ponto de tangência.
1 Calculamos a derivada da curva
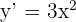
2 Como a inclinação é , igualamos à derivada e encontramos os valores dos pontos de tangência com inclinação três
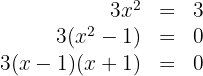
portanto os valores de são e
3 Calculamos os valores de
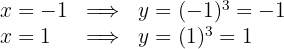
Os pontos buscados são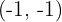 
e 
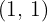
4 A equação da reta tangente com ponto de tangência 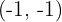é
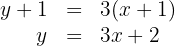
que não passa pelo ponto .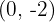
A equação da reta tangente com ponto de tangência 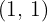é:
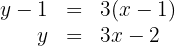
que passa pelo ponto .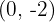
Assim, o ponto de tangência solicitado é .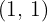
Encontre a reta tangente à curva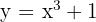 
em 
.
1 Calculamos a derivada da curva
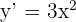
2 Como a inclinação é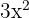 
, substituímos 
e encontramos o valor da inclinação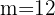 
3 Calculamos o valor de onde passa a reta tangente
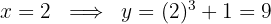
O ponto procurado é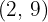 
4 A equação da reta tangente com ponto de tangência 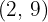é:
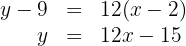
Encontre os pontos da curva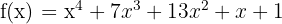 
, em que a tangente forma um ângulo de 
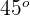com o eixo .
1 Calculamos a derivada da curva:
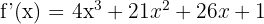
2 A inclinação é igual a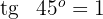 
. Igualamos esta inclinação com a derivada e encontramos os valores dos pontos de tangência com inclinação três:
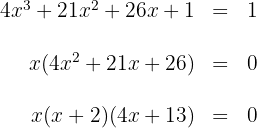
portanto os valores de são 
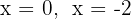e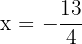 
3 Calculamos os valores da segunda coordenada dos pontos de tangência
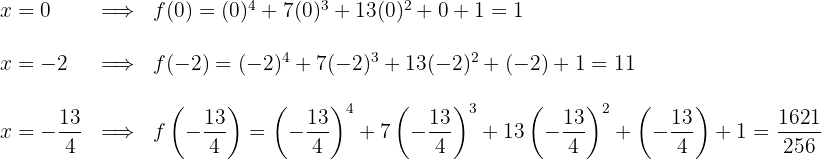
Os pontos procurados são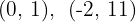 
e 
Considerando a função 
, ache o ângulo que forma a reta tangente do gráfica da função 
na origem, com o eixo de abscissas.
1 Calculamos a derivada da curva
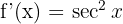
2 A inclinação na origem é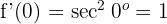 
. Portanto, o ângulo formado entre a reta tangente e o eixo das abscissas é:
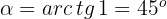
Considerando a função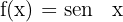 
, encontre o ângulo que forma a reta tangente do gráfico da função na origem com o eixo de abscissas.
1 Calculamos a derivada da função
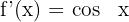
2 A inclinação no ponto de origem é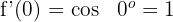 
. Portanto, o ângulo formado entre a reta tangente e o eixo das abscissas é:
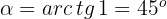
Determine os coeficientes da equação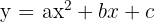 
, sabendo que seu gráfico passa 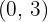por 
e por 
, e no último ponto, sua tangente tem inclinação .
1 Calculamos a derivada da curva
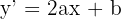
2 Substituindo os dois pontos por onde passa o gráfico na equação dada e a inclinação da reta tangente, obtemos o seguinte sistema de três equações:
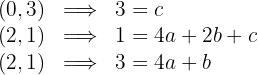
3 O sistema de equações
tem como solução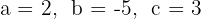 
Determine os coeficientes da equação 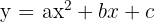, sabendo que seu gráfico passa por 
e por 
, sendo a reta tangente à curva no ponto de abcissa 
paralela à bissetriz do primeiro quadrante. Encontre o valor numérico dos coeficientes da equação.
1 Calculamos a derivada da curva
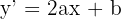
2 Substituindo os dois pontos por onde passa o gráfico na equação dada e a inclinação da reta tangente que é , obtemos o seguinte sistema de três equações
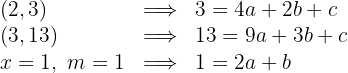
3 O sistema de equações
tem como solução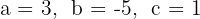 
Determine os coeficientes da equação 
, sabendo que seu gráfico passa 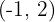por 
e por , sendo a reta tangente à curva nos pontos de abcissas e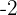 
paralela ao eixo das abcissas. Encontre o valor numérico dos coeficientes da equação.
1 Calculamos a derivada da curva
2 Substituindo os dois pontos por onde passa o gráfico na equação dada e a inclinação da reta tangente que é 
, obtemos o seguinte sistema de quatro equações
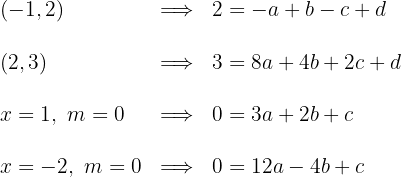
3 O sistema de equações
tem como solução 
Gostou desse artigo? Deixe uma nota!
Loading...
