Temas

O que é a Regra de Cramer?
Em Álgebra Linear, a Regra de Cramer é uma fórmula explícita usada para resolver um sistema de equações lineares que possui o mesmo número de equações e incógnitas. A Regra de Cramer só é válida quando o sistema possui solução única.
Observação: Esse sistema recebeu esse nome em homenagem a Gabriel Cramer (1704–1752), que publicou a regra para um número arbitrário de incógnitas em 1750.
A Regra de Cramer é aplicada para resolver sistemas de equações lineares que atendem às seguintes condições:
1 O número de equações é igual ao número de incógnitas.
2 O determinante da matriz dos coeficientes é diferente de zero.
Sistemas que satisfazem essas condições são sistemas compatíveis determinados e são chamados de sistemas de Cramer.
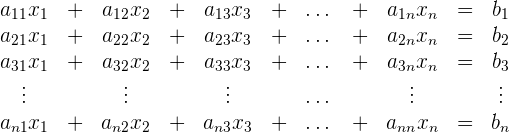
Considere Δ o determinante da matriz de coeficientes:

Vamos relembrar que o cálculo do determinante é dado por:
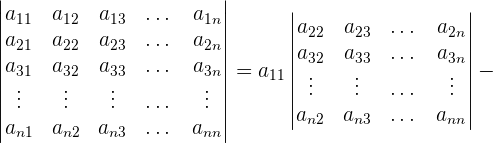
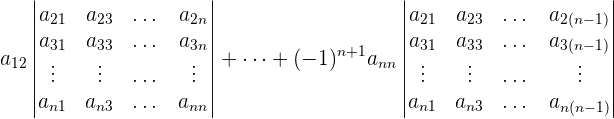
Nos casos de 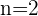 e
e 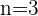 , é possível calcular obter os resultados através de cálculos simples:
, é possível calcular obter os resultados através de cálculos simples:
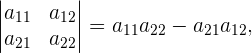
e
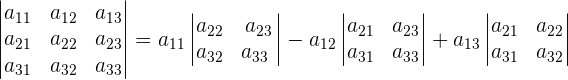
Fórmula para resolver sistemas de Cramer
Todo sistema de Cramer possui uma única solução (ou seja, é um sistema compatível determinado) e essa solução é dada pelas expressões:
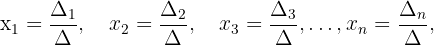
onde 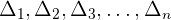 são os determinantes obtidos ao substituir os coeficientes do 2º membro (os termos independentes) na 1ª coluna, na 2ª coluna, na 3ª coluna e na enésima coluna, respectivamente.
são os determinantes obtidos ao substituir os coeficientes do 2º membro (os termos independentes) na 1ª coluna, na 2ª coluna, na 3ª coluna e na enésima coluna, respectivamente.





Exemplos de exercícios resolvidos pela regra de Cramer
1
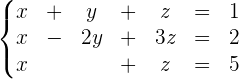
Observamos que o número de equações deste sistema é igual ao número de incógnitas e, além disso,
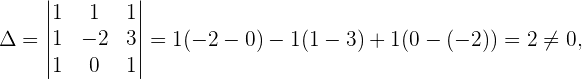
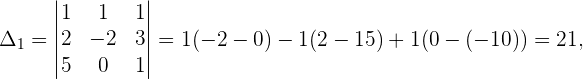
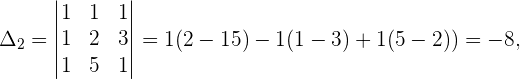
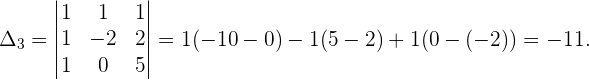
Como 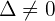 , temos que o sistema é um sistema de Cramer e possui como soluções:
, temos que o sistema é um sistema de Cramer e possui como soluções:
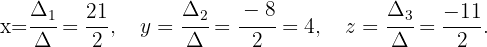
2
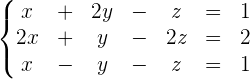
Este sistema tem o mesmo número de equações e de incógnitas, mas o determinante de sua matriz de coeficientes é zero, pois,
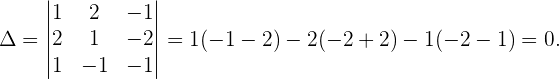
Assim, trata-se de um sistema compatível indeterminado.
Como o sistema não é um sistema de Cramer, precisamos transformá-lo em um.
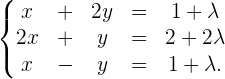
Considerando que a equação 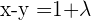 é uma combinação linear das equações
é uma combinação linear das equações 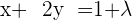 e
e 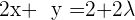 ,
,
então, podemos trabalhar com o sistema:
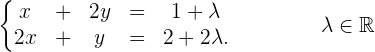
Estamos diante de um sistema com o mesmo número de equações que de incógnitas e com determinante da matriz de coeficientes diferente de zero,
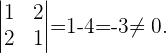
Ou seja, estamos diante de um sistema de Cramer.
As soluções desse sistema de Cramer, que serão expressas em função de λ,, serão as mesmas soluções do sistema original.

E, por fim, substituímos esses valores nas fórmulas já conhecidas.
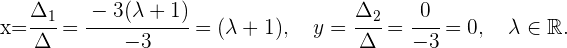
Resumir com IA:












