A derivação pela regra da cadeia é aplicada quando buscamos derivar uma composição de funções.
Se temos uma função composta da forma
então sua derivada, em relação a 
, é dada por:
ou, na notação com diferenciais,
Devemos observar cuidadosamente que 
é a derivada de 
, mas em termos de 
.
A demonstração pela definição é a seguinte:
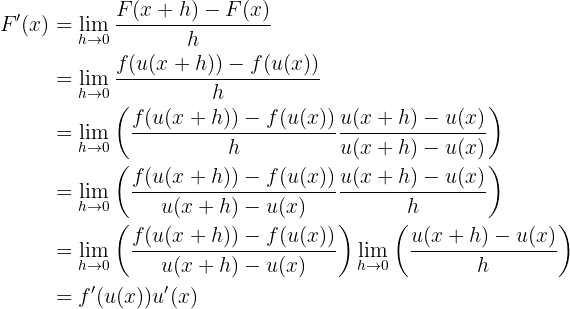
Agora veremos alguns exercícios em que aplicaremos a regra da cadeia.
Derive a seguinte função:
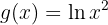
Observamos que, neste caso, é conveniente definir: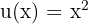
e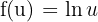 
.
Dessa forma, temos;
e, por sua vez,
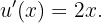
Assim, aplicando a regra da cadeia, a derivada é dada por:
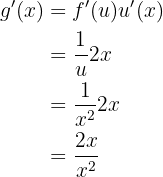
Derive a seguinte função:
Observamos que, neste caso, é conveniente definir:
e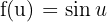 
.
Dessa forma, temos;
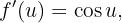
enquanto que,
Assim, aplicando a regra da cadeia, a derivada é dada por:
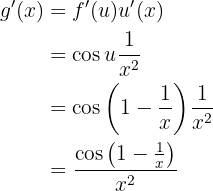
Derive a seguinte função:
Observamos que, neste caso, há uma composição dupla; portanto, aplicaremos a regra da cadeia duas vezes. Inicialmente, consideramos
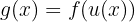
em que 
e 
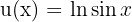. Assim, temos
Agora, derivamos 
. Observe que essa função também pode ser escrita como uma composição, isto é,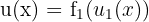
, em que 
e 
.
Suas derivadas são
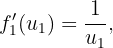
e
Portanto, a derivada procurada é dada por
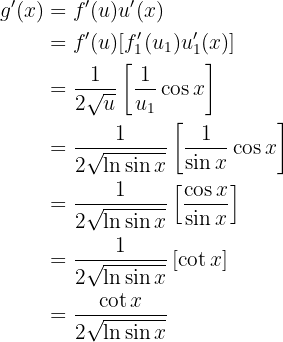
Derive a seguinte função:
Neste caso, podemos definir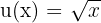
e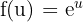 
.
Assim, temos
e, por outro lado,
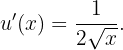
Portanto, aplicando a regra da cadeia, obtemos
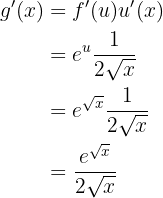
Derive a seguinte função:
Neste caso, podemos definir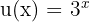
e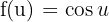 
.
Dessa forma, temos
e, além disso,
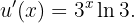
Assim, aplicando a regra da cadeia, obtemos
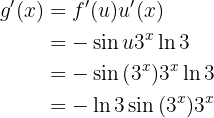
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
