
O que são funções implícitas?
As funções implícitas são aquelas que aparecem em termos de “x” e “y”, e nenhuma das variáveis está isolada. Para calcular a derivada de forma implícita, não é necessário isolar o “y”, em muitos casos, isso nem sequer é possível. Basta derivar membro a membro, aplicando as regras de derivação e lembrando que:
- x'=1
- Em geral y'≠1
- Por isso, omitimos o x′ e mantemos o y′
- Quando as funções são mais complexas, utilizamos uma regra para facilitar o cálculo:
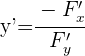
Exercícios de funções implícitas
Derive as seguintes funções implícitas

Derivar 
1 Derivamos cada termo separadamente: o que contém “y”, em relação a “y”, e o que contém “x”, em relação a “x”.

2 Isolamos y'




Derivar 
1 Derivamos cada termo separadamente. O termo que contém “y”, derivamos em relação a “y”; o que contém “x”, em relação a “x”. Os termos que contêm ambas as variáveis são derivados duas vezes, uma em relação a “x” e outra em relação a “y”.
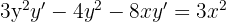
2 Devemos isolar y′. Para isso, deixamos de um lado os termos que o contêm e passamos os demais para o outro lado.
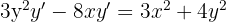
3 Fatoramos e isolamos y′


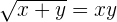
Derivar 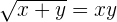
1 Derivamos cada termo separadamente. Neste caso, derivamos ambos os membros: uma vez em relação a “x” e outra em relação a “y”.
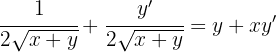
2 Devemos isolar y', para isso podemos deixar de um lado os termos que contenham y' e os que não o contenham passamos para o outro lado e resolvemos as operações com frações.
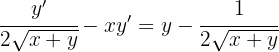
3 Resolvemos as frações, colocamos y′ em evidência e isolamos.
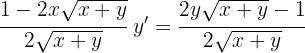

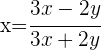
Derivar 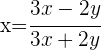
1 Derivamos cada termo separadamente, aqueles que contêm ‘x’ e ‘y’ são derivados duas vezes, uma para cada variável. No segundo membro da igualdade devemos usar a fórmula para derivar um quociente.

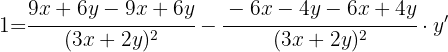

2 Devemos isolar y', para isso podemos deixar de um lado os termos que contenham y' e os que não o contenham passamos para o outro lado e resolvemos as operações com frações.



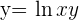
Derivar 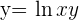
1 Derivamos cada termo separadamente. O que contém ‘y’ em relação a ‘y’ e o que contém ‘x’ em relação a ‘x’. Os termos que contêm ambas as variáveis são derivados 2 vezes, uma em relação a ‘x’ e outra em relação a ‘y’.
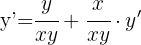
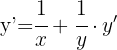
2 Devemos isolar y', para isso podemos deixar de um lado os termos que contenham y' e os que não o contenham passamos para o outro lado.
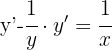
3 Fatoramos por fator comum e isolamos y'.
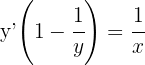
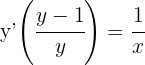

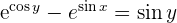
Derivar 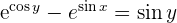
1 Por ter várias funções transcendentes passaremos todos os termos a um membro da igualdade e aplicaremos: 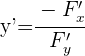
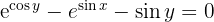
2 Calculamos  e
e 
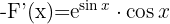
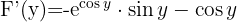
3 Substituímos em 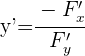

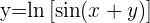
Derivar 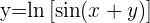
1 Por ter várias funções transcendentes passaremos todos os termos a um membro da igualdade e aplicaremos: 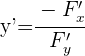

2 Calculamos  e
e 
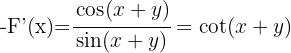
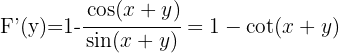
3 Substituímos en 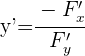


Derivar 
1 Calculamos  e
e 
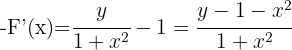
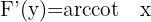
2 Substituímos en 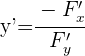


Derivar 
1 Multiplicamos ambos os membros por  para eliminar a fração e passamos todos os termos a um só membro da igualdade.
para eliminar a fração e passamos todos os termos a um só membro da igualdade.
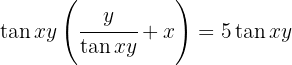

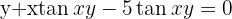
2 Calculamos  e
e 
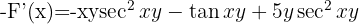

3 Substituímos en 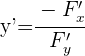
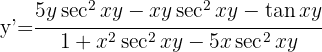

Derivar 
1 Por ter várias funções transcendentes passaremos todos os termos a um membro da igualdade e aplicaremos: 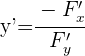
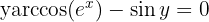
2 Calculamos  e
e 


3 Substituimos en 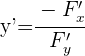

Resumir com IA:












