Temas
A inclinação da reta tangente a uma curva em um ponto
Em uma reta tangente a uma curva em um ponto, sua inclinação é a derivada da função nesse ponto e se expressa da seguinte maneira:
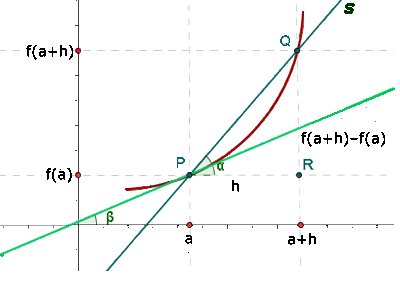
A reta tangente a uma curva em um ponto
Da mesma forma, a reta tangente a uma curva em um ponto é aquela que passa pelo ponto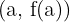 
e cuja inclinação é igual a 
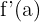, uma vez que se conhece a inclinação da reta e os pontos pelos quais ela passa, sua equação é:
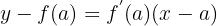
Exemplo da equação da reta tangente
Encontre a equação da reta tangente à parábola 
, que é paralela à reta 
.
Primeiro: Da equação da reta, isolamos 
da seguinte maneira:
Segundo: Com as informações descritas anteriormente, sabemos que a inclinação da reta é a derivada da função anterior, que corresponde ao coeficiente da mesma:
Terceiro: Com base no anterior, as duas retas paralelas devem ter a mesma inclinação, portanto, se derivamos a equação da parábola temos que:
Sendo a mesma inclinação para as duas retas:
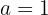
Quarto: Uma vez que se tem o valor da coordenada 
, substituímos esse valor na equação da parábola para encontrar a segunda coordenada da função:
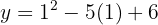
Quinto: Finalmente, aplicamos a equação da reta ponto-inclinação:
Observe que, como a reta é paralela à curva dada, elas têm a mesma inclinação.
Gostou desse artigo? Deixe uma nota!
Loading...
