A matemática não mente. Mente quem faz mau uso dela.
Albert Einstein
Os matemáticos e os números nos rodeiam permanentemente, um pouco como se vivêssemos na matriz de Neo (como no filme Matrix!). Quando você olha para sua casa, a posição das ruas de seu bairro, liga o seu carro ou liga a sua máquina de lavar roupa, faz uma gambiarra, pinta um quadro, toca piano, a matemática está exatamente em tudo!
Não há um objeto que não tenha sido feito com reflexões matemáticas. Equações complexas de vários desconhecidos, teoremas matemáticos que datam da antiguidade, até as últimas descobertas do século XX sempre fascinaram nosso mundo! A cada nova equação matemática, aparece uma inundação de questões e novas respostas sobre nosso mundo físico.
Em 2013, o autor Ian Stewart, matemático e cientista britânico de renome, publicou o livro intitulado As 17 equações que mudaram o mundo (Ed. Zahar). Fazer matemática é... como mudar o mundo! Se você quiser entender porque a matemática é tão importante, quais impactos cada equação matemática causaram no mundo, descubra agora as algumas fórmulas totalmente revolucionárias para seus curso de matematica basica ou avançada.

O Teorema de Pitágoras - uma equação matemática complexa
Uma equação é uma sentença matemática que possui incógnitas e uma igualdade. Toda equação matemática possui uma igualdade e pelo menos uma incógnita, e o objetivo é encontrar o valor da incógnita, que torne a igualdade verdadeira.
O Teorema de Pitágoras é com certeza uma das equações matemáticas mais conhecidas. Todo mundo estudou essa fórmula na escola em algum momento da vida.

Mesmo depois de anos sem praticar ou fazer um curso de matematica, o nome desse teorema deve estar aí, no fundo de sua memória. Todo mundo o conhece de cor, mas vamos lembrar dele rapidamente: em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos. Resumindo: a2 + b2 = c2
Esse teorema contribui até hoje com a história da matemática. Para entender melhor o teorema e sua importância, essa equação mudou nosso olhar da geometria plana. Eles dizem que a gente passou de uma geometria euclidiana para uma geometria não-euclidiana.
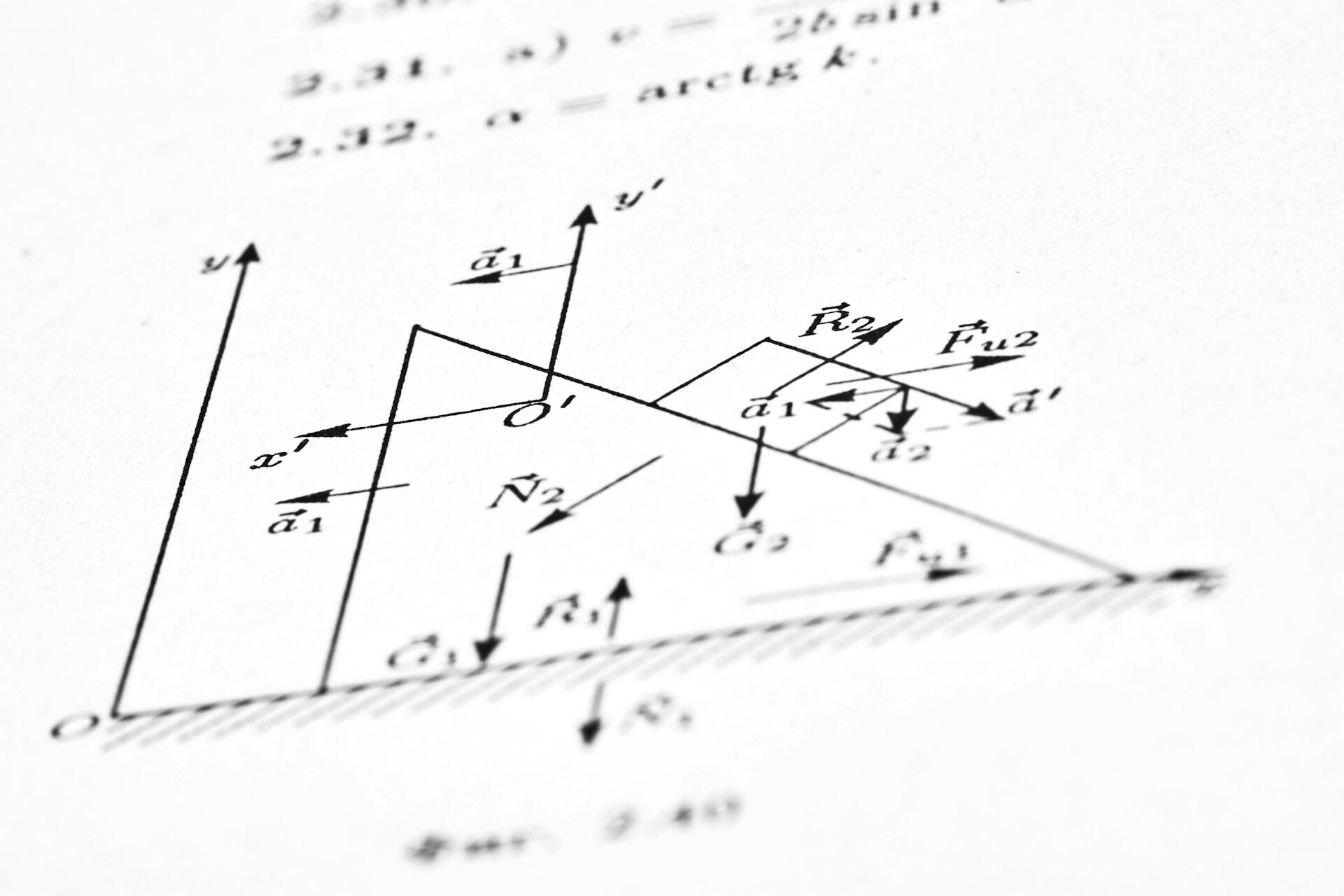
Graças a Pitágoras e sua famosa equação, hoje é possível e mais fácil de calcular o comprimento, os ângulos e demonstrar que tal triângulo é retângulo. A gente sempre encontra essa noção no universo da engenharia civil e na arquitetura.
Quer rever um pouco sobre a história da matemática e sua importância? Que tal um curso de matematica online?
O poder dos logaritmos nas equações matemáticas
Os logaritmos, popularizados por John Napier em 1610, são ferramentas essenciais para simplificar qualquer equação matemática complexa. Essencialmente, os logaritmos reagrupam as funções inversas, as opostas e das funções exponenciais. Isso permite que operações de divisão sejam transformadas em somas e subtrações, facilitando a resolução de expressões matemáticas de alto nível.
Até o desenvolvimento do computador, o cálculo com os logaritmos era a maneira mais comum de multiplicar grandes números. Essa grande inovação acelerou o tempo de cálculo e permitiu calcular mais rapidamente mas, principalmente, fazer saltos gigantes nas áreas de matemática, física, engenharia, navegação, cartografia e astronomia.
Existem 3 tipos de logaritmos:
- O logaritmo neperiano ou natural, que é a base fundamental na análise matemática. Utiliza a base e (número de Euler)
- O logaritmo decimal é utilizado em cálculos de matemática. Utiliza a base 10. É mais frequente em equações matemáticas escolares e em escalas de medida.
- O logaritmo binário é utilizado na teoria da informática e para os cálculos aplicados (em curso de matemática, ciência da computação e teoria da informática). Utiliza a base 2.
logb(x) = y ↔️by = x
O logaritmo é o expoente (ou potência) a que outro valor fixo, a base, deve ser elevada para produzir este número. A potência de 3 do número 2 é 8 (8 = 2 × 2 × 2 = 23).
Ao lidar com a base 10, a lógica de uma equação matemática complexa segue este padrão:
- log(1) = 0
- log(10) = 1
- log(100) = 2
Além das ciências exatas, o domínio dessas equações complexas possui aplicações práticas curiosas. A gente pode, por exemplo, se servir da matemática para o pôker e para solucionar enigmas de criptografia.
Lei da Gravidade: como uma maçã virou uma equação matemática complexa?
Quem nunca ouviu falar da lei da gravidade de Isaac Newton? A famosa história da maçã que caiu na cabeça do gênio em 1687, enquanto ele admirava a lua no céu? Esse acontecimento é o ponto de partida para uma das mais fundamentais equações matemáticas da história.
Foi fazendo a aproximação desses dois corpos (a lua e a maçã) que Newton se pergunta: por que a lua não cai da mesma forma que a maçã?
A resposta reside na força de atração universal! Ou seja, a lua não cai porque ela é retida por uma força gravitacional. Naquele exato momento ele compreendeu que os dois corpos estavam sob influência da mesma força, mas em condições de velocidade e de distância diferentes.

Foi assim que nasceu a célebre fórmula da lei da gravidade ou Lei da Gravitação Universal de Newton: "os astros se atraem proporcionalmente ao produto de suas massas e é inversamente proporcional ao quadrado da distância que os separam".
Para provar a teoria que acabava de descobrir, Newton desenvolveu equações complexas que descrevem como a matéria se comporta no universo. Matematicamente, essa equação matemática complexa é expressa como:
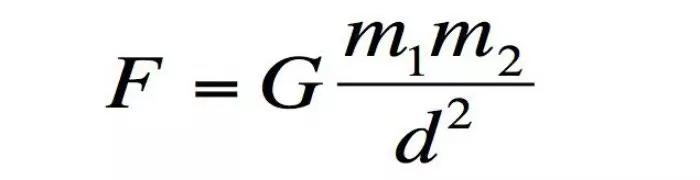
Onde:
- F é a força gravitacional entre os dois objetos;
- G é a constante gravitacional universal
- m1 e m2 são as massas dos objetos;
- r é a distância entre os centros das massas.
Cerca de 200 anos depois de Newton, a compreensão sobre essas equações matemáticas deu um salto ainda maior. Albert Einstein troca a Teoria da Gravidade para a Teoria da Relatividade, refinando os cálculos.
A Teoria da Relatividade
Mesmo se você não tem muita afinidade com as ciências exatas como a física e a matemática, certamente já deve ter se deparado em algum momento da sua vida com a expressão E = mc²de Albert Einstein. Esta é sem dúvida a equação matemática mais famosa de Einstein. Mas o que ela realmente representa para o mundo da física?
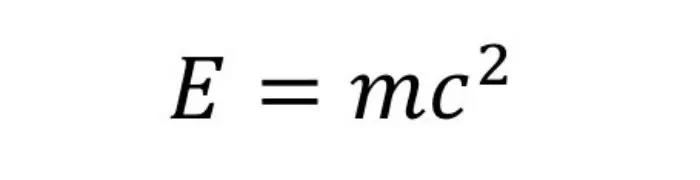
Essa equação matemática ilustra a teoria da relatividade (relatividade restrita e relatividade geral) mudou completamente os códigos da física conhecidos até então ao demonstrar que:
- A matemática pode ser convertida em energia;
- A energia pode ser convertida em matéria;
- A velocidade da luz é o limite absoluto de velocidade no universo.
Ela continua a revolucionar até hoje porque ela mostra que a matéria pode ser convertida em energia e vice-versa.

A relatividade restrita (1905) aborda a ideia que a velocidade da luz é uma constante universal que não vai se modificar e que a passagem de tempo não é a mesma para as pessoas que se deslocam em velocidades diferentes.
A relatividade geral (1915) de Einstein descreve que a matéria (energia) curva o espaço e o tempo à sua volta. Isto é, a gravitação é um efeito da geometria do espaço-tempo. Isso gerou uma revolução tão grande quanto a Lei da Gravidade de Newton.
Na relatividade geral, a gravitação não é apenas uma força como pensava Newton, mas sim um efeito da geometria do espaço-tempo. Simplificando: a matéria diz ao espaço como se curvar e o espaço diz à matéria como se mover.
Até hoje, as teorias da relatividade de Einstein são essenciais para entender a origem, a estrutura e o destino do nosso universo. A matemática permite de conhecer melhor o mundo. A gente pode facilmente perceber a onipresença da matemática no nosso cotidiano.
Dominar equações complexas nos permite:
- Compreender fenômenos astronômicos como os buracos negros e as ondas gravitacionais;
- Desenvolver tecnologias de ponta como o GPS por exemplo;
- Solucionar problemas lógicos do nosso cotidiano.
Porque não fazer mais aula de matematica se a matemática está em tudo?
Teoria do Caos: quando a ordem se torna uma equação matemática complexa
O que é muito interessante e torna a Teoria do Caos fascinante é que ela demonstra que a gente não pode prever com determinação aquilo que vai acontecer. Ou seja, nem tudo no universo pode ser previsto com precisão determinística.
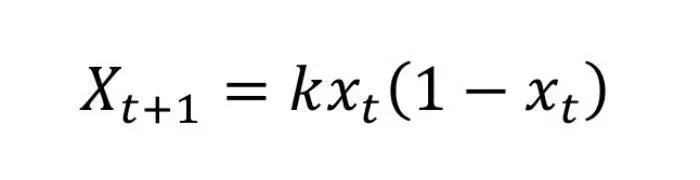
Embora a maioria das pessoas associem o caos a falta de regras, na verdade, ele estuda o comportamento de sistemas dinâmicos que seguem equações complexas onde pequenas variações iniciais mudam tudo.
A teoria de Robert May é muito recente porque ela data de 1975. Ela descreve um processo em constante evolução através do tempo. Em sua pesquisa, May utilizou uma equação matemática complexa para explicar como comportamento aparentemente aleatórios, como as flutuações populacionais ou a meteorologia, podem resultar em sistemas completamente diferentes em curtos intervalos de tempo.

Em sua fórmula, May queria explicar que um comportamento caótico (como a meteorologia que sofre cada vez mais mudanças climáticas) pode conduzir a um outro sistema completamente diferente de alguns dias atrás.
A ilustração mais conhecida é aquela chamada de "efeito borboleta" que diz que "o batimento das asas de uma borboleta no Brasil pode causar um furacão ou um tornado na Ásia". Matematicamente, isso significa que em certas equações matemáticas, uma mudança na milésima casa decimal de uma variável inicial pode levar a um resultado final astronômico.
Em outras palavras, as coisas mais insignificantes podem ter um impacto impensável em nossa volta ou bem longe.
Aliás, a gente pode mesmo associar a matemática com a sedução!
É a multiplicidade de fatores que transforma todo evento imprevisível. A Teoria do Caos nos mostra que o mundo é dinâmico e interconectado. Entender essas equações matemáticas nos ajuda a aceitar a incerteza e admirar ainda mais a complexidade do universo.

A Identidade de Euler: a equação matemática mais bela do mundo
Dentro do vasto universo das equações matemáticas, existe uma que se destaca muito pela sua elegância e simplicidade. A identidade de Euler é considerada "a mais bela das equações matemáticas complexas" dos cursos de matemática porque ela valoriza uma combinação improvável de 5 constantes matemáticas.
Por que essa equação é tão admirada? Porque ela utiliza 3 operações fundamentais da aritmética: adição, multiplicação e exponenciação.
eiπ + 1 = 0
As 5 constantes da Unificação: esta equação matemática complexa reúne elementos que parecem pertencer a ramos completamente distintos da ciência:
- O número 0: elemento neutro da adição e o ponto de partida da aritmética.
- O número 1: elemento neutro da multiplicação, base de todos os números inteiros.
- O número e: base dos logaritmos naturais, essencial em cálculos diferenciais e no estudo de crescimentos exponenciais.
- O número π: a constante que define a relação entre a circunferência e o diâmetro de um círculo.
- A unidade imaginária i: definida como a raiz quadrada de -1, ela é a base dos números complexos, fundamentais para resolver equações complexas na engenharia elétrica e na física quântica.
Essa equação, que decora o Palácio da Descoberta em Paris, abriu o caminho para o desenvolvimento da topologia, um ramo da matemática moderna que estuda as propriedades das figuras geométricas. Essa bela equação mostra que mesmo as equações complexas podem ser resumidas com extrema simplicidade.
Transformada de Fourier: o prisma das equações matemáticas
A transformada de Fourier recorta o tempo em várias frequências e ondas simples como um prisma desconstrói a luz em vários raios coloridos. É a base de quase toda tecnologia digital que usamos hoje.

Um outro exemplo poderia ser um campo magnético ou um campo acústico que a gente define como um sinal, a transformada de Fourier é seu espectro: ela desconstrói o campo acústico ou magnético.
Originalmente desenvolvida por Joseph Fourier em 1822, essa teoria foi uma extensão para as funções não periódicas. Em termos práticos, ela pega uma equação matemática complexa que representa um ruído confuso e desconstrói em uma soma de ondas senoidais puras.

A famosa capa do disco "Dark Side of The Moon" do Pink Floyd é uma metáfora visual perfeita para o que Fourier faz com a matemática: separar o complexo em seus componentes fundamentais e coloridos.
Essa teoria mudou completamente nosso mundo porque, de repente, era possível entender a estrutura das ondas mais complexas como a da fala humana. Hoje, a gente revê essa teoria que data de 1822 no centro do tratamento moderno de sinais, reconhecimento de voz, análises e tratamentos de dados.
As equações de Maxwell
As equações de Maxwell descrevem como interagem as cargas elétricas mas também as correntes de energia e os campos magnéticos. Também conhecidas como equações de Maxwell-Lorentz, elas formam o conjunto de leis fundamentais que regem o comportamento da luz e das ondas de rádio
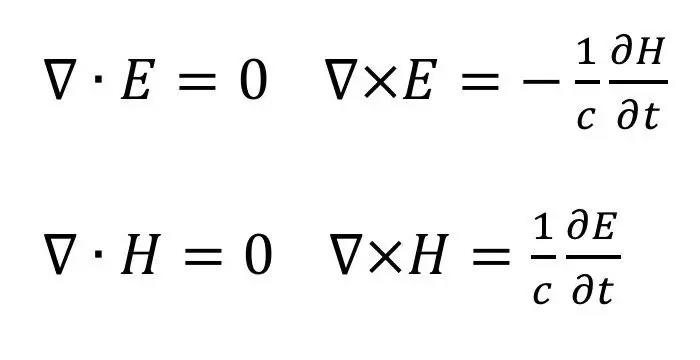
São as leis essenciais e fundamentais da física moderna.
Há 4 formas de equações matemáticas de Maxwell:
- Equação de Maxwell-Gauss: descreve como as cargas elétricas geram campos elétricos.
- Equação de Maxwell-Thomson: estabelece que não existem um único polo magnético (todo ímã tem um polo norte e um sul).
- Equação de Maxwell-Faraday: explica que um campo magnético muda com o tempo e cria um campo elétrico. Essa é a base dos geradores de energia.
- Equação de Maxwell-Ampère: descreve como correntes elétricas e campos elétricos variáveis criam campos magnéticos.
Na física avançada, essas leis são expressas através de equações complexas que utilizam o cálculo vetorial. Sem essas equações matemáticas, não teríamos desenvolvido as telecomunicações, o radar ou a televisão.
Segunda Lei da Termodinâmica: equação matemática complexa da desordem
A Segunda Lei da Termodinâmica (também conhecida como ciclo de Carnot difundida em 1824) prova de maneira irrefutável que os fenômenos físicos são irreversíveis, notadamente quando há mudanças térmicas. Enquanto outras leis da física funcional para frente e para trás, esta lei estabelece uma "seta no tempo" através de equações matemáticas que regem a energia.
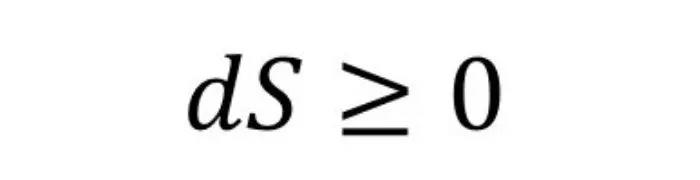
Esse princípio foi redesenhado e reformulado várias vezes. Ludwig Boltzmann e Max Planck o popularizaram em grande escala em 1873.
Enquanto a primeira lei da termodinâmica estabelece uma equivalência de diferentes formas de energia como o calor e o trabalho (princípio de conservação), a segunda lei introduz um outro sistema chamado entropia. Ela determina em qual direção as transformações energéticas podem ocorrer.
É um princípio de evolução porque ele determina em qual direção as possíveis transformações energéticas do mundo podem ser realizadas. Em consequência disso, algumas transformações químicas são possíveis enquanto outras nunca serão.
A grande revolução ocorreu quando o comportamento desordenado das partículas foi traduzido em uma fórmula. Ludwig Baltzmann criou uma equação matemática complexa que relaciona a entropia (S) com a probabilidade de estados moleculares:
S = k . 1nW
Concretamente, se você colocar um gelo em sua taça de café quente, você vai ver o gelo derreter mas nunca o café congelado, pois isso exigiria a violação dessas equações complexas. Essa teoria explica por que algumas transformações são possíveis e outras nunca ocorrerão espontaneamente.

Para aprender mais sobre as leis da termodinâmica, e como o calor e a energia moldam o nosso futuro, que tal um fazer curso de matematica basica?
A Equação de Schrödinger: o pilar da mecânica quântica
Se a gente devesse ilustrar o que são a matemática e a mecânica quântica, a equação de Schrödinger seria o exemplo perfeito. Criada pelo físico austríaco Erwin Schrödinger em 1925, essa equação matemática complexa é o alicerce fundamental para a compreensão do mundo em escala microscópica.
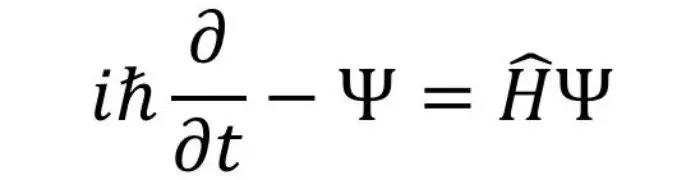
Como a teria da relatividade geral de Einstein pôde explicar o universo em grande escala, essa equação esclarece muito sobre o comportamento dos átomos e as partículas subatômicas. A equação de Schrödinger explica a evolução no tempo de uma partícula. Ela descreve os estados dessas partículas no momento em que é possível descrever todos os seus estados.
Essa equação deixa uma pergunta filosófica no ar: a matéria é constituída de presenças de estados possíveis (gaz, sólido, líquido)? Não há outra coisa? Mas não se engane, apesar de parecer abstrata, a aplicação prática dessa equação se encontra na tecnologia moderna como a energia nuclear, os computadores, a semicondução, a ressonância magnética e os lasers.
Bônus: Equações Matemáticas que moldam a modernidade
Como vimos, as equações matemáticas são sentenças de igualdade que contêm uma ou mais incógnitas, que são valores desconhecidos geralmente representados por letras, em que é buscado o valor dessas letras para que a igualdade seja verdadeira. Essas expressões representam um equilíbrio, exigindo que operações sejam feitas nos dois lados para achar a verdade, ou igualdade. São classificadas por grau e por tipo de incógnita (exponencial ou logarítmica).
Para além de todas essas equações complexas que mudaram os rumos da física e da matemática para sempre. existem outras fórmulas que regem o nosso sistema financeiro e a era da informação.
Vamos listar aqui mais duas equações matemáticas indispensáveis para quem quer aprofundar no universo de equações complexas:
- Equação de Black-Scholes: utilizada no mercado financeiro para calcular o preço de opções, essa equação matemática complexa revolucionou a economia moderna ao permitir a gestão de riscos em investimentos.
- A Teoria da informação de Shannon: essa fórmula é o coração da internet. Ela quantifica quantidade informação em um sinal, permitindo que os dados sejam transmitidos sem perdas por todo o mundo. É uma das equações matemáticas que tornam possível o streaming e as chamadas de vídeo, por exemplo.
Antes de 1557, os matemáticos escreviam "é igual a" por extenso. Foi o galês Robert Recorde que inventou o sinal =, argumentando que nada poderia ser mais igual do que duas linhas paralelas.
Como a gente pode ver através do tempo e principalmente no século XVIII e XIX, as equações matemáticas souberam transformar o mundo em que vivemos. Elas nos servem todos os dias no cotidiano, de maneira mais ou menos direta.
Historicamente, a transição entre o cálculo manual e o uso de equações complexas abstratas marcou o início de uma Revolução. A busca pela "Teoria de Tudo", uma equação matemática complexa única que unifique a gravidade de Einstein com a mecânica quântica de Schrödinger é o grande "Santo Graal" da ciência
Qual é a próxima inovação matemática? Quais são as novas revelações matemáticas que vão ainda mudar completamente a concepção de vida tal como a gente pensa? Com o avanço da Inteligência Artificial, estamos vendo o surgimento de algoritmos de Deep Learning que criam suas próprias equações complexas para resolver problemas que a mente humana não consegue processar sozinha.
Pode ficar tranquilo que a Superprof vai ficar atenta e vai te contar tudo!
Referências
- LUIZ, Robson. "Equação"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/equacao.htm. Acesso em 17 de janeiro de 2026.
- NETO, Francisco Miraglia. "Quais são as dez equações mais importantes da história?" Disponível em : https://super.abril.com.br/especiais/quais-sao-as-dez-equacoes-mais-importantes-da-historia/. Acesso em 17 de janeiro de 2026.
Resumir com IA:















Magnífico !
Maravilhoso artigo. Obrigada
Incrivel
Artigo objetivo e encantador.
Excelente!
Conhecer o comportamento dos números é conhecer o universo…
A intelectualidade é mágica!!!
Fascinante!