O termo geral de uma sequência é um critério que nos permite determinar qualquer termo da sequência, sendo representado por 
.
1. Verifique se a sequência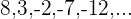 
é uma progressão aritmética.
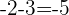
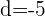
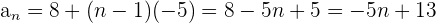
2. Verifique se a sequência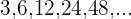 
é uma progressão geométrica.
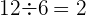
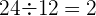
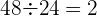
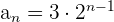
3. Verifique se os termos da sequência 
são quadrados perfeitos.
Observamos que as bases estão em progressão aritmética, sendo 
, e o expoente é constante:
Portanto, o termo geral é:
Também podemos encontrar sequências cujos termos são números próximos a quadrados perfeitos:
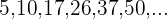
Encontramos o termo geral como no exemplo anterior e somamos 1:
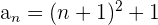
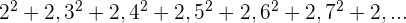
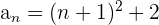
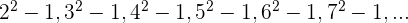
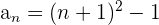
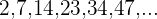
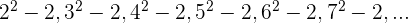
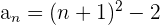
4. Os termos da sequência alternam de sinal consecutivamente.
Se os termos ímpares são negativos e os pares positivos: multiplicamos por 
.
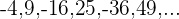
Se os termos ímpares são positivos e os pares negativos: multiplicamos por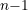 
.
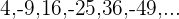
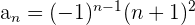
5. Se os termos da sequência são fracionários (não sendo uma progressão).
Calcula-se o termo geral do numerador e do denominador separadamente.
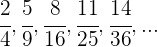
Temos duas sequências:
A primeira é uma progressão aritmética com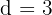 
, a segunda é uma sequência de quadrados perfeitos.
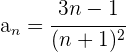
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
