Temas
- Regra de L'Hôpital
- Exercícios resolvidos da regra de L'Hôpital
- Formas de indeterminação em potências
- Exercícios resolvidos com indeterminações
- Exercícios resolvidos da indeterminação infinito menos infinito
- Indeterminação zero vezes infinito
- Exercícios resolvidos da indeterminação zero vezes infinito
- Exercícios diversos de indeterminações e regra de L'Hôpital
A regra de L'Hôpital é um importante teorema em cálculo diferencial utilizado para avaliar limites indeterminados de funções. Foi desenvolvida pelo matemático francês Guillaume de L'Hôpital no século XVIII. Esta regra fornece um método eficaz para calcular limites das formas 
ou 
, que são formas indeterminadas.
A regra de L'Hôpital é uma ferramenta muito útil para simplificar cálculos e resolver limites que, de outra forma, seriam difíceis de calcular. No entanto, é importante lembrar que ela se aplica apenas em situações específicas, onde determinadas condições necessárias são atendidas.
Regra de L'Hôpital
Se 
e 
são duas funções contínuas tais que
A regra de L'Hôpital diz o seguinte:
.
Para poder aplicar a regra de L'Hôpital, é necessário que o limite tenha a forma: 
, e que exista uma das seguintes indeterminações:
,
A seguir, alguns exercícios resolvidos para ajudar a entender melhor a aplicação da regra de L'Hôpital.
Exercícios resolvidos da regra de L'Hôpital
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e denominador do quociente. Calculamos o limite.
3 Obter o limite
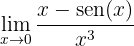
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e denominador do quociente. Calculamos o limite.
Obtemos novamente uma indeterminação, portanto, aplicaremos a regra de L'Hôpital mais uma vez:
E novamente:
3 Obter o limite
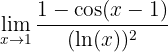
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e denominador do quociente. Calculamos o limite.
Aplicamos a regra novamente:
3 Obter o limite
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e denominador do quociente. Calculamos o limite:
Utilizamos a seguinte propriedade das funções trigonométricas: 
,
E aplicamos a regra de L'Hôpital mais uma vez:
3 Obter o limite
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e denominador do quociente. Calculamos o limite.
3 Obter o limite
Formas de indeterminação em potências
As formas indeterminadas 
, 
e 
ocorrem quando consideramos expressões da forma
Essas indeterminações são resolvidas primeiro aplicando as propriedades do logaritmo:
Dada a função:
Aplicando o logaritmo
Aplicando o exponencial
Logo:
Portanto, para resolver o limite original, basta obter o limite de seu logaritmo:
E, assim, o limite original será:
Exercícios resolvidos com indeterminações
1 Identificar a indeterminação
2 Calcular o limite do logaritmo
Temos a forma indeterminada 
3 Aplicar a regra de L'Hôpital
Forma indeterminada:
Aplicamos a regra de L'Hôpital novamente:
4 Obtemos o limite
Portanto:
E, então:
1 Identificar a indeterminação
2 Calculamos o limite do logaritmo
Temos a forma indeterminada 
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Então:
4 Obtemos o limite original
Portanto:
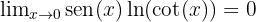
E, então:
1 Identificar a indeterminação
2 Calculamos o limite do logaritmo
Temos a forma indeterminada 
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Então:
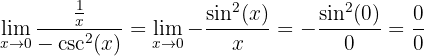
Aplicamos L'Hôpital de novo:
4 Obtemos o limite original
Portanto:
E assim:
1 Identificar a indeterminação
2 Calculamos o limite do logaritmo
Temos a forma indeterminada
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Então:
4 Obtemos o limite original
Portanto:
Assim:
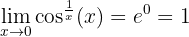
1 Identificar a indeterminação
2 Calculamos o limite do logaritmo
Temos a forma indeterminada
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
4 Obtemos o limite original
Portanto:
Assim:
Exercícios resolvidos da indeterminação infinito menos infinito
Nesses casos, devemos observar a "rapidez" com que as funções tendem ao infinito. Além disso, se forem frações, devemos colocá-las em denominadores comuns.
1 Identificar a indeterminação
2 Reescrever expressão
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Obtemos outra indeterminação e novamente, aplicamos a regra:
4 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Obtemos outra indeterminação e novamente, aplicamos a regra:
4 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Obtemos outra indeterminação e novamente, aplicamos a regra:
4 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Obtemos outra indeterminação e novamente, aplicamos a regra:
4 Obtemos o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
4 Obter o limite
Portanto:
Indeterminação zero vezes infinito
Essas formas de indeterminação podem ser transformadas em casos que já vimos, como ou .
Como mostrado a seguir, temos que:
onde 
e 
Então, podemos reescrever da seguinte forma, para facilitar a aplicação da derivada:
ou
Com isso, podemos usar a regra de L'Hôpital.
Exercícios resolvidos da indeterminação zero vezes infinito
1 Identificar a indeterminação
2 Reescrever a expressão
Indeterminação do tipo
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
4 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
Indeterminação do tipo
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
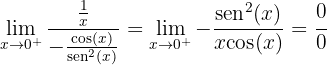
Aplicamos novamente, a regra de L'Hôpital:
4 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
Indeterminação do tipo
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
Novamente, aplicamos a regra de L'Hôpital
4 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
Reescrevemos de maneira conveniente para que seja possível aplicar a regra de L'Hôpital.
3 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
4 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Reescrever a expressão
Indeterminação do tipo
3 Aplicar regra de L'Hôpital
Ao derivar, obtemos
4 Obter o limite
Portanto:
Exercícios diversos de indeterminações e regra de L'Hôpital
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Ao derivar, obtemos:
3 Obter o limite
Portanto:
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e o denominador do quociente. Calculamos o limite:
3 Obter o limite
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e o denominador do quociente. Calculamos o limite:
3 Obter o limite
1 Identificar a indeterminação
2 Reformular o problema
Somente ao expressarmos de forma diferente seremos capazes de identificar as condições para aplicar a regra de L'Hôpital.
3 Aplicar a regra de L'Hôpital
Derivamos o numerador e o denominador do quociente. Calculamos o limite:
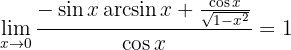
4 Obter o limite
1 Identificar a indeterminação
2 Calcular o limite do logaritmo
Temos a forma indeterminada
3 Aplicar a regra de L'Hôpital
Derivamos o numerador e o denominador do quociente. Calculamos o limite:
4 Obter o limite
1 Identificar a indeterminação
2 Calcular o limite do logaritmo
Temos a forma indeterminada
3 Aplicar a regra de L'Hôpital
Derivamos o numerador e o denominador do quociente. Calculamos o limite:
Aplicamos a regra de L'Hôpital novamente:
4 Obter o limite
1 Identificar a indeterminação
2 Aplicar a regra de L'Hôpital
Derivamos o numerador e o denominador do quociente. Calculamos o limite:
Aplicamos a regra de L'Hôpital de novo:
3 Obter o limite
1 Identificar a indeterminação
2 Reescrever a expressão
Indeterminação
3 Aplicar a regra de L'Hôpital
Aplicamos a regra de L'Hôpital outra vez:
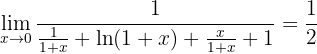
4 Obter o limite
1 Identificar a indeterminação
2 Calcular o limite do logaritmo
Temos a forma indeterminada
3 Aplicar a regra de L'Hôpital
4 Obter o limite original
1 Identificar a indeterminação
2 Calculamos o limite do logaritmo
Rescrevemos de modo conveniente:
Temos forma indeterminada:
3 Aplicar a regra de L'Hôpital
Aplicamos a regra de L'Hôpital novamente:
4 Obter o limite original
Gostou desse artigo? Deixe uma nota!
Loading...
