
O Teorema de Bayes
O Teorema de Bayes é um dos resultados mais conhecidos e úteis na área de probabilidade e estatística e em particular, no estudo da probabilidade condicional. Basicamente, o Teorema de Bayes nos diz como calcular a probabilidade de um evento, tendo informações a priori (anterior) sobre esse evento.
Este teorema é uma ferramenta amplamente utilizada devido à sua simplicidade e à facilidade de aplicação em diversas áreas do conhecimento, como medicina, biologia, tecnologia, negócios ou em qualquer campo, onde seja necessário obter certeza sobre um evento, com base nas informações prévias disponíveis. Além disso, é comum utilizar essa ferramenta de forma interativa, a fim de aumentar a precisão, sempre que o problema exigir uma maior assertividade.
A seguir, apresentaremos o enunciado do teorema e resolveremos alguns exercícios para ilustrar de forma prática este importante conceito.
Teorema de Bayes: Sejam  eventos mutuamente excludentes cuja união forme um espaço amostral
eventos mutuamente excludentes cuja união forme um espaço amostral  , ou seja,
, ou seja,

Se  é outro evento, então:
é outro evento, então:
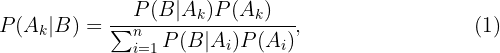
onde:
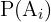 representa a probabilidade do evento
representa a probabilidade do evento  denominada como probabilidade a priori,
denominada como probabilidade a priori,
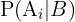 representa a probabilidade do evento
representa a probabilidade do evento  dado o evento
dado o evento  também conhecida como probabilidade a posteriori e
também conhecida como probabilidade a posteriori e
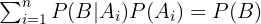 é a probabilidade total do evento
é a probabilidade total do evento 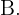 A equação (1) é conhecida como fórmula de Bayes.
A equação (1) é conhecida como fórmula de Bayes.
Exemplos resolvidos do Teorema de Bayes
Temos duas caixas: a primeira contém 3 bolas vermelhas e 2 azuis, e a segunda contém 2 vermelhas e 8 azuis. Lança-se uma moeda: se sair cara, retira-se uma bola da primeira caixa; se sair coroa, retira-se uma bola da segunda. Sabendo que a bola retirada é azul, qual a probabilidade de que ela venha da primeira caixa?
Considere os seguintes eventos e suas probabilidades:
-
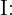 "A bola é retirada da caixa I"
"A bola é retirada da caixa I"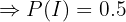
-
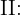 "A bola é retirada da caixa II"
"A bola é retirada da caixa II"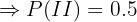
Além disso, considere o evento 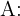 "A bola é azul". O exercício nos dá as seguintes probabilidades:
"A bola é azul". O exercício nos dá as seguintes probabilidades:

Estamos interessados em calcular 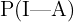 , ou seja, a probabilidade de que a bola tenha sido retirada da caixa I considerando que ela é azul. Aplicando a fórmula de Bayes, temos:
, ou seja, a probabilidade de que a bola tenha sido retirada da caixa I considerando que ela é azul. Aplicando a fórmula de Bayes, temos:

Utilizando os mesmos dados do exercício anterior, se sabemos que a bola obtida é vermelha, qual é a probabilidade de que ela tenha vindo da segunda caixa?
Considere os seguintes eventos e suas probabilidades:
-
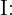 "A bola é retirada da caixa I"
"A bola é retirada da caixa I"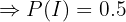
-
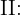 "A bola é retirada da caixa II"
"A bola é retirada da caixa II"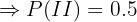
Além disso, considere o evento 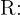 "A bola é vermelha". O exercício nos dá as seguintes probabilidades:
"A bola é vermelha". O exercício nos dá as seguintes probabilidades:

Estamos interessados em calcular P(II∣R)P(II|R) 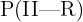 , ou seja, a probabilidade de que a bola tenha sido retirada da caixa II, considerando que ela é vermelha. Aplicando a fórmula de Bayes, temos:
, ou seja, a probabilidade de que a bola tenha sido retirada da caixa II, considerando que ela é vermelha. Aplicando a fórmula de Bayes, temos:

Temos duas caixas: a primeira contém 3 bolas vermelhas e 2 azuis, e a segunda contém 2 vermelhas e 8 azuis. Lança-se um dado: se sair 1 ou 2, retira-se uma bola da primeira caixa; se sair 3, 4, 5 ou 6, retira-se uma bola da segunda. Sabendo que a bola obtida é azul, qual a probabilidade de que ela tenha vindo da primeira caixa?
Considere os seguintes eventos e suas probabilidades:
-
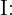 "A bola é retirada da caixa I"
"A bola é retirada da caixa I"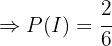
-
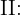 "A bola é retirada da caixa II"
"A bola é retirada da caixa II"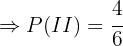
Além disso, considere o evento  "A bola é azul". O exercício nos dá as seguintes probabilidades:
"A bola é azul". O exercício nos dá as seguintes probabilidades:

Estamos interessados em calcular 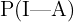 , ou seja, a probabilidade de que a bola tenha sido retirada da caixa I dado que ela é azul. Aplicando a fórmula de Bayes, temos:
, ou seja, a probabilidade de que a bola tenha sido retirada da caixa I dado que ela é azul. Aplicando a fórmula de Bayes, temos:
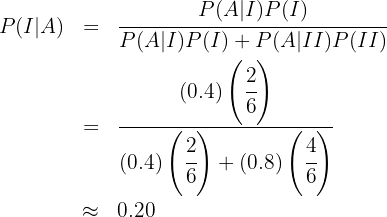
Em uma escola, 12% dos alunos utilizam IA para realizar seus trabalhos escolares. Um professor utiliza um detector de uso de IA que acerta 90% das vezes quando o trabalho foi feito com IA e falha 5% das vezes quando o trabalho não foi feito com IA. Se o professor recebe o resultado de que o trabalho foi realizado com IA, qual é a probabilidade de estar equivocado?
Considere os seguintes eventos e suas probabilidades:
-
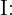 "O aluno utiliza IA"
"O aluno utiliza IA"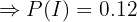
-
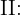 "O aluno não utiliza IA"
"O aluno não utiliza IA"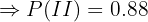
Além disso, considere o evento 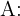 "A prova é afirmativa". O exercício nos dá as seguintes probabilidades:
"A prova é afirmativa". O exercício nos dá as seguintes probabilidades:
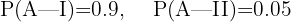
Estamos interessados em calcular  , ou seja, a probabilidade de que o aluno não tenha utilizado IA dado que a prova foi afirmativa. Aplicando a fórmula de Bayes, temos:
, ou seja, a probabilidade de que o aluno não tenha utilizado IA dado que a prova foi afirmativa. Aplicando a fórmula de Bayes, temos:

Em um restaurante de fast food, 30% dos clientes são crianças. Existem dois combos à venda, sendo o combo 1 escolhido por 60% das crianças e por 20% dos adultos. Se a ordem entregue for o combo 2, qual é a probabilidade de que o pedido seja de uma criança?
Considere os seguintes eventos e suas probabilidades:
-
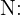 "O cliente é uma criança"
"O cliente é uma criança"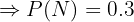
-
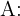 "O cliente é um adulto"
"O cliente é um adulto"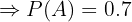
Além disso, considere o evento 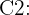 "A ordem é o combo 2". O exercício nos dá as seguintes probabilidades:
"A ordem é o combo 2". O exercício nos dá as seguintes probabilidades:

Estamos interessados em calcular 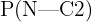 , ou seja, a probabilidade de que o pedido seja de uma criança dado que é o combo 2. Aplicando a fórmula de Bayes, temos:
, ou seja, a probabilidade de que o pedido seja de uma criança dado que é o combo 2. Aplicando a fórmula de Bayes, temos:

A probabilidade de que haja um acidente em uma fábrica com alarme  . A probabilidade de que o alarme toque se houve um incidente é
. A probabilidade de que o alarme toque se houve um incidente é 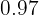 e a probabilidade de que o alarme toque se não houve incidente é
e a probabilidade de que o alarme toque se não houve incidente é  .Sabendo que o alarme tocou, qual é a probabilidade de que não tenha ocorrido um incidente?
.Sabendo que o alarme tocou, qual é a probabilidade de que não tenha ocorrido um incidente?
Considere os seguintes eventos e suas probabilidades:
-
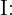 "O incidente ocorreu"
"O incidente ocorreu"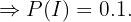
-
 "Não houve incidente"
"Não houve incidente"
Além disso, considere o evento 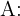 "O alarme tocou" e o evento
"O alarme tocou" e o evento 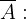 O alarme não tocou". O exercício nos dá as seguintes probabilidades:
O alarme não tocou". O exercício nos dá as seguintes probabilidades:

A informação anterior pode ser resumida no seguinte diagrama de árvore:
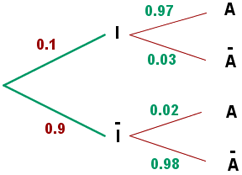
Estamos interessados em calcular 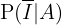 ,ou seja, a probabilidade de que não tenha ocorrido um incidente dado que o alarme tocou. Aplicando a fórmula de Bayes, temos:
,ou seja, a probabilidade de que não tenha ocorrido um incidente dado que o alarme tocou. Aplicando a fórmula de Bayes, temos:
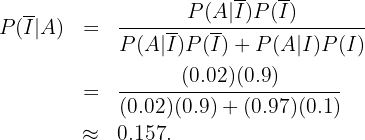
O laboratório tem uma eficácia de 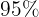 para detectar uma doença quando ela está realmente presente. No entanto, o teste também apresenta um "falso positivo" para
para detectar uma doença quando ela está realmente presente. No entanto, o teste também apresenta um "falso positivo" para 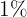 das pessoas saudáveis analisadas. (Ou seja, se é feita um teste com uma pessoa saudável, então, a probabilidade é
das pessoas saudáveis analisadas. (Ou seja, se é feita um teste com uma pessoa saudável, então, a probabilidade é 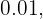 do resultado que o teste implicará que tem a doença). Se
do resultado que o teste implicará que tem a doença). Se 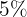 da população realmente tem a doença, qual é a probabilidade de que uma pessoa tenha a doença, dado que o teste foi positivo?
da população realmente tem a doença, qual é a probabilidade de que uma pessoa tenha a doença, dado que o teste foi positivo?
Considere o evento:
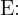 "Tem a doença" cuja probabilidade é:
"Tem a doença" cuja probabilidade é: 
e o evento:
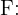 "O resultado é positivo".
"O resultado é positivo".
Sabemos que o laboratório tem uma eficácia de 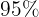 para detectar uma determinada doença, assim, temos que:
para detectar uma determinada doença, assim, temos que:
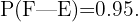
Agora, considere o evento:
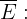 "Não tem a doença"
"Não tem a doença"
cuja probabilidade é:
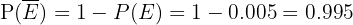
e o evento:
 "O resultado é negativo".
"O resultado é negativo".
As hipóteses indicam que:

Queremos calcular  , ou seja, a probabilidade de que a pessoa tenha a doença, considerando que o teste foi positivo. Aplicando a fórmula de Bayes, temos:
, ou seja, a probabilidade de que a pessoa tenha a doença, considerando que o teste foi positivo. Aplicando a fórmula de Bayes, temos:
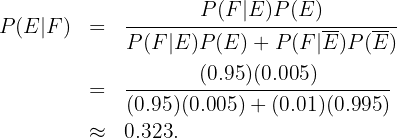
Em uma investigação criminal, o investigador está convencido de que a probabilidade de culpa de um suspeito é  . No entanto, uma nova evidência mostra que o suspeito tem uma característica específica que
. No entanto, uma nova evidência mostra que o suspeito tem uma característica específica que  da população possui. Qual é a probabilidade de que o suspeito seja culpado, dado que ele tem essa característica?
da população possui. Qual é a probabilidade de que o suspeito seja culpado, dado que ele tem essa característica?
Considere o evento:
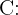 "O suspeito é culpado"
"O suspeito é culpado"
cuja probabilidade, conforme o exercício, é 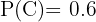 . Também, considere o evento:
. Também, considere o evento:
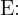 "Coincide com a evidência de alguém inocente".
"Coincide com a evidência de alguém inocente".
Das hipóteses, temos que 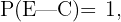 ou seja, alguém que tenha a evidência, será considerado culpado, sempre será verdadeiro. Além disso, se o evento:
ou seja, alguém que tenha a evidência, será considerado culpado, sempre será verdadeiro. Além disso, se o evento:
 "O suspeito é inocente",
"O suspeito é inocente",
portanto:
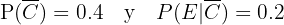
Queremos calcular 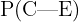 ou seja, a probabilidade de que o suspeito seja culpado dado que ele tem a característica. Aplicando a fórmula de Bayes, temos:
ou seja, a probabilidade de que o suspeito seja culpado dado que ele tem a característica. Aplicando a fórmula de Bayes, temos:
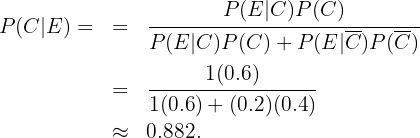
Uma fábrica de pregos tem  máquinas que fabricam
máquinas que fabricam  e
e  dos pregos. A probabilidade de pregos defeitusos de cada máquina é de
dos pregos. A probabilidade de pregos defeitusos de cada máquina é de  e
e  , respectivamente. Se um prego defeituoso é escolhido aleatoriamente, qual a probabilidade de que ele tenha sido fabricado pela máquina
, respectivamente. Se um prego defeituoso é escolhido aleatoriamente, qual a probabilidade de que ele tenha sido fabricado pela máquina  ?
?
Considere os seguintes eventos e suas probabilidades:
-
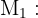 "Pregos fabricados pela máquina
"Pregos fabricados pela máquina  "
"
-
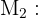 "Pregos fabricados pela máquina
"Pregos fabricados pela máquina  "
"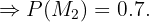
-
 "Prego fabricados são defeituosos"
"Prego fabricados são defeituosos" 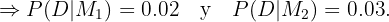
Queremos calcular 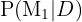 ,ou seja, a probabilidade de que o prego selecionado aleatoriamente tenha sido fabricado pela máquina
,ou seja, a probabilidade de que o prego selecionado aleatoriamente tenha sido fabricado pela máquina  dado que ele é defeituoso. Aplicando a fórmula de Bayes, temos:
dado que ele é defeituoso. Aplicando a fórmula de Bayes, temos:

Em uma empresa,  dos empregados são engenheiros e
dos empregados são engenheiros e  são economistas.
são economistas. 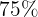 dos engenheiros ocupam cargos de liderança e
dos engenheiros ocupam cargos de liderança e  dos economistas também. Enquanto os outros empregados (nem engenheiros, nem economistas) têm apenas
dos economistas também. Enquanto os outros empregados (nem engenheiros, nem economistas) têm apenas  de chance de ocupar cargos de liderança. Qual é a probabilidade de que um empregado diretor escolhido aleatoriamente seja engenheiro?
de chance de ocupar cargos de liderança. Qual é a probabilidade de que um empregado diretor escolhido aleatoriamente seja engenheiro?
Considere os seguintes eventos e suas probabilidades:
-
 "O empregado é engenheiro"
"O empregado é engenheiro" 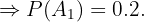
-
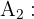 "O empregado é economista"
"O empregado é economista" 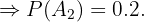
-
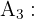 "O empregado tem outra formação"
"O empregado tem outra formação"
Além disso, considere o evento 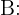 "O empregado ocupa um cargo de liderança". O exercício nos dá as seguintes probabilidades:
"O empregado ocupa um cargo de liderança". O exercício nos dá as seguintes probabilidades:

A informação anterior pode ser resumida no diagrama de árvore abaixo:

Queremos calcular 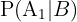 , ou seja, a probabilidade de que um empregado seja engenheiro dado que sabemos que ele ocupa um cargo de liderança. Aplicando a fórmula de Bayes, temos:
, ou seja, a probabilidade de que um empregado seja engenheiro dado que sabemos que ele ocupa um cargo de liderança. Aplicando a fórmula de Bayes, temos:
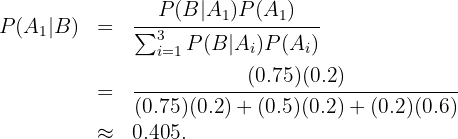
Resumir com IA:












