Formando números usando dígitos
Quantos números com 5 cifras diferentes podemos formar com os dígitos: 1, 2, 3, 4 e 5?
1. Estabelecemos as condições do exercício:
Sim entram todos os elementos. De 5 dígitos entram apenas 3
Sim importa a ordem. São números diferentes o 123, 231, 321
Não se repetem os elementos. O enunciado nos pede que as cifras sejam diferentes
2. Trata-se de uma permutação, por isso utilizamos a fórmula:
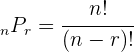

3. Substituímos e resolvemos:

Acomodando pessoas em assentos
De quantas maneiras podem se sentar oito pessoas em uma fileira de assentos?
De quantas maneiras podem se sentar oito pessoas em uma fileira de assentos?
1. Estabelecemos as condições do exercício:
Sim, entram todos os elementos. Podem se sentar 8 pessoas
Sim, importa a ordem
Não se repetem os elementos. Uma pessoa não pode ser repetida
2. Trata-se de uma permutação, por isso utilizamos a fórmula:
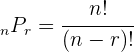

3. Substituímos e resolvemos:
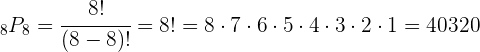
Pessoas ao redor de uma mesa redonda
De quantas maneiras podem se sentar oito pessoas ao redor de uma mesa redonda?
De quantas maneiras podem se sentar oito pessoas ao redor de uma mesa redonda?
1. Estabelecemos as condições do exercício:
Sim, entram todos os elementos. Podem se sentar 8 pessoas
Por estar organizada de maneira circular devemos eliminar as repetições circulares
Não se repetem os elementos. Uma pessoa não pode ser repetida
2. Trata-se de uma combinação, por isso utilizamos a fórmula:
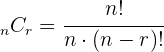

3. Substituímos e resolvemos:
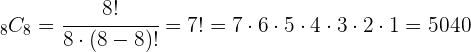
Formando números usando cifras
Com as cifras 2, 2, 2, 3, 3, 3, 3, 4, 4;
Quantos números de nove cifras podem ser formados?
1. Temos 3 elementos a, b e c que se repetem:

2. Trata-se de uma permutação com vários elementos que se repetem, por isso usamos a fórmula:

3. Substituímos na fórmula e resolvemos:

Permutação com letras
Com as letras da palavra livro.
Quantas ordenações diferentes podem ser feitas que começam por uma vogal?
1. A palavra começa por i ou o seguida das 4 letras restantes colocadas de 4 em 4.
2. Estabelecemos as condições:
Sim, entram todos os elementos
Sim, importa a ordem
Não se repetem os elementos
3. Por ter duas vogais com as quais podem iniciar-se, podemos calcular o resultado com:


Crie permutações de 5 cifras
Quantos números diferentes de cinco cifras podemos formar usando as cifras ímpares?
Quantos deles são maiores que 70.000?
1. Estabelecemos as condições:
Sim, entram todos os elementos
Sim, importa a ordem
Não se repetem os elementos
2. Para encontrar os números de cinco cifras usando os dígitos ímpares (1, 3, 5, 7, 9) usamos a seguinte fórmula:
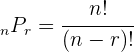
Substituímos e resolvemos:

Para encontrar os números que sejam maiores que 70.000 consideramos aqueles que comecem com 7 ou 8

Exercícios de mensagens com bandeiras
Em um mastro de um barco podem ser hasteadas três bandeiras vermelhas, duas azuis e quatro verdes.
Quantos sinais diferentes podem ser indicados com o hasteamento das nove bandeiras?
1. Temos 3 elementos a, b e c que se repetem:

2. Trata-se de uma permutação com vários elementos que se repetem, por isso usamos a fórmula:

3. Substituímos na fórmula e resolvemos:
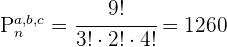
Quadro esportivo de futebol
De quantas formas podem ser colocados os 11 jogadores de uma equipe de futebol tendo em conta que o goleiro não pode ocupar outra posição além do gol?
1. Estabelecemos as condições do exercício:
Dispomos de 10 jogadores que podem ocupar 10 posições diferentes.
Sim, entram todos os elementos
Sim, importa a ordem
Não se repetem os elementos
2. Trata-se de uma permutação, por isso utilizamos a fórmula:
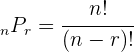

3. Substituímos e resolvemos:
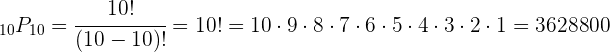
Problema de permutação com restrição
Uma mesa presidencial está formada por oito pessoas
De quantas maneiras eles podem se sentar tendo em conta que o presidente e o secretário vão sempre juntos?
1. Consideramos as duas pessoas que vão juntas como apenas uma, do qual conseguimos de duas maneiras. Agora há sete pessoas que podem se sentar ao redor da mesa, que cumpre:
Sim, entram todos os elementos
Sim, importa a ordem
Não se repetem os elementos
2. Podemos resolver o exercício com:
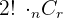
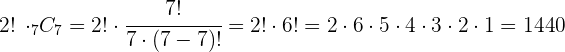
Calcule quantas maneiras existem de organizar os livros
Quatro diferentes livros de matemática, seis diferentes livros de física e dois diferentes livros de química são colocados em uma estante.
De quantas maneiras é possível organizá-los se:
A. Os livros de cada matéria devem estar todos juntos.
B. Apenas os livros de matemática devem estar juntos.
A. Os livros de cada matéria devem estar todos juntos.
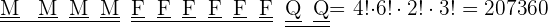
B. Apenas os livros de matemática devem estar juntos.
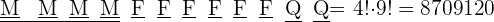
Organizando esferas
É organizada uma fileira de 5 bolas vermelhas, 2 bolas brancas e 3 bolas azuis.
Se as bolas de uma mesma cor não se distinguem entre si.
De quantas maneiras é possível organizá-las?
1. Temos 3 elementos a, b e c que se repetem:

2. Trata-se de uma permutação com vários elementos que se repetem, por isso usamos a fórmula:

3. Substituímos na fórmula e resolvemos:
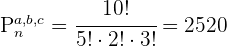
Resolva as equações
1. 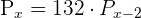
2. 
3. 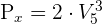
1. 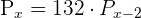
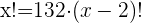
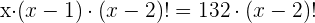
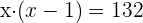
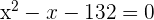

Descartamos a solução negativa, assim 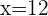
2. 

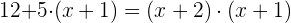
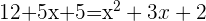


Descartamos a solução negativa, assim 
3. 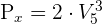
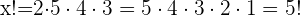
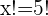

Resumir com IA:


