De um baralho de  cartas, extraímos simultaneamente duas cartas.
cartas, extraímos simultaneamente duas cartas.
Calcule a probabilidade de que:
- As duas sejam copas
- Ao menos uma seja copa
- Uma seja copa e a outra espada
a) As duas sejam copas
Podemos tratar este problema como se estivéssemos realizando duas extrações sem devolução.
Expressamos com  o evento em que obtemos uma copa na extração
o evento em que obtemos uma copa na extração  -ésima, com
-ésima, com 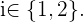 Com isso em mente e de acordo com a definição de probabilidade condicional.
Com isso em mente e de acordo com a definição de probabilidade condicional.
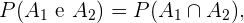
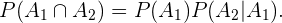
Para calcular 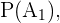 simplesmente dividimos o número de casos favoráveis entre o número de casos totais. Neste caso, há 12 cartas de copas entre as possibilidades, isso é, 12 é o número de casos favoráveis. E um total de 48 cartas, que representam o número de casos totais. Assim
simplesmente dividimos o número de casos favoráveis entre o número de casos totais. Neste caso, há 12 cartas de copas entre as possibilidades, isso é, 12 é o número de casos favoráveis. E um total de 48 cartas, que representam o número de casos totais. Assim
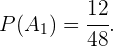
Por outro lado,
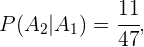
porque o número de casos favoráveis é 11, uma vez que já extraímos uma copa e o total de cartas é agora 47.
Logo,
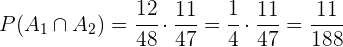
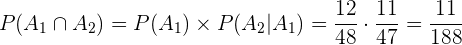
b) Ao menos uma seja copa
Expressamos com  o evento em que obtemos uma copa na extração
o evento em que obtemos uma copa na extração 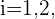 e com
e com 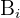 o evento em que não obtemos uma copa na extração
o evento em que não obtemos uma copa na extração  A condição de extrair ao menos uma copa será satisfeita em qualquer um dos seguintes casos:
A condição de extrair ao menos uma copa será satisfeita em qualquer um dos seguintes casos:
obtemos uma copa em ambas extrações,
obtemos uma copa na primeira extração e não obtemos copa na segunda, e
não obtemos uma copa na primeira extração e obtemos uma copa na segunda.
Então a probabilidade solicitada será a probabilidade da união dos três eventos anteriores, que é equivalente à soma de suas probabilidades, pois são eventos distantes entre si. Em termos matemáticos: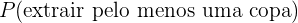

Pelo inciso anterior sabemos que 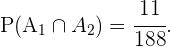
Para calcular as probabilidades restantes faremos uso da probabilidade condicional. Obtemos: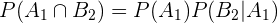
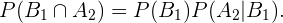
O número de casos favoráveis no evento 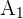 é 12 e no evento
é 12 e no evento 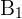 é 36, pois é o número de cartas que não são copas. Em ambos os casos, por ser a primeira extração, o número de casos totais continua sendo 48. Portanto:
é 36, pois é o número de cartas que não são copas. Em ambos os casos, por ser a primeira extração, o número de casos totais continua sendo 48. Portanto:
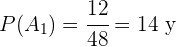
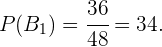
Assim, o número de casos favoráveis no evento 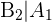 são 36, já que esse é o número de cartas que não são copas, enquanto que para
são 36, já que esse é o número de cartas que não são copas, enquanto que para 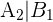 são 12, pois ainda não foi extraída nenhuma copa. Em ambos os casos o número de casos totais é 47, levando em conta que já foi tirada uma carta. Portanto:
são 12, pois ainda não foi extraída nenhuma copa. Em ambos os casos o número de casos totais é 47, levando em conta que já foi tirada uma carta. Portanto:
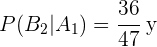
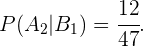
Então:
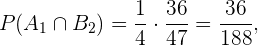
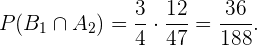
Assim,
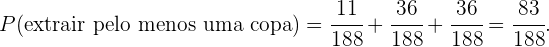
c) Uma seja copa e a outra espada
Chamamos  o evento em que obtemos uma copa na extração
o evento em que obtemos uma copa na extração 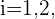 e como
e como 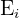 o evento em que não obtemos uma espada na extração
o evento em que não obtemos uma espada na extração  A condição de extrair uma copa e uma espada é satisfeita em qualquer um dos seguintes casos:
A condição de extrair uma copa e uma espada é satisfeita em qualquer um dos seguintes casos:
obtemos uma copa na primeira extração e uma espada na segunda, e
obtemos uma espada na primeira extração e uma copa na segunda.
Então a probabilidade que procuramos será a probabilidade da união dos três eventos anteriores, que é equivalente à soma de suas probabilidades, pois são eventos distantes entre si. Em termos matemáticos:
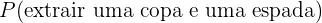
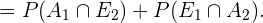
Por sua vez,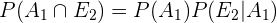
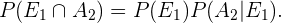
Como há 12 cartas de cada naipe no baralho e o baralho tem um total de 48 cartas, usando a fórmula de número de casos favoráveis entre os casos totais, compreendemos que,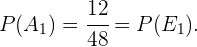
Por outro lado, no caso do evento 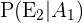 temos 12 casos favoráveis e um total de 47 cartas (pois já foi feita uma extração) ou casos totais. Devemos notar que são as mesmas contas para
temos 12 casos favoráveis e um total de 47 cartas (pois já foi feita uma extração) ou casos totais. Devemos notar que são as mesmas contas para 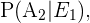 portanto:
portanto: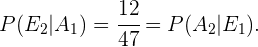
Com isso, obtemos: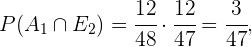
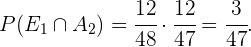
Por fim,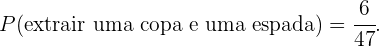
Para um exame, um aluno estudou apenas  dos
dos  temas correspondentes à matéria deste. O exame é composto de dois temas do quais o aluno poderá escolher apenas um para ser avaliado.
temas correspondentes à matéria deste. O exame é composto de dois temas do quais o aluno poderá escolher apenas um para ser avaliado.
Encontre a probabilidade de que o aluno possa escolher um dos temas estudados.
Chamamos  o evento “o aluno pode escolher um dos temas estudados”. Assim, temos
o evento “o aluno pode escolher um dos temas estudados”. Assim, temos
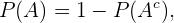
onde 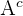 indica o evento complementar de
indica o evento complementar de  isto é, “o aluno pode escolher um dos temas estudados”.
isto é, “o aluno pode escolher um dos temas estudados”.
Para calcular 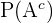 devemos lembrar que há 10 temas dos quais o aluno não estudou, por essa razão, a probabilidade de escolher como primeiro tema algum deles é igual a
devemos lembrar que há 10 temas dos quais o aluno não estudou, por essa razão, a probabilidade de escolher como primeiro tema algum deles é igual a 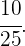 Simplesmente aplicamos a regra
Simplesmente aplicamos a regra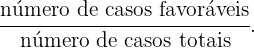
Da mesma maneira, a probabilidade de escolher como segundo tema algum dos quais o aluno não estudou é 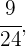 pois neste caso já escolhemos anteriormente um tema não estudado, o que nos deixa com
pois neste caso já escolhemos anteriormente um tema não estudado, o que nos deixa com  casos possíveis e
casos possíveis e  casos totais.
casos totais.
Assim, o resultado de 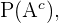 é multiplicar as duas probabilidades que encontramos pois presumimos que é equivalente à extrair sem repor dois temas não estudados, portanto:
é multiplicar as duas probabilidades que encontramos pois presumimos que é equivalente à extrair sem repor dois temas não estudados, portanto: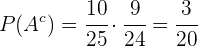
Então,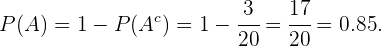
Uma turma está composta de  meninos e
meninos e  meninas; a metade das meninas e a metade dos meninos escolheram francês como matéria optativa.
meninas; a metade das meninas e a metade dos meninos escolheram francês como matéria optativa.
- Qual a probabilidade de que uma pessoa escolhida ao acaso seja menino ou que estudou francês?
- Qual a probabilidade de que seja menina e não estude francês?
a) Qual a probabilidade de que uma pessoa escolhida ao acaso seja menino ou que estudou francês?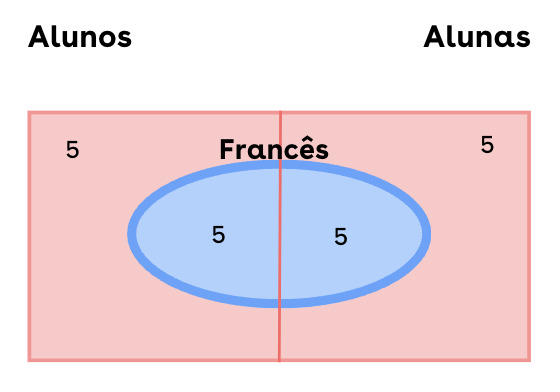
Vamos chamar  o evento “a pessoa escolhida ao azar é menino e não escolheu francês” e
o evento “a pessoa escolhida ao azar é menino e não escolheu francês” e  o evento “a pessoa escolhida ao azar estuda francês”. Então, se
o evento “a pessoa escolhida ao azar estuda francês”. Então, se  indica o evento “a pessoa escolhida ao acaso é menino ou estuda francês”, é a probabilidade que queremos calcular
indica o evento “a pessoa escolhida ao acaso é menino ou estuda francês”, é a probabilidade que queremos calcular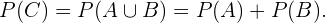
A última igualdade é certa já que os eventos  e
e  são distantes.
são distantes.
Para calcular  aplicamos a regra
aplicamos a regra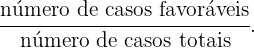
No evento  o número de casos favoráveis é
o número de casos favoráveis é  pois este é o número de pessoas que compreendem os grupos serem meninos e os que não estudam francês, enquanto que para
pois este é o número de pessoas que compreendem os grupos serem meninos e os que não estudam francês, enquanto que para  o número de pessoas que estuda francês é igual a
o número de pessoas que estuda francês é igual a  que é o número de casos favoráveis.
que é o número de casos favoráveis.
Em ambos os eventos o número de casos totais é 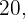 que é o número total de alunos.
que é o número total de alunos.
Com isso podemos concluir que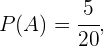
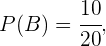
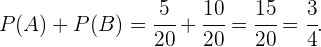
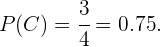
b) Qual a probabilidade de que seja menina e não estude francês?
No contexto do inciso anterior, basta observar que o evento “escolher ao acaso uma menina que não estude francês” é equivalente a  ou seja, é o evento complementar de
ou seja, é o evento complementar de 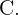
Para qualquer evento e seu complemento, as seguintes igualdades são válidas já que estes são sempre distantes.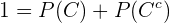
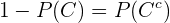
Então, substituindo o valor que encontramos no inciso anterior para 
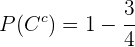
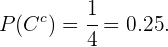
Em uma turma em que todos praticam algum esporte,  % dos alunos jogam futebol ou basquete e
% dos alunos jogam futebol ou basquete e  % praticam ambos os esportes.
% praticam ambos os esportes.
Além disso,  % não joga futebol.
% não joga futebol.
Qual será a probabilidade de que se escolhemos ao acaso um aluno desta turma este:
- Jogue apenas futebol
- Jogue apenas basquete
- Pratique apenas um destes esportes
- Não jogue nem futebol e nem basquete
a) Jogue apenas futebol
Sabemos que 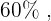 dos alunos jogam futebol ou basquete e que dessa porcentagem há
dos alunos jogam futebol ou basquete e que dessa porcentagem há 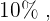 que praticam ambos os esportes. Isto quer dizer que
que praticam ambos os esportes. Isto quer dizer que  dos alunos praticam apenas um dos esportes, o que significa que a probabilidade de escolhermos um aluno que pratique apenas um dos esportes é igual a 0.5.
dos alunos praticam apenas um dos esportes, o que significa que a probabilidade de escolhermos um aluno que pratique apenas um dos esportes é igual a 0.5.
Por outro lado, 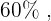 destes, ou a probabilidade de
destes, ou a probabilidade de 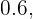 , não jogam futebol. Isso quer dizer que dos
, não jogam futebol. Isso quer dizer que dos  que praticam apenas um esporte,
que praticam apenas um esporte, 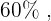 jogam apenas basquete. Agora,
jogam apenas basquete. Agora, 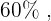 dos
dos  encontramos fazendo o produto
encontramos fazendo o produto 
Portanto, se  é o evento "jogar apenas futebol” e
é o evento "jogar apenas futebol” e  “jogar apenas basquete” e
“jogar apenas basquete” e  “praticar apenas um dos esportes”, então:
“praticar apenas um dos esportes”, então:
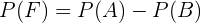
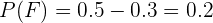
b) Jogue apenas basquete
Sabemos que  dos alunos jogam futebol ou basquete e que dessa porcentagem há
dos alunos jogam futebol ou basquete e que dessa porcentagem há 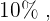 que praticam ambos os esportes. Isto quer dizer que
que praticam ambos os esportes. Isto quer dizer que  dos alunos praticam apenas um dos esportes, o que significa que a probabilidade de escolhermos um aluno que pratique apenas um dos esportes é igual a 0.5.
dos alunos praticam apenas um dos esportes, o que significa que a probabilidade de escolhermos um aluno que pratique apenas um dos esportes é igual a 0.5.
Por outro lado, 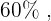 destes, ou a probabilidade de
destes, ou a probabilidade de 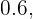 , não jogam futebol. Isso quer dizer que dos
, não jogam futebol. Isso quer dizer que dos  que praticam apenas um esporte,
que praticam apenas um esporte,  jogam apenas basquete. Agora,
jogam apenas basquete. Agora,  dos
dos  encontramos fazendo o produto
encontramos fazendo o produto 
Portanto, se  é o evento “jogar apenas basquete”, então:
é o evento “jogar apenas basquete”, então: 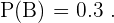
c) Pratique apenas um dos esportes
Sabemos que  dos alunos jogam futebol ou basquete e que dessa porcentagem há
dos alunos jogam futebol ou basquete e que dessa porcentagem há 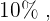 que praticam ambos os esportes. Isto quer dizer que
que praticam ambos os esportes. Isto quer dizer que  dos alunos praticam apenas um dos esportes, o que significa que a probabilidade de escolhermos um aluno que pratique apenas um dos esportes é igual a 0.5.
dos alunos praticam apenas um dos esportes, o que significa que a probabilidade de escolhermos um aluno que pratique apenas um dos esportes é igual a 0.5.
d) Não jogue nem futebol e nem basquete
Vamos chamar  o evento “jogam futebol” e
o evento “jogam futebol” e  o evento “jogam basquete”. Então “jogar futebol" ou "jogar basquete” é equivalente ao evento
o evento “jogam basquete”. Então “jogar futebol" ou "jogar basquete” é equivalente ao evento 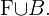 Então, a probabilidade de escolhermos alguém que não jogue futebol é igual a probabilidade do evento complementar de
Então, a probabilidade de escolhermos alguém que não jogue futebol é igual a probabilidade do evento complementar de 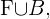 do qual sim conhecemos a probabilidade, pois hipoteticamente
do qual sim conhecemos a probabilidade, pois hipoteticamente 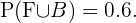
Assim,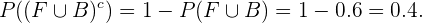
Uma oficina sabe que em média atendem pela manhã três automóveis com problemas elétricos, oito com problemas mecânicos e três com problemas na carroceria. E pela tarde, dois com problemas elétricos, três com problemas mecânicos e um com problemas na carroceria.
- Faça uma tabela organizando os dados anteriores
- Calcule a porcentagem dos que são atendidos pela tarde
- Calcule a porcentagem dos que são atendidos por causa de problemas mecânicos
- Calcule a probabilidade de que um automóvel com problemas elétricos seja atendido pela manhã
a) Faça uma tabela organizando os dados anteriores
| Horário | Problemas elétricos | Problemas mecânicos | Problemas de chapa |
|---|---|---|---|
| Manhã | 3 | 8 | 3 |
| Tarde | 2 | 3 | 1 |
b) Calcule a porcentagem dos que são atendidos pela tarde
Para calcular a porcentagem dos carros que são atendidos pela tarde, temos que simplesmente encontrar o quociente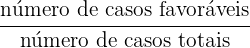
Nesta situação, o número de casos favoráveis é o número de carros que vão à oficina pela tarde, ou seja, 6; enquanto que o número de casos totais é o total de carros que comparecem, ou seja, 20.
Portanto,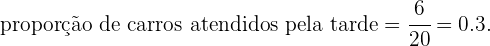
Por fim, para expressar esta cifra em porcentagem, temos apenas que multiplicá-la por cem. Então a porcentagem de carros que vão pela tarde é de 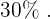
c) Calcule a porcentagem dos que comparecem por problemas mecânicos
Para calcular a porcentagem dos carros que vão pela tarde, temos que simplesmente encontrar o quociente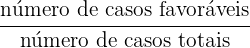
Nesta situação, o número de casos favoráveis é o número total de carros que vão à oficina por causa de problemas mecânicos, ou seja, 11; enquanto que o número de casos totais é o total de carros que comparecem à oficina, ou seja, 20.
Portanto,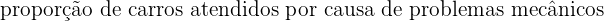
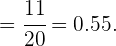
Por fim, para expressar esta cifra em porcentagem, temos apenas que multiplicá-la por cem. Então a porcentagem de carros que vão pela tarde é de 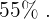
d) Calcule a probabilidade de que um automóvel com problemas elétricos vá pela manhã.
Para calcular a porcentagem de carros com problemas elétricos que vão à oficina temos que simplesmente encontrar o quociente.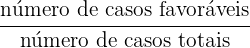
Nesta situação, o número de casos favoráveis é o número total de carros que comparecem à oficina por causa de problemas elétricos durante a parte da manhã, isto é, 3; enquanto que o número de casos totais é o total de carros que comparecem por problemas elétricos, ou seja, 5.
Portanto,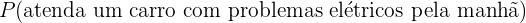
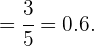
Em uma cidade,  da população têm cabelos castanhos,
da população têm cabelos castanhos,  têm olhos castanhos e
têm olhos castanhos e  têm cabelos e olhos castanhos.
têm cabelos e olhos castanhos.
Uma pessoa é escolhida ao acaso:
- Se tem cabelos castanhos, qual é a probabilidade de que tenha também olhos castanhos?
- Se tem olhos castanhos, qual é a probabilidade de que não tenha cabelos castanhos?
- Qual é a probabilidade de que não tenha cabelos castanhos e nem olhos castanhos?
a) Se tem cabelos castanhos, qual é a probabilidade de que tenha também olhos castanhos?


Indicamos com  os eventos “ter olhos castanhos” e “ter cabelo castanho”, respectivamente. Assim, a probabilidade que estamos procurando será expressada como
os eventos “ter olhos castanhos” e “ter cabelo castanho”, respectivamente. Assim, a probabilidade que estamos procurando será expressada como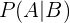
Com definição de probabilidade condicional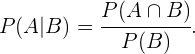
Observe que 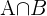 é equivalente a “ter olhos castanhos e cabelo castanho” do qual conhecemos sua probabilidade, pois
é equivalente a “ter olhos castanhos e cabelo castanho” do qual conhecemos sua probabilidade, pois  cumpre esta condição, isto é
cumpre esta condição, isto é 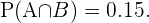 Seguindo este raciocínio, sabemos que
Seguindo este raciocínio, sabemos que 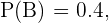 portanto,
portanto,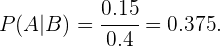
b) Se tem olhos castanhos, qual é a probabilidade de que não tenha cabelos castanhos?
De acordo com o enunciado,  têm olhos castanhos
têm olhos castanhos  têm cabelos e olhos castanhos, e os
têm cabelos e olhos castanhos, e os  restantes têm olhos castanhos, mas não têm os cabelos castanhos.
restantes têm olhos castanhos, mas não têm os cabelos castanhos.
Assim  são os eventos “não ter cabelos castanhos” e “ter olhos castanhos” respectivamente, então sabemos com o parágrafo anterior que o evento
são os eventos “não ter cabelos castanhos” e “ter olhos castanhos” respectivamente, então sabemos com o parágrafo anterior que o evento 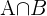 (equivalente a “ter olhos castanhos e não ter cabelos castanhos) têm probabilidade de
(equivalente a “ter olhos castanhos e não ter cabelos castanhos) têm probabilidade de  Como além disso sabemos que
Como além disso sabemos que  têm olhos castanhos, então
têm olhos castanhos, então 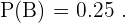
Portanto, com a definição de probabilidade condicional,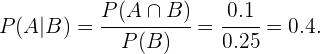
c) Qual é a probabilidade de que não tenha cabelos castanhos e nem olhos castanhos?
De acordo com o enunciado,  têm olhos castanhos,
têm olhos castanhos,  têm cabelos e olhos castanhos, e os
têm cabelos e olhos castanhos, e os  restantes têm olhos castanhos, mas não têm os cabelos castanhos.
restantes têm olhos castanhos, mas não têm os cabelos castanhos.
Por outro lado, sabemos que  da população têm cabelos castanhos, do qual podemos inferir que
da população têm cabelos castanhos, do qual podemos inferir que  restante não têm cabelos castanhos. Além disso, sabemos que
restante não têm cabelos castanhos. Além disso, sabemos que  não têm cabelos castanhos, mas têm olhos castanhos, então subtraindo-o pela porcentagem total da população sem cabelos castanhos, veremos que
não têm cabelos castanhos, mas têm olhos castanhos, então subtraindo-o pela porcentagem total da população sem cabelos castanhos, veremos que  da população não têm nem cabelos castanhos e nem olhos castanhos. Portanto, a probabilidade de escolher uma pessoa sem cabelos castanhos e sem olhos castanhos é de
da população não têm nem cabelos castanhos e nem olhos castanhos. Portanto, a probabilidade de escolher uma pessoa sem cabelos castanhos e sem olhos castanhos é de 
Em uma turma há  alunos, dos quais:
alunos, dos quais:  são homens,
são homens,  usam óculos e
usam óculos e  são homens e usam óculos.
são homens e usam óculos.
- Qual é a probabilidade de que seja mulher e não use óculos?
- Se sabemos que o aluno selecionado não usa óculos, qual a probabilidade de que seja homem?
a) Qual é a probabilidade de que seja mulher e não use óculos?
Há 100 alunos, dos quais 40 são homens, o que significa que 60 são mulheres. Além disso, 30 alunos usam óculos e 15 deles são homens, o que indica que os outros 15 alunos com óculos são mulheres. Portanto, temos 25 homens sem óculos e 45 mulheres sem óculos.
Assim, a probabilidade de que seja mulher e não use óculos podemos encontrar mediante a regra: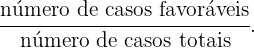
Neste caso o número de casos favoráveis é o número de mulheres que não usam óculos, ou seja, 45, enquanto que o número de casos totais é o total de alunos. Então,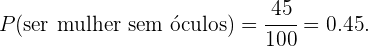
b) Se sabemos que o aluno selecionado não usa óculos, qual a probabilidade de que seja homem?
Seja  os eventos “ser homem” e “não usar óculos” respectivamente. Assim, a probabilidade que procuramos está dada por
os eventos “ser homem” e “não usar óculos” respectivamente. Assim, a probabilidade que procuramos está dada por 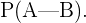
Sabemos então que 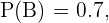 pois 70 dos cem alunos não usam óculos, isto é:
pois 70 dos cem alunos não usam óculos, isto é:
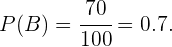
Por outro lado  é equivalente ao evento “ser homem e não usar óculos”, e de acordo com o exercício anterior, há 25 alunos que encontram-se dentro desta categoria, assim:
é equivalente ao evento “ser homem e não usar óculos”, e de acordo com o exercício anterior, há 25 alunos que encontram-se dentro desta categoria, assim: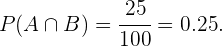
Seguindo com a definição de probabilidade condicional, sabemos que: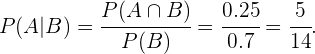
Uma viagem à Roma é sorteada entre os  melhores clientes de uma agência de automóveis.
melhores clientes de uma agência de automóveis.
Destes,  são mulheres,
são mulheres,  estão casados e
estão casados e  são mulheres casadas.
são mulheres casadas.
Pede-se:
- Qual será a probabilidade de que o premiado seja um homem solteiro?
- Se sabemos que o (a) premiado (a) é casado (a), qual a probabilidade de que seja uma mulher?
a) Qual será a probabilidade de que o premiado seja um homem solteiro?
Começamos notando que dentro da população temos 65 mulheres e 55 homens, pois a soma de indivíduos deve ser 120. Continuando com o mesmo raciocínio, sabemos que há 80 pessoas casadas e que 45 delas são mulheres, o que nos deixa com 35 homens casados e 20 solteiros.
Portanto, a probabilidade de que um homem solteiro seja premiado é de: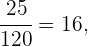
onde simplesmente aplicamos a regra: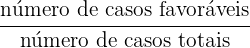
e identificando os casos favoráveis como os dos homens solteiros e os casos totais como o número total de indivíduos dos quais vão participar do sorteio.
b) Se sabemos que o (a) premiado (a) é casado (a), qual a probabilidade de que seja uma mulher?
No exercício anterior, calculamos o número de mulheres casadas que corresponde a 45. Sabendo que há 80 pessoas casadas, a probabilidade de que a viagem seja para uma mulher, levando em conta que o (a) premiado (a) é casado (a), é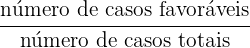
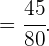
Neste caso o número de casos totais é o número de indivíduos casados, já que sabemos que o ganhador da viagem é uma pessoa casada. Enquanto que o número de casos favoráveis são as mulheres casadas.
Uma turma está composta de seis meninas e  meninos. Se formamos ao acaso um comitê de três, encontre a probabilidade de:
meninos. Se formamos ao acaso um comitê de três, encontre a probabilidade de:
- Selecionar três meninos
- Selecionar exatamente dois meninos e uma menina
- Selecionar pelo menos um menino
- Selecionar exatamente duas meninas e um menino
a) Selecionar três meninos
Podemos tratar este problema como se estivéssemos realizando duas extrações sem reposição.
Indicamos com  o evento de escolher um menino na extração
o evento de escolher um menino na extração  -ésima, com
-ésima, com 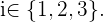 Com isso em mente e de acordo com a definição de probabilidade condicional:
Com isso em mente e de acordo com a definição de probabilidade condicional:
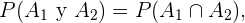
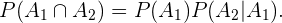
Para calcular 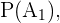 simplesmente dividimos o número de casos favoráveis entre o número de casos totais. Neste caso há 10 meninos possíveis de serem escolhidos, isto é, 10 é o número de casos favoráveis, e um total de 16 meninos, que representam o número de casos totais. Então,
simplesmente dividimos o número de casos favoráveis entre o número de casos totais. Neste caso há 10 meninos possíveis de serem escolhidos, isto é, 10 é o número de casos favoráveis, e um total de 16 meninos, que representam o número de casos totais. Então,
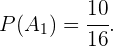
Por outro lado,
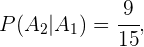
pois o número de casos favoráveis é 9, por já ter escolhido um menino. O total de meninos que restam para escolher é 15 agora.
Assim,
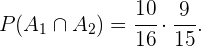
Aplicando esta premissa de maneira iterativa para a escolha do terceiro menino, teríamos que: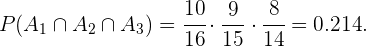
b) Selecionar exatamente dois meninos e uma menina
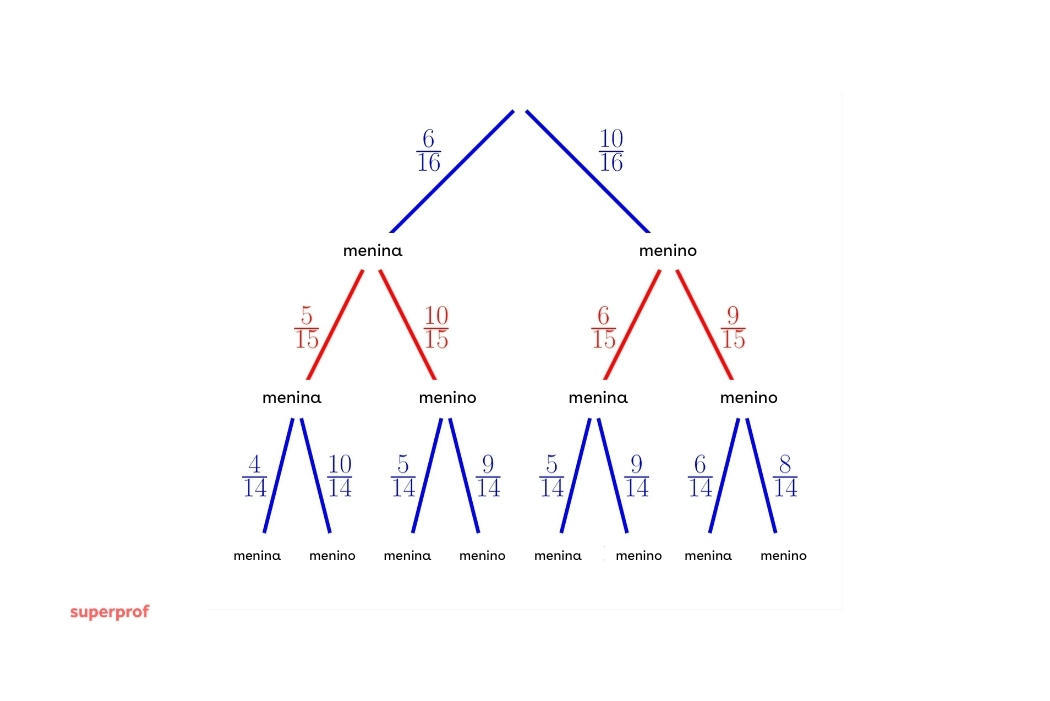
Para calcular esta probabilidade, primeiro necessitamos identificar os diferentes casos dos quais poderíamos selecionar dois meninos e uma menina. O primeiro caso é escolher 2 meninos e ao final uma menina. O segundo caso é escolher uma menina e ao final dois meninos. E, por último, um menino, uma menina e um menino. A probabilidade de cada caso podemos calcular fazendo a multiplicação da probabilidade em cada passo da figura apresentada no início.
Por exemplo, se no primeiro caso indicamos como evento  então,
então,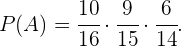
Logo, indicando como 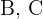 os eventos restantes, sabemos que:
os eventos restantes, sabemos que: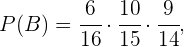
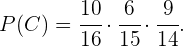
Por fim, a probabilidade que estamos procurando é a probabilidade de que qualquer destes eventos aconteça, ou seja 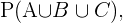 Como estes são eventos distantes, sabemos que:
Como estes são eventos distantes, sabemos que: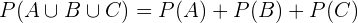
Portanto,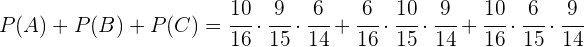
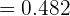
c) Selecionar pelo menos um menino
Para calcular a probabilidade de selecionar ao menos um menino, faremos,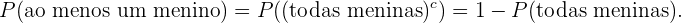
Podemos calcular a probabilidade de escolher três meninas de maneira completamente análoga ao inciso um deste exercício. Então,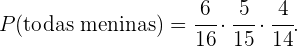
Logo,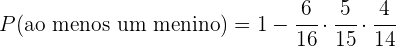
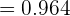
d) Selecionar exatamente duas meninas e um menino
Para calcular esta probabilidade, primeiro precisamos identificar os diferentes casos dos quais poderíamos selecionar duas meninas e um menino. O primeiro caso é escolher 2 meninas e ao final um menino. O segundo caso é escolher um menino e ao final duas meninas. E, por último, uma menina, um menino e uma menina. A probabilidade de cada caso podemos calcular fazendo a multiplicação da probabilidade em cada passo da figura apresentada no início.
Por exemplo, se o primeiro caso indicamos como evento  então,
então,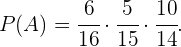
Logo, indicando como 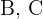 os eventos restantes, sabemos que,
os eventos restantes, sabemos que,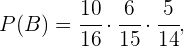
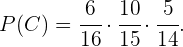
Por fim, a probabilidade que estamos procurando é a probabilidade de que qualquer destes eventos aconteça, ou seja 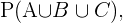 Como estes são eventos distantes, sabemos que:
Como estes são eventos distantes, sabemos que: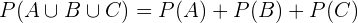
Portanto,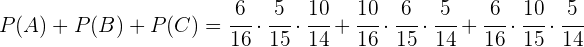
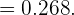
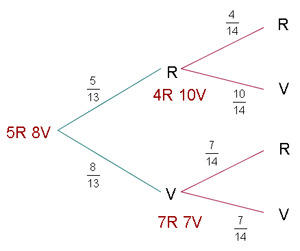
Uma urna contém  bolas roxas e
bolas roxas e  verdes.
verdes.
Extraímos uma bola e repomos com duas de outra cor.
Em seguida extraímos uma segunda bola
- A probabilidade de que a segunda bola seja verde
- A probabilidade de que duas bolas extraídas sejam da mesma cor
a) A probabilidade de que a segunda bola seja verde
Seja  o evento “a segunda bola é verde”, há duas possibilidades para tal evento, que a primeira bola seja roxa ou que seja verde. Representaremos isso como
o evento “a segunda bola é verde”, há duas possibilidades para tal evento, que a primeira bola seja roxa ou que seja verde. Representaremos isso como 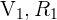 e é importante observar que estes casos são mutuamente excludentes, isto é, não podem ocorrer ao mesmo tempo. Portanto,
e é importante observar que estes casos são mutuamente excludentes, isto é, não podem ocorrer ao mesmo tempo. Portanto,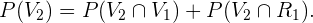
Seguindo a definição de probabilidade de uma interseção, sabemos que: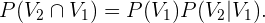
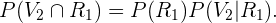
De acordo com o diagrama apresentado no início da solução,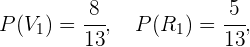
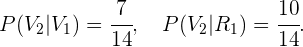
Com isso, obtemos: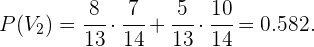
b) A probabilidade de que duas bolas extraídas sejam da mesma cor
Seja 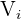 o evento “a bola i-ésima é verde” e
o evento “a bola i-ésima é verde” e  o evento “a bola i-ésima é roxa”, procuramos
o evento “a bola i-ésima é roxa”, procuramos 
Seguindo a definição de probabilidade de uma interseção, sabemos que,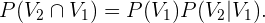
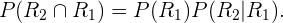
De acordo com o diagrama apresentado no início da solução,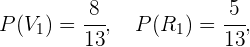
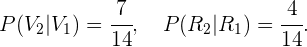
Com isso, obtemos: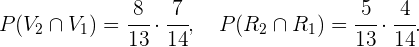
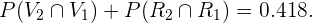
Supõe-se que  de cada
de cada  homens e
homens e  de cada
de cada  mulheres usam óculos.
mulheres usam óculos.
Se o número de mulheres é quatro vezes superior ao de homens, pede-se a probabilidade de nos depararmos:
- Com uma pessoa sem óculos
- Com uma mulher com óculos
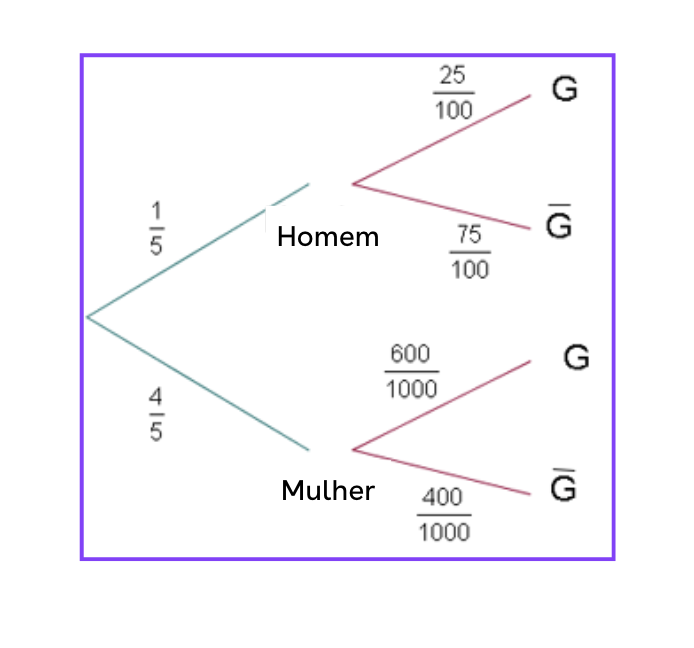
a) Com uma pessoa sem óculos
Do total da população, sabemos que  corresponde à proporção de mulheres e
corresponde à proporção de mulheres e  corresponde à proporção de homens. Desta maneira, cumpre-se a condição “o número de mulheres é quatro vezes superior à de homens”.
corresponde à proporção de homens. Desta maneira, cumpre-se a condição “o número de mulheres é quatro vezes superior à de homens”.
Logo, 25 de cada 100 homens usam óculos é equivalente à probabilidade de 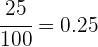 de encontrarmos um homem com óculos, onde sabemos que
de encontrarmos um homem com óculos, onde sabemos que  é a probabilidade de homens que não usam óculos. Com este mesmo raciocínio,
é a probabilidade de homens que não usam óculos. Com este mesmo raciocínio,  é a probabilidade de encontrarmos uma mulher com óculos, enquanto que
é a probabilidade de encontrarmos uma mulher com óculos, enquanto que  é a probabilidade de mulheres sem óculos. Em ambos os casos, apenas calculamos o quociente dos casos favoráveis entre os casos totais.
é a probabilidade de mulheres sem óculos. Em ambos os casos, apenas calculamos o quociente dos casos favoráveis entre os casos totais.
Seja  os eventos “não ter óculos”, “ser homem” e “ser mulher” respectivamente, estamos procurando
os eventos “não ter óculos”, “ser homem” e “ser mulher” respectivamente, estamos procurando 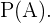 Como ser homem e ser mulher são eventos excludentes, sabemos que
Como ser homem e ser mulher são eventos excludentes, sabemos que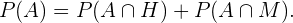
De acordo com as regras de probabilidade condicional,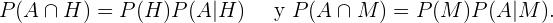
Como sabemos 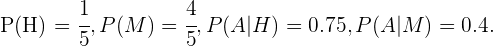
E substituindo estes valores na expressão anterior, obtemos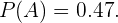
b) Com uma mulher com óculos
Do total da população, sabemos que  corresponde à proporção de mulheres e
corresponde à proporção de mulheres e  corresponde à proporção de homens. Desta maneira cumpre-se a condição “o número de mulheres é quatro vezes superior ao de homens”.
corresponde à proporção de homens. Desta maneira cumpre-se a condição “o número de mulheres é quatro vezes superior ao de homens”.
Observe que  é a probabilidade de encontrarmos uma mulher com óculos, enquanto que
é a probabilidade de encontrarmos uma mulher com óculos, enquanto que  é a probabilidade de mulheres sem óculos. Em ambos os casos, apenas calculamos o quociente de casos favoráveis entre os casos totais.
é a probabilidade de mulheres sem óculos. Em ambos os casos, apenas calculamos o quociente de casos favoráveis entre os casos totais.
Seja 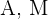 os eventos “ter óculos” e “ser mulher” respectivamente, estamos procurando
os eventos “ter óculos” e “ser mulher” respectivamente, estamos procurando 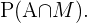
De acordo com as regras de probabilidade condicional,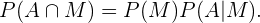
Como sabemos 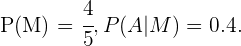 E substituindo estes valores na expressão anterior, obtemos
E substituindo estes valores na expressão anterior, obtemos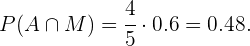
Em uma escola, os alunos podem optar em cursar como língua estrangeira o inglês ou o francês.
Em um determinado curso, 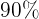 dos alunos estudam inglês e o resto francês.
dos alunos estudam inglês e o resto francês.
Os  dos que estudam inglês são meninos e dos que estudam francês
dos que estudam inglês são meninos e dos que estudam francês  são meninos.
são meninos.
Ao escolhermos um aluno ao acaso, qual é a probabilidade de ser menina?
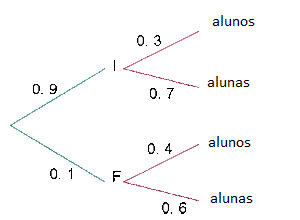
Vamos chamar de 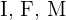 os eventos “estudar inglês”, “estudar francês”, “ser mulher”, respectivamente. Assim, procuramos a probabilidade de escolher uma mulher ao acaso, mas como todas as pessoas do centro escolar estudam inglês ou francês, a probabilidade solicitada pode ser calculada através das probabilidades seguintes
os eventos “estudar inglês”, “estudar francês”, “ser mulher”, respectivamente. Assim, procuramos a probabilidade de escolher uma mulher ao acaso, mas como todas as pessoas do centro escolar estudam inglês ou francês, a probabilidade solicitada pode ser calculada através das probabilidades seguintes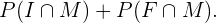
Para ambas probabilidades podemos fazer,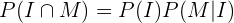
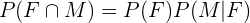
Desta maneira podemos utilizar a informação proporcionada, pois: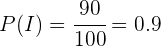
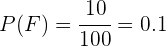
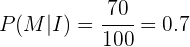
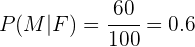
Substituindo todos estes valores, obtemos o seguinte cálculo,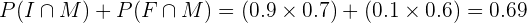
Uma caixa contém três moedas
Uma moeda é regular, a outra tem duas caras e uma outra está viciada, de modo que a probabilidade de obter cara é de 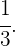 Selecionamos uma moeda ao acaso e lançamos ao ar.
Selecionamos uma moeda ao acaso e lançamos ao ar.
Encontre a probabilidade de que saia cara.
Seja  o evento “escolher a i-ésima moeda”, onde
o evento “escolher a i-ésima moeda”, onde 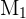 é a moeda regular,
é a moeda regular, 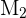 a moeda com duas caras e
a moeda com duas caras e  a moeda viciada. Neste contexto, se chamamos
a moeda viciada. Neste contexto, se chamamos  o evento “lançar a moeda e obter cara”, podemos calcular
o evento “lançar a moeda e obter cara”, podemos calcular  fazendo uma interseção com os eventos
fazendo uma interseção com os eventos 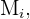 já que estes são mutuamente excludentes. Isto é,
já que estes são mutuamente excludentes. Isto é,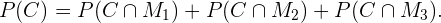
Com a definição de probabilidade condicional as seguintes igualdades são válidas.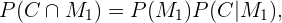
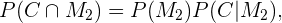
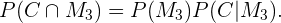
Como a escolha da moeda é feita ao acaso, sabemos que 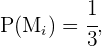 com
com  Logo,
Logo,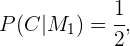
pois a primeira moeda é regular, o que quer dizer que têm uma cara e uma coroa, sendo assim, qualquer lado pode sair com a mesma probabilidade.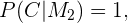
pois esta moeda tem duas caras, então não importa como caia, seu valor será cara.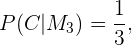
pois a última moeda está viciada de modo que a probabilidade de sair cara seja essa.
Assim,
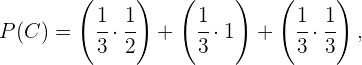
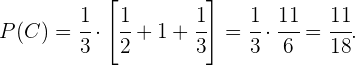
Resumir com IA:


