Duas equações com duas incógnitas formam um sistema quando o objetivo é encontrar sua solução comum.
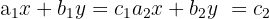
A solução de um sistema é um par de números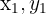 
, tais que, substituindo 
por 
e 
por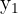 
, satisfazem simultaneamente as duas equações.
Sistemas equivalentes
Dois sistemas de equações são equivalentes quando possuem a mesma solução.
Critérios de equivalência
1 Se somamos ou subtraímos a mesma expressão a ambos os membros de uma equação de um sistema, o sistema resultante é equivalente.
2 Se multiplicamos ou dividimos ambos os membros das equações de um sistema por um número diferente de zero, o sistema resultante é equivalente.
3 Se, em uma equação de um sistema, somamos ou subtraímos outra equação do mesmo sistema, o sistema resultante é equivalente ao fornecido.
4 Se, em um sistema, substituímos uma equação por outra que resulte da soma das duas equações do sistema previamente multiplicadas ou divididas por números não nulos, obtemos outro sistema equivalente ao primeiro.
5 Se, em um sistema, alteramos a ordem das equações ou a ordem das incógnitas, obtemos outro sistema equivalente.
Resolução de sistemas de equações
Existem vários métodos para resolver sistemas de equações. Neste texto, apresentaremos três dos mais utilizados.
Método de substituição
1 Isola-se uma incógnita em uma das equações.
2 Sustitui-se a expressão na outra equação, obtendo-se uma equação com uma incógnita.
3 Resolve-se a equação.
4 O valor obtido é substituído em qualquer das duas expressões em que aparecia a incógnita isolada.
5 Os dois valores obtidos constituem a solução do sistema.
Método de comparação
1 Isola-se a mesma incógnita em ambas as equações.
2 Igualam-se as expressões, obtendo-se uma equação com uma incógnita.
3 Resolve-se a equação.
4 O valor obtido é substituído em qualquer das duas expressões em que aparecia a incógnita isolada.
5 Os dois valores obtidos constituem a solução do sistema.
Método da adição (ou redução)
1 Preparam-se as duas equações, multiplicando-as pelos números que sejam convenientes.
2 Somam-se ou subtraem-se as equações, de modo que desapareça uma das incógnitas.
3 Resolve-se a equação resultante.
4 O valor obtido é substituído em uma das equações iniciais e resolve-se.
5 Os dois valores obtidos constituem a solução do sistema.
Tipos de sistemas
Sistema possível e determinado
Possui uma única solução.
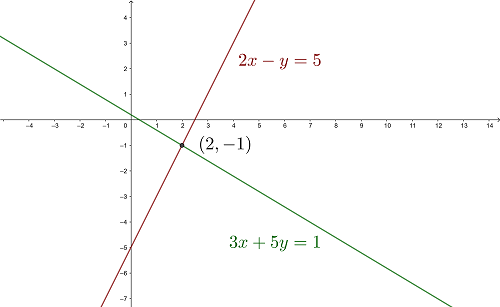
Graficamente, a solução é o ponto de interseção das duas retas.
Exemplo: Determine as soluções do sistema:
Aplicamos o método da adição, para o qual multiplicamos por cinco ambos os membros da segunda equação e obtemos o sistema equivalente:
Somamos as equações e resolvemos a equação resultante:
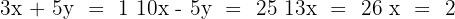
Substituímos o valor obtido na segunda equação:
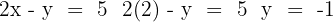
A solução é 
, portanto o sistema é possível e determinado.
Sistema possível e indeterminado
O sistema possui infinitas soluções.
Graficamente, obtemos duas retas coincidentes. Qualquer ponto da reta é solução.
Exemplo: Determine as soluções do sistema:
Aplicamos o método da adição, para o qual multiplicamos por três ambos os membros da segunda equação e obtemos o sistema equivalente:
As retas são coincidentes, logo existem infinitas soluções. Assim, trata-se de um sistema possível e indeterminado.
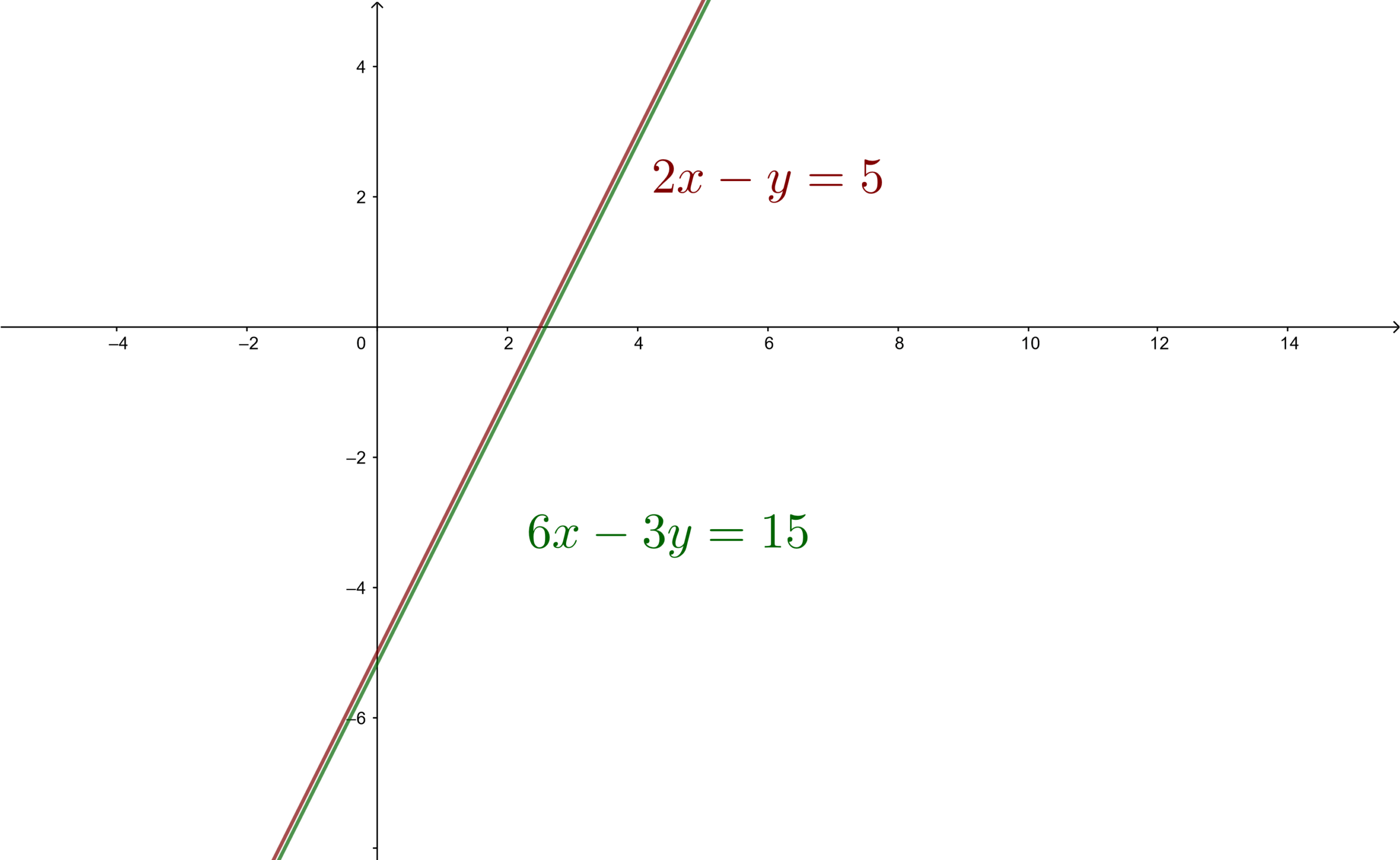
Sistema impossível
Não tem solução
Graficamente obtemos duas retas paralelas.
Exemplo: Determine as soluções do sistema:
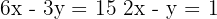
Aplicamos o método da adição, para o qual multiplicamos por três ambos os membros da segunda equação e obtemos o sistema equivalente:
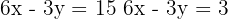
As retas não são coincidentes, mas possuem a mesma inclinação 
logo são paralelas e não existe solução. Assim, trata-se de um sistema impossível.
Gostou desse artigo? Deixe uma nota!
Loading...
aula boa eu tire 10 na prova
🙌