Temas
- Termo geral de uma progressão geométrica
- Interpolação de n termos em uma progressão geométrica
- Soma de n termos consecutivos de uma progressão geométrica
- Soma dos termos de uma progressão geométrica decrescente
- Produto de dois termos equidistantes
- Produto de n termos consecutivos de uma progressão geométrica
As progressões geométricas têm diversas aplicações no dia a dia, que nos permite fazer o cálculo de juros em empréstimos, nos ajuda na compra de produtos, além de serem úteis para medir o crescimento populacional de uma espécie. Vamos te apresentar um pouco sobre suas propriedades.
Uma progressão geométrica é uma sequência na qual cada termo é obtido multiplicando o anterior por uma quantidade fixa r, chamada razão.
Exemplo:
Se você tem um primeiro termo a1=3 e uma razão r=4 "você pode construir a próxima progressão geométrica:
3, 12, 48, 192, ...
Já que ao operar o primeiro termo a1=3 com a razão r=4 obtém-se que:
3
3(4)=12
12(4)=48
48(4)=192, ...
Como é possível observar, o 12 é obtido multiplicando 3 por 4, que é a razão, e assim sucessivamente até chegar ao termo desejado n.
Por outro lado, se conhecemos dois termos consecutivos an e an+1 da progressão geométrica, mas não é conhecida a razão r, a razão r pode ser calculada dividindo esses termos, conforme indicado na seguinte equação:
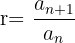
Exemplo:
Dada a seguinte progressão geométrica: 3, 6, 12, 24, 48, … observa que quaisquer dos dois termos consecutivos tem a razão r=2, já que, quando aplicada à equação anterior, vamos obter que:
r=6/3=2
r=12/6=2
r=24/12=2
r=48/24=2

Termo geral de uma progressão geométrica
O termo geral de uma sequência é a expressão an que permite conhecer qualquer termo em função de sua posição n.
Ao desejar conhecer o valor do termo geral an, você terá duas situacões:
1 Descobrir o primeiro termo a1 e a razão r . Neste caso, é possível conhecer qualquer outro termo da progressão com o uso da seguinte fórmula:
an = a1 · rn-1
Exemplo:
Você tem a seguinte progressão e precisa calcular o valor do termo na posição 20.
3, 6, 12, 24, 48, …
Identificar que a1=3, a razão r =2 e como você precisa calcular o valor do termo na posição 20, assim, n=20; ao substituir os valores na fórmula, obtém-se que:
a20 = 3· 220-1 = 3· 219 = 1, 572, 864
Desta forma, o valor do termo 20 é 1, 572, 864.
2 Quando não se conhece o primeiro termo a1 da progressão geométrica, mas se conhece qualquer outro termo ak e a razão r. Nesse caso, é possível calcular o valor de qualquer termo na posição desejada an usando a seguinte fórmula:
an = ak · rn-k
Onde k é o número da posição do termo que você conhece e n é a posição do termo que você deseja conhecer.
Exemplo:
Vamos supor que ak é igual a 24, onde k=4 e a razão r=2, ao substituir os valores na fórmula temos que:
an = a4 · 2n-4</strong
Agora, se quer conhecer o valor de a1, é calculado da seguinte maneira:
a1 = 24· 21-4= (24)· 2-3 = (24)(1/8) =3
Agora, no caso de querer conhecer o valor de a10 é calculado da mesma maneira que o exemplo anterior:
a10 = 24· 210-4= (24)· 26 = 1536
Não se esqueça que n é a posição do termo que você deseja conhecer.
Como você perceberá, não importa qual termo an que você quer conhecer, basta calcular com a fórmula apropriada, de acordo com a situação. Seja conhecendo o primeiro termo a1 ou qualquer outro ak da progressão geométrica, juntamente com a razão r.
Interpolação de n termos em uma progressão geométrica
Interpolar médias geométricas ou proporcionais entre dois números a e b, é construir uma progressão geométrica que tenha como extremos os elementos a e b, e a uma quantidade determinada de valores intermediários. Para conseguir isso, é necessário saber quantos elementos m você quer interpolar e, com essa informação, calcular a razão r adequada. Já com r e o valor de a, é possível construir a progressão geométrica.
A fórmula para conhecer a razão r adequada para interpolar m médias geométricas entre a e b é a seguinte:
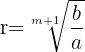
Exemplo:
Interpolar 3 médias geométricas entre a=-2 e b=-4802. Primeiro, encontramos a razão r adequada.
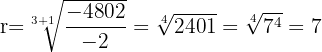
Já que conhecemos que r=7, vamos usar para construir a progressão geométrica, tomando como primeiro valor o a=-2 e vai-se multiplicando pela razão r=7 sucessivamente e vamos obter:
-2, -14, -98, -686, -4802.
Observe que foram interpolados 3 números entre -2 e -4802, formando a progressão.
Exemplo:
Interpolar três médias geométricas entre a=3 e b=48. Primeiro, encontramos a razão r adequada.
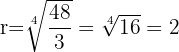
Observe que a razão encontrada é usada para construir a progressão geométrica, obtendo:
3, 6, 12, 24 , 48.
Do mesmo modo que o exemplo anterior, 3 números foram interpolados, mas agora entre 3 e 48, formando a progressão desejada.
Em conclusão, a quantidade de termos a ser interpolada m para que seja necessária ou desejada, entre a e b, é apenas uma questão de calcular a razão r adequada fazendo uso da fórmula.
Soma de n termos consecutivos de uma progressão geométrica
Para conseguir somar n termos consecutivos de uma progressão geométrica, a primeira coisa que devemos fazer é conhecer a razão r, ao primeiro termo a1 , e ao número de valores n que deseja fazer a soma da sequência.
Uma vez que esses dados são conhecidos, é feito uso da fórmula:
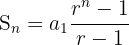
em que Sn é a soma de n termos consecutivos de uma progressão geométrica.
Exemplo:
Calcule a soma dos primeiros 5 termos da seguinte progressão: 3, 6, 12, 24, 48, …
É calculada a razão r, dividindo dois valores consecutivos, como foi visto inicialmente
r=6/3 =2
agora com r=2, n=5 e a1 =3 os valores são substituídos na fórmula, resultando em:
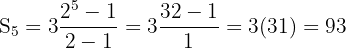
e com isso é conhecido o resultado de somar n aos termos solicitados, tendo como resultado:
3 + 6 + 12 + 24 + 48 = 93
Observe que uma vantagem de realizar a adição de n termos com essa operação é que economiza muito trabalho, ao contrário de fazer a soma diretamente, pois há a possibilidade de que a quantidade de termos n a ser somada seja muito grande.
Soma dos termos de uma progressão geométrica decrescente
Há ocasiões em que é necessário somar todos os termos de uma progressão geométrica decrescente ilimitada. Para que a soma faça sentido, é necessário que o valor da razão esteja compreendido entre -1 e 1; caso contrário, a soma não seria possível, pois não teria um resultado numérico.
A fórmula que auxilia a determinar o resultado da soma de todos os termos
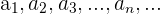
com -1 < r < 1 é:
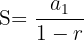
Com essa fórmula é possível calcular a soma de todos os termos da progressão, ou seja:

Exemplo:
Para calcular a soma dos termos da progressão geométrica decrescente ilimitada, formada por a1=2 e r=0.5.
Vamos lembrar que é necessário ter o valor de r entre -1 y 1, e, neste caso r=0.5 , atendendo a condição, significa que podemos continuar com o processo.
Agora vamos construir a progressão:
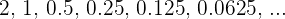
e assim sucessivamente (as reticências indicam que o processo continua sem terminar).
Então, com isso, conhecemos o resultado da soma de todos os termos, substituindo na fórmula:
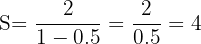
significa que
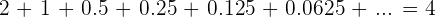
Obtendo, desta maneira, o resultado buscado.
A soma que estamos calculando agora difere da anterior, pois aqui estamos somando uma quantidade ilimitada de termos (anteriormente a soma era de uma quantidade finita de termos). Por esse motivo, foi necessário utilizar a fórmula mencionada.
Produto de dois termos equidistantes
Quando se possui uma progressão geométrica, na qual a1 é o primeiro termo e an é o último, é possível entender que dois valores são equidistantes se estiverem a mesma distância tanto de um extremo quanto do outro da progressão, respectivamente, por exemplo:
a2 está equidistante de an-1
a3 está equidistante de an-2
a4 está equidistante de an-3
e, assim, sucessivamente.
Uma propriedade indica que a multiplicação entre dois valores equidistantes é igual ao produto dos extremos dessa progressão, ou seja:
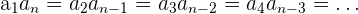
Exemplo:
Se temos a seguinte progressão geométrica:
5, 10, 20, 40, 80, 160
Podemos observar que o produto dos extremos
5 (160) = 800
é igual ao produto de quaisquer dois termos equidistantes, por exemplo:
10 (80) = 800
20 (40) = 800
Esta propriedade tem a vantagem de multiplicar apenas os extremos, permitindo assim que se conheça o resultado da multiplicação de qualquer par de termos equidistantes, e também pode ser útil para resultados futuros.
Produto de n termos consecutivos de uma progressão geométrica
Se deseja multiplicar uma quantidade n de termos consecutivos de uma progressão geométrica, é suficiente conhecer os valores dos extremos a1 e an , ou seja, para conhecer o produto dos termos
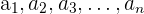
É necessário usar a fórmula:
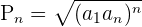
Em outras palavras, a fórmula permite saber de maneira efetiva o resultado do produto seguinte:
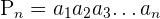
Exemplo:
Calcule o produto dos 5 primeiros termos da progressão
3, 6, 12, 24, 48, …
Aqui podemos ver que a1 =3 a5 =48 com n=5 assim, a substituição ficará:
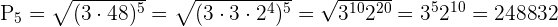
Em outras palavras, o resultado obtido é o seguinte:
(3) (6) (12) (24) (48) = 248, 832
E assim como na soma de n termos consecutivos, aqui também é mais conveniente e prático conhecer o resultado do produto com o uso da fórmula, pois pode-se ter uma grande quantidade de fatores.
Resumir com IA:












