Temas
Problemas de áreas e perímetros
Qual é a área de um retângulo sabendo que seu perímetro é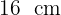 
e que sua base é o triplo de sua altura?
1 Estabelecemos as variáveis
base do retângulo
altura do retângulo
2 Escrevemos as equações
perímetro
3Formamos o sistema, na primeira equação estabelecemos a relação entre a base e a altura e, na segunda, o perímetro.
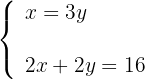
4Substituímos o valor de 
da primeira equação na segunda equação, de modo que calculamos o valor de 
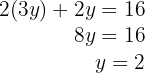
5Para encontrar o valor de substituímos na primeira equação.
6Assim, a base mede 
e a altura é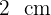 
Qual é o perímetro de um retângulo sabendo que sua área é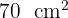 
e que sua base é três centímetros maior que sua altura?
1 Estabelecemos as variáveis
base do retângulo
altura do retângulo
2 Escrevemos as equações
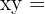área
3Formamos o sistema, na primeira equação estabelecemos a relação entre a base e a altura e, na segunda, a área.
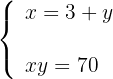
4Substituimos o valor de da primera equação na segunda equação, de modo que calculamos o valor de
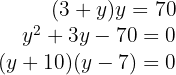
Logo, 
5Para encontrar o valor de substitimos na primeira equação.
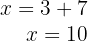
6Assim, a base mede 
e a altura é 
e o perímetro é de 
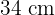
A base de um triângulo é três unidades maior que sua altura. Se sua área é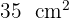 
, quais são as medidas do triângulo?
1 Estabelecemos as variáveis
base do triângulo
altura do triângulo
2 Escrevemos as equações:
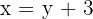
3Formamos o sistema, na primeira equação estabelecemos a relação entre a base e a altura e na segunda, a área.
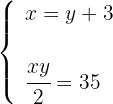
4Substituimos o valor de da primeira equação na segunda equação, de modo que calculamos o valor de
Logo, o valor é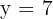 
, (o valor 
é desconsiderado, pois não se pode ter medidas negativas).
5Para encontrar o valor de substituimos na primeira equação.
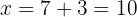
6Assim, a base mede e a altura é
A base de um triângulo é o dobro de sua altura. Se sua área é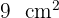 
, quais são as medidas do triângulo?
1 Estabelecemos as variáveis
base do triângulo
altura do triângulo
2 Escrevemos as equações.
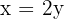
3Formamos o sistema e na primeira equação estabelecemos a relação entre a base e a altura e na segunda, a área.
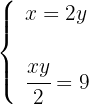
4Substituimos o valor de da primeira equação na segunda equação, de modo que calculamos o valor de
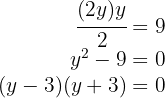
Logo, o valor é 
, (o valor 
não é considerado, pois não se pode ter medidas negativas).
5Para encontrar o valor de substituimos na primeira equação.
6Assim, a base mede e a altura é de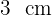 
A base de um triângulo isósceles é 2 unidades maior que sua altura. Se sua área é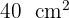 
, quais são as medidas do triângulo?
1 Estabelecemos as variáveis
base do triângulo
altura do triângulo
2 Escrevemos as equações.
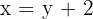
3Formamos o sistema e na primeira equação estabelecemos a relação entre a base e a altura e na segunda, a área.
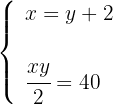
4Substituimos o valor de da primeira equação na segunda equação, de modo que calculamos o valor de
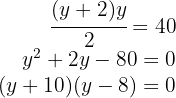
Logo, o valor é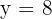 
, (o valor é desconsiderado, pois não se pode ter medidas negativas).
5Para encontrar o valor de substituimos na primeira equação.
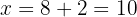
6Assim, a base mede e a altura é de 
Problemas da fazenda
Uma fazenda tem perus e porcos. No total há 
cabeças e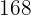 
patas. Quantos porcos e perus há?
1 Estabelecemos as variáveis
número de perus
número de porcos
2 Escrevemos as equações, na primeira equação relacionamos as cabeças e na segunda equação as patas:
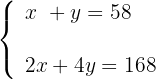
3Resolvemos o sistema por redução, multiplicando a primeira equação por -2:
4Para encontrar o valor de substituímos o valor de na primeira equação:
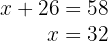
5Assim, há 
perus e 
porcos.
Pedro e João têm perus. João diz: se você me der 
perus, teremos a mesma quantidade. Pedro responde: se você me der perus, eu teria três vezes mais do que você teria. Quantos perus tem cada um?
1 Estabelecemos as variáveis
número de perus de Pedro
número de perus de João
2 Escrevemos as equações:
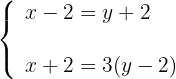
3Isolamos na primeira equação e substituímos na segunda:
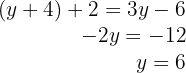
4Para encontrar o valor de substituímos o valor de na primeira equação:
5Assim, Pedro tem 
perus e João tem 
perus.
Maria vai ao mercado e compra 
maçãs e laranjas por R$ 
.Se tivesse comprado maçãs e laranjas, ela teria pago R$ 
. Qual é o preço de cada fruta?
1 Estabelecemos as variáveis
preço da maçã
preço da laranja
2Formamos o sistema:
3Resolvemos o sistema por redução, multiplicando a primeira equação por -2 e a segunda por 3:
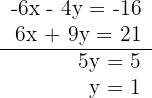
4Calculamos o valor de substituindo o valor de na primeira equação:
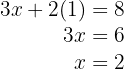
5 Assim,o preço da maçã é R$ e o da laranja é R$ 
.
Pedro compra 
peras e mangas por R$ 
. No dia seguinte, compra pera e mangas e paga R$
. Se em ambos os dias o preço das frutas não apresentou aumento nem diminuição, qual é o preço de cada fruta?
1 Estabelecemos as variáveis
preço da pera
preço da manga
2Formamos o sistema:
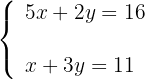
3Resolvemos o sistema por redução, multiplicando a segunda equação por -5:
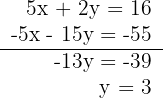
4Calculamos o valor de substituindo o valor de na segunda equação:
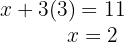
5 Assim, o preço da pera é R$ e o da manga é R$ .
No mercado, vendem 
maçãs e pêssegos por R$ . Também vendem maçã e pêssegos por R$ . Qual é o preço de cada fruta?
1 Estabelecemos as variáveis
preço da maçã
preço do pêssego
2Formamos o sistema:
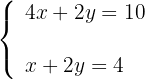
3Resolvemos sistema por redução:
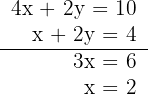
4Calculamos o valor de substituindo o valor de na primeira equação:
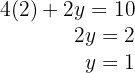
5 Assim, o preço da maçã é R$ e o do pêssego é R$ .
Problemas aritméticos
A soma de dois números é 11 e sua diferença é 7, quais são esses números?
1 Estabelecemos as variáveis
número maior
número menor
2Formamos o sistema:
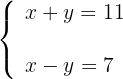
3Resolvemos o sistema por redução:
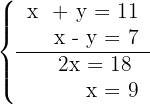
4Substituimos o valor de na primeira equação:
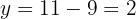
5Assim, os números procurados são 
e .
A soma de dois números é 33 e a terceira parte do maior menos a metade do menor é 1, quais são esses números?
1 Estabelecemos as variáveis
número maior
número menor
2Formamos o sistema:
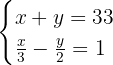
3Resolvemos o sistema por redução, multiplicando a segunda equação por 2:
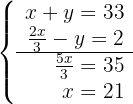
4Substituímos o valor de na primeira equação:
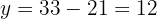
5Assim, os números procurados são 
e 
.
A soma de dois números é 21 e um deles é igual ao dobro do outro, quais são esses números?
1 Estabelecemos as variáveis
número maior
número menor
2Formamos o sistema:
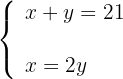
3Resolvemos o sistema por substituição:
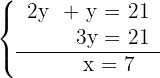
4Substituimos o valor de na segunda equação:
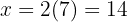
5Assim, os números procurados são 
e .
A cifra das dezenas de um número de duas cifras é o dobro da cifra das unidades, e se a esse número subtrairmos 
, obtemos o número que resulta ao inverter a ordem das suas cifras. Qual é esse número?
1 Estabelecemos as variáveis:
cifra das unidades
cifra das dezenas
2 Representamos o número:
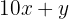
3 Representamos o número invertido:
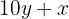
4Formamos o sistema:
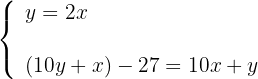
5Substituimos o valor de na segunda equação:
6Resolvemos a equação:
7Calculamos o valor de
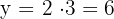
8O número procurado é 
Encontre um número de duas cifras sabendo que sua cifra das dezenas soma com a cifra das unidades e que, se invertermos a ordem das suas cifras, obtemos um número que é igual ao primeiro menos .
1 Estaabelecemos as variáveis
cifra das unidades
cifra das dezenas
2 Escrevemos as condições:
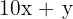número
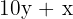número invertido
3Formamos o sistema:
4Isolamos na primeira equação e na segunda fazemos a operação:
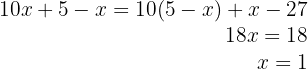
5Substituimos o valor de na primeira equação:
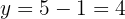
6Assim, o número é 
Problemas de custos
João comprou um computador e uma televisão por R$ 
e os vendeu por R$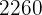 
. Quanto custou cada ítem, sabendo que na venda do computador ele obteve um lucro de 
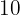e na venda da televisão ele obteve um lucro de 
?
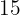1 Estabelecemos as variáveis
preço do computador
preço da televisão
2 Escrevemos os preços de venda:
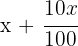
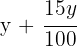
3Formamos um sistema com a equação de compra e outra com a equação da venda:
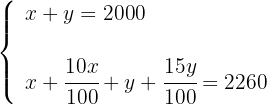
4Eliminamos os denominadores:
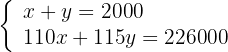
5Resolvemos o sistema por redução, multiplicando a primeira equação por -110:
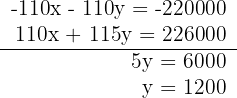
6Substituimos o valor de na primeira equação:
Assim, o preço do computador é R$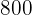 
e o preço da televisão é R$ 
.
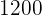Antonio diz a Pedro: "O dinheiro que tenho é o dobro do que você tem", e Pedro responde: "Se você me der seis reais, teremos a mesma quantidade". Quanto dinheiro tinha cada um?
1 Estabelecemos as variáveis
quantia de dinheiro de Antônio
quantia de dinheiro de Pedro
2Formamos o sistema, na primeira equação expressamos o que diz Antônio e na segunda expressamos o comentário de Pedro, lembrando que se ele der R$ , terá R$ a menos:
3Resolvemos o sistema por substituição, substituímos o valor de na segunda equação:
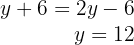
4Calculamos o valor de na primeira equação:
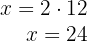
5Assim, Antônio tem R$ 
reais e Pedro tem R$ reais.
Em uma empresa trabalham 
pessoas. 
dos homens e 
das mulheres usam óculos. Se o número total de pessoas que usam óculos é igual a , quantos homens e quantas mulheres há na empresa?
1 Estabelecemos as variáveis
número de homens
número de mulheres
2 Escrevemos as condições para homens e mulheres que usam óculos:
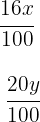
3Formamos o sistema:
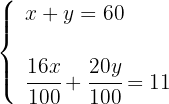
4Eliminamos os denominadores na segunda equação:
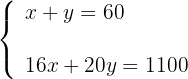
5Resolvemos na segunda equação, isolando da primeira equação.
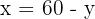
6Substituimos na segunda equação e resolvemos:
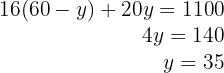
7Substituimos o valor de na primeira equação:
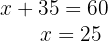
8Assim, o número de homens é 
e o de mulheres é 
.
Pagamos R$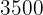 
na compra de dois eletrodomésticos. Se no primeiro tivéssemos recebido um desconto de 
e no segundo um desconto de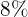 
, teríamos pago R$ 
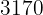. Qual é o preço de cada eletrodoméstico?
1 Estabelecemos as variáveis
preço do primeiro
preço do segundo
2 Escrevemos as condições dos descontos:
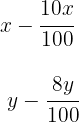
3Formamos o sistema:
4Eliminamos os denominadores na segunda equação:
5Resolvemoso sistema por redução, multiplicando a primeira equação por -90:
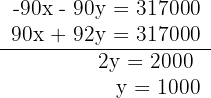
6Calculamos o valor de substituindo o valor de na primeira equação:
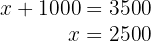
7 Assim, o preço do primeiro eletrodoméstico é de R$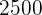 
e o do segundo eletrodoméstico é R$ 
.
Na compra de dois cadernos e três lápis foi pago R$ e pela compra de um caderno e quatro lápis foi pago R$ . Qual é o custo de cada ítem?
1 Estabelecemos as variáveis
preço do caderno
preço do lápis
2Formamos o sistema:
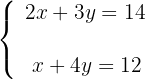
3Resolvemos o sistema por redução, multiplicando a segunda equação por -2:
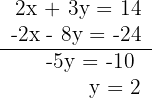
4Calculamos o valor de substituindo o valor de na segunda equação:
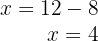
5 Assim, o preço do caderno é R$ e o lápis é R$ .
Gostou desse artigo? Deixe uma nota!
Loading...
aula boa eu tire 10 na prova
🙌