Temas
Bem vindos à nossa página dedicada a problemas de permutação, variação e combinação! Fizemos esta página para te proporcionar um aprendizado dinâmico e eficiente no estudo desta importante rama da probabilidade.
Lembre-se de que uma permutação é uma disposição ordenada de objetos de um conjunto cuja ordem importa. Utilizamos ela quando selecionamos todos os elementos de um conjunto para formar uma sequência.
Uma variação é similar a uma permutação, mas neste caso não utilizamos todos os elementos do conjunto. Ela refere-se a uma disposição ordenada de r elementos tirados de um conjunto de n elementos, onde a ordem continua sendo importante.
Uma combinação é uma seleção não ordenada de elementos tirados de um conjunto cuja ordem não importa. Utilizamos ela quando escolhemos elementos de um conjunto sem se preocupar com a ordem em que foi feita.
A seguir vamos apresentar uma grande variedade de exercícios com soluções sobre estes três importantes conceitos. Confira e aperfeiçoe suas habilidades!
Permutação
De quantas maneiras diferentes podem se sentar oito pessoas em uma fileira de assentos?
Sim, entram todos os elementos. Consideramos que as 
pessoas sentam na fileira.
Sim, importa a ordem. Se são organizados de maneira diferente, isso contaria como uma outra forma.
Não. Os elementos não se repetem. Uma pessoa não pode ser repetida.
Pelas características, trata-se de uma permutação.
Quantos números de 
dígitos diferentes podem ser formados com os dígitos: 
?
Observe que na pergunta são mencionados dígitos diferentes.
Não entram todos os elementos. De 
dígitos entram apenas
Sim, importa a ordem. São números diferentes o 
Não. Os elementos não se repetem. O enunciado pede que as dígitos sejam diferentes
Pelas características, trata-se de uma variação.
De quantas formas diferentes podem sentar oito pessoas ao redor de uma mesa redonda?
Neste caso nos interessa calcular de quantas formas podem ser acomodadas pessoas de forma circular. Desse modo, devemos recorrer às permutações circulares
Quantos bilhetes de aposta de um jogo de futebol devemos preencher para conseguir acertar os 
resultados?
Em cada uma das partidas podemos apostar que a equipe local ganhe, empate ou perca. Desse modo
m < n
Sim, entram todos os elementos. Neste caso o número de ordem é maior que o número de elementos
Sim, importa a ordem.
Sim, os elementos se repetem.
Pelas características, trata-se de uma variação.
Com as dígitos 
e , quantos números de cinco dígitos podemos formar? Quantos são pares?
a) Números de dígitos.
Sim, entram todos os elementos: 
b) Números de dígitos pares
Se o número é par, ele pode apenas terminar em 
.
Quantos números de nove dígitos podemos formar com os números
Sim, entram todos os elementos.
Sim, importa a ordem.
Sim, os elementos se repetem.
Pelas características, trata-se de uma permutação com repetição
Quantas ordens diferentes podemos fazer com as letras da palavra livro que comecem pela vogal?
A palavra começa com i ou o seguida de 
letras restantes, tiradas de em .
Sim, entram todos os elementos.
Sim, importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma permutação
Para a primeira letra há 
maneiras de fazer e para o restante há 
, já que trata-se de ordenar as letras l, b, r, e a que não usamos no início. Então as formas totais é igual a
Quantos números de cinco dígitos diferentes podemos formar com números ímpares? Quantos deles são maiores que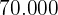 
?
a) Números de cinco dígitos diferentes
Os números ímpares:
Sim, entram todos os elementos.
Sim, importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma permutação
b) Maiores que 
Se é ímpar, ele pode começar apenas por 7 ou 8
Em um mastro de um barco podemos hastear três bandeiras vermelhas, duas azuis e quatro verdes. Quantos sinais diferentes podem ser indicados ao colocarmos as nove bandeiras?
Sim, entram todos os elementos.
Sim, importa a ordem.
Sim, os elementos se repetem.
Pelas características, trata-se de uma permutação com repetição
Uma mesa presidencial está formada por oito pessoas. De quantas maneiras diferentes elas podem se sentar se o presidente e o secretário vão sempre juntos?
a) É preciso considerar quantas maneiras existem de ocupar o espaço para o presidente e o secretário. Este espaço para duas pessoas pode ser a partir do primeiro lugar, do segundo, do terceiro, até o sétimo, no qual o presidente e o secretário ocupam os últimos dois lugares. No total há 
formas de escolher este espaço.
São formados dois grupos, o primeiro de pessoas (presidente e secretário) e o segundo com 
pessoas. Os dois grupos cumprem:
Sim, entram todos os elementos.
Sim, importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma permutação.
Ordenamos em uma fileira bolas vermelhas, bolas brancas e bolas azuis. Se as bolas com a mesma cor não se distinguem entre si, de quantas formas possíveis elas podem ser ordenadas?
Sim, entram todos os elementos.
Sim, importa a ordem.
Sim, os elementos se repetem.
Pelas características, trata-se de uma permutação com repetição.
Quatro diferentes livros de matemática, seis diferentes de física e dois diferentes de química são colocados em uma estante. De quantas formas distintas é possível ordená-los se:
- Os livros de cada matéria devem estar todos juntos.
- Somente os livros de matemática devem estar juntos.
a) Os livros de cada matéria devem estar todos juntos.
Ordem das matérias
Primeiro temos que escolher a ordem que teriam as matérias. Por exemplo: primeiro os livros de matemática, depois os de química e finalmente os de física. São 3 matérias, onde:
Sim, entram todos os elementos.
Sim, importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma permutação.
Existem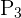 
de escolher como organizar as matérias.
Ordem dos livros por seção
Já que foi escolhido esse modo, vamos calcular as diferentes formas de colocar os livros de cada matéria no espaço que lhe corresponde.
Novamente:
Sim, entram todos os elementos.
Sim, importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma permutação.
Existem formas de colocar os livros de matemática no espaço que lhe corresponde, 
formas de colocar os livros de física e formas de colocar os livros de química.
Finalmente, o total de formas de colocar são:
b) Somente os livros de matemática devem estar juntos.
Ordem da seção de matemática
Primeiro tenho que considerar quantas maneiras há de organizar o espaço para os livros de matemática na estante.
O espaço para os livros de matemática podem começar do primeiro espaço, do segundo, do terceiro… até o nono, pois deste modo os livros de matemática ficariam no final, como é mostrado a seguir:
Então, no total, existem 
formas para escolher a posição na qual irão os livros de matemática.
Ordem dos livros do espaço designado
Com a seção já escolhida, existem maneiras de colocar os livros de matemática nesse espaço.
Sobram 8 espaços vazios para colocar o resto dos livros, sem nenhuma restrição, onde:
Sim, entram todos os elementos.
Sim, importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma permutação. Existem 
maneiras de colocar o resto dos livros.
No total, as maneiras de colocar os livros na estante em que os livros de matemática estejam juntos são:
Quantas maneiras diferentes de acertar uma bola são possíveis para uma equipe de baseball com jogadores?
Como cada jogador de baseball pode ter uma rodada para rebater, então, sim, importa a ordem e não são permitidas repetições. Desse modo, trata-se de uma permutação. Assim, existem:
maneiras possíveis de rebater.
Uma aula de matemática está composta de mulheres e homens. O professor desta disciplina decide fazer uma prova na qual todos os estudantes serão classificados de acordo com seu desempenho na prova. Se levamos em conta que dois estudante não obtenham a mesma classificação:
- Quantas classificações diferentes são possíveis?
- Se as mulheres são classificadas entre elas mesmas e os homens entre eles mesmos, quantas classificações diferentes são possíveis?
a) Dado que cada ranking corresponde a uma organização particular de 
pessoas, na qual, sim, importa a ordem, e não são permitidas repetições, então a resposta dessa parte é:
.
b) Agora consideramos as mulheres e os homens separadamente. Dado que existem 
classificações possíveis para as mulheres e 
classificações possíveis para os homens, então existem
classificaçõs possíveis neste caso.
Um torneio de xadrez tem como participantes competidores dos quais são dos Estados Unidos, são da Rússia, são da Índia e 
é da Espanha. Se ao final do torneio a organização mostra apenas as nacionalidades dos jogadores na posição na qual finalizaram o torneio, então quantos rankings são possíveis?
Como sabemos, se enumeramos os jogadores de 
, então teríamos um total de 
rankings diferentes possíveis. Agora, como é relevante apenas a nacionalidade e não o competidor por si só, devemos dividir entre as possíveis permutações que cada país pode ter.
Como os Estados Unidos tem competidores, então tem permutações possíveis de seus jogadores. De maneira similar, a Rússia tem 
, a Índia 
e finalmente, a Espanha 
. Portanto, os rankings possíveis estão dados por
Variações
Quantos números de três dígitos podem ser formados com os números: 
?
a) Primeiro dígito
Temos que separar o número em dois blocos:
No primeiro bloco, de um número, pode ser ocupado apenas um dos dígitos porque um número não começa por zero (exceto os de matrículas, os da loteria e outros casos particulares),
b) Segundo e terceiro dígito
O segundo bloco, de dois números, pode ser ocupado por qualquer dígito.
Em ambos casos:
Sim, entram todos os elementos.
Sim, importa a ordem.
Sim, os elementos se repetem.
Pelas características, trata-se de uma variação.
As maneiras de preencher o primeiro bloco multiplicado pelas maneira de escolher o segundo nos dá o total de números com dígitos
Com o (.ponto, _ linha) do sistema Morse, quantos sinais diferentes podemos enviar usando no máximo quatro pulsos?
Usando no máximo pulsos, existem casos que devemos considerar: sinais com , com , com ou com pulsos.
Não. Neste caso não entram todos os elementos de sinais com pulso mas, sim, entram nos outros.
Sim, importa a ordem.
Sim, os elementos se repetem.
Pelas característica, trata-se de uma variação com repetição.
De quantas formas diferentes podem ser ocupados os postos de presidente, vice presidente e tesoureiro de um clube de futebol, sabendo que existem 
candidatos possíveis?
Não. Não entram todos os elementos.
Sim, importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma variação.
Encontre o número de capicuas (números que se lê igual de frente pra trás e de trás pra frente: 11, 99, 232, 171, 1441...) com oito dígitos. Quantas capicuas existem com nove dígitos?
Números capicuas (ou número palíndromo) são números com uma propriedade na qual são lidos do mesmo modo da esquerda para direita ou da direita para a esquerda.
a) Capicuas de dígitos 
Como os números a partir da quinta está determinada pelas primeiras, então o número de capicuas de oito dígitos coincide com os dos números de dígitos. Assim, temos que ver de quantas maneiras podemos escolher os valores para a, b, c e d, com 
.
Para isso, podemos obter os números de dígitos e subtrair os que começam com 
.
Não. Não entram todos os elementos. Tenho como elementos as dígitos e me interessa designar valores para letras/espaços.
Sim, importa a ordem.
Sim, os elementos se repetem.
Pelas características, trata-se de uma variação com repetição.
b) Capicuas com dígitos
Analogamente ao caso anterior,
Considerando os números de dígitos.
No total, devo subtrair os números que iniciam com .
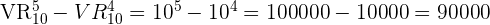
Em um campeonato mundial de futebol participam 
seleções nacionais do mundo inteiro. Se todos os países têm as mesmas possibilidades de ganhar o mundial, então de quantas maneiras possíveis podem ser formadas um campeão e vice campeão?
Não entram todos os elementos.
Sim, importa a ordem; não é mesmo que o Brasil seja campeão e a Alemanha vice campeã e que a Alemanha seja campeã e o Brasil vice campeão.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma variação.
Combinações
De quantas formas podem ser mescladas as setes cores do arco íris selecionando-as de três em três?
Não entram todos os elementos. Pois, com as formaremos grupos de .
Não importa a ordem. É uma mescla, dessa forma, vermelho, azul e amarelo dão a mesma cor que amarelo, azul e vermelho.
Não. Os elementos não se repetem. Como vamos pegar cores do arco íris, então entende-se que devem ser diferentes.
Pelas características, trata-se de uma combinação
Em uma turma com 
alunos querem eleger um comitê formado por três alunos. Quantos comitês diferentes podem ser formados?
Não entram todos os elementos. O comitê é de pessoas unicamente.
Não importa a ordem: João, Ana e Bia formam o mesmo comitê que Bia, João e Ana.
Não. Os elementos não se repetem. O comitê não pode estar formado por Bia, Bia e Bia. Uma pessoa não pode repetir a si mesma.
Pelas características, trata-se de uma combinação
Quantas apostas de Loteria de uma coluna teremos que preencher para garantir o acerto dos seis resultados entre os 
números?
Esta loteria consiste na escolha de números entre os . A loteria escolhe aleatoriamente números. Se esses números forem escolhidos por alguém que apostou, ele se torna o ganhador.Não entram todos os elementos. Levamos em consideração elementos entre os .
Não importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma combinação
Em um armazém há cinco tipos diferentes de garrafas. De quantas maneiras podemos escolher quatro garrafas?
Não entram todos os elementos. Escolhemos apenas 4.
Não importa a ordem. Dá no mesmo se escolhemos garrafas de licor e de rum, que de rum e de licor.
Sim, os elementos se repetem. Podemos escolher mais de uma garrafa do mesmo tipo
Pelas características, trata-se de uma combinação com repetição
Quantas diagonais tem um pentágono e quantos triângulos podem ser formados com suas vértices?
Determinaremos as retas que podem ser traçadas com vértices entre os disponíveis (e triângulos com vértices).
Não entram todos os elementos.
Não importa a ordem.
Não. Os elementos não se repetem
Pelas características, trata-se de uma combinação
É de 
que devemos subtrair os lados do qual formam retas que não são diagonais.
diagonais
triângulos
Um grupo composto por cinco homens e sete mulheres formam um comitê de homens e mulheres. De quantas formas podem ser formados, se:
- Pode participar nele qualquer homem ou mulher.
- Uma mulher determinada deve pertencer ao comitê.
- Dois homens determinados não podem estar no comitê.
Não entram todos os elementos.
Não importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trabalharemos com combinações.
a) Pode participar nele qualquer homem ou mulher.
b) Uma mulher determinada deve pertencer ao comitê.
c) Dois homens determinados não podem estar no comitê.
Com uma turma de nove alunos se deseja formar três equipes de três alunos cada uma. De quantas maneiras podem ser feitas?
Para este problema veremos de quantas maneiras podemos formar a primeira equipe e em seguida multiplicaremos pelas maneiras de formar a segunda equipe pelas maneiras de formar a terceira.
Não entram todos os elementos. Pois serão escolhidas pessoas das que restam disponíveis.
Não importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma combinação.
Uma pessoa tem cinco moedas com diferentes valores. Quantas somas diferentes de dinheiro podem ser formadas com as cinco moedas?
Consideramos as somas formadas por moeda, moedas, moedas, moedas ou moedasNão entram todos os elementos (Sim, no caso de que sejam usadas as moedas)
Não importa a ordem.
Não. Os elementos não se repetem.
Pelas características, trata-se de uma combinação.
Uma companhia rifa televisões iguais entre seus 
trabalhadores. De quantas formas os ganhadores podem ser escolhidos?
Como as televisões são iguais e apenas nos interessa selecionar os ganhadores, então a ordem não importa, portanto, estamos diante de uma combinação. Devemos selecionar pessoas entre as que serão as ganhadoras. Assim, o número de formas é
Quantos subconjuntos há em um conjunto de elementos?
Pela definição, há 
subconjuntos com tamanho 
em um conjunto que contém 
elementos. Portanto, procuramos subconjuntos com tamanho “zero” (o vazio), tamanho e . Assim, a resposta que procuramos é
Gostou desse artigo? Deixe uma nota!
Loading...
