
Definição de permutações
Uma permutação representa o número de maneiras diferentes de organizar os elementos de um conjunto. Se o conjunto tem  elementos e queremos organizá-los em grupos de tamanho
elementos e queremos organizá-los em grupos de tamanho  então é necessário que
então é necessário que 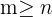 .
.
Devemos considerar os seguintes pontos:
1 A ordem dos elementos importa, pois trocar dois elementos diferentes gera uma nova permutação.
2 Os elementos não se repetem. Caso fossem repetidos ou iguais entre si, a troca entre eles não resultaria em uma nova permutação.
Para calcular o total de maneiras de dispor  elementos em
elementos em  posições distintas, usamos a fórmula:
posições distintas, usamos a fórmula:

Se em um determinado caso, 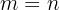 , para calcular o total de permutações utilizamos a seguinte fórmula:
, para calcular o total de permutações utilizamos a seguinte fórmula:
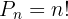
A seguir, veja alguns exemplos com base nessa definição:
Exemplos de problemas com permutações
1Calcular as permutações de  elementos em
elementos em  posicões.
posicões.
Solução
Neste caso, temos 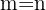 , então aplicamos:
, então aplicamos:
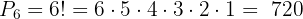
Assim, existem  maneiras diferentes de organizar
maneiras diferentes de organizar  elementos.
elementos.
2Quantos números de 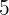 algarismos diferentes podem ser formados com os dígitos:
algarismos diferentes podem ser formados com os dígitos: 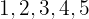 ?
?
Solução:
Como temos  dígitos diferentese queremos formar números com cinco algarismos, temos
dígitos diferentese queremos formar números com cinco algarismos, temos 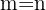 então aplicamos:
então aplicamos:

Portanto, existem  números diferentes com cinco algarismos formados a partir dos dígitos
números diferentes com cinco algarismos formados a partir dos dígitos  .
.
3De quantas maneiras diferentes 8 pessoas podem se sentar em uma fila com 8 cadeiras?
Solução:
Como temos  pessoas diferentes e 8 cadeiras, e já que não tem indicação de dois iguais e querem sentar em 8 cadeiras, então
pessoas diferentes e 8 cadeiras, e já que não tem indicação de dois iguais e querem sentar em 8 cadeiras, então 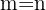 aplicamos:
aplicamos:
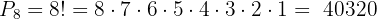
Portanto, existem 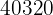 maneiras diferentes de sentar as 8 pessoas.
maneiras diferentes de sentar as 8 pessoas.
4De quantas maneiras diferentes 8 pessoas podem se sentar em uma fila com 7 cadeiras?
Solução:
Como temos  pessoas e essas são diferentes, já que não há indicaçao de não indicação que tem dois iguais e que querem se sentar em
pessoas e essas são diferentes, já que não há indicaçao de não indicação que tem dois iguais e que querem se sentar em  cadeiras
cadeiras  , então aplicamos:
, então aplicamos:
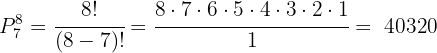
Assim, existem 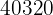 maneiras diferentes de sentar 8 pessoas em 7 cadeiras, sempre sobra uma pessoa de fora.
maneiras diferentes de sentar 8 pessoas em 7 cadeiras, sempre sobra uma pessoa de fora.
5De quantas maneiras diferentes 8 pessoas podem se sentar em uma fila com 5 cadeiras?
Solución:
Como temos  pessoas todas diferentes e não indicam se há repetições que querem se sentar em
pessoas todas diferentes e não indicam se há repetições que querem se sentar em  cadeiras
cadeiras  então:
então:
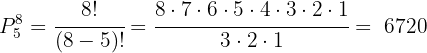
Dessa forma, existem 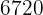 maneiras diferentes de sentar 8 pessoas em 5 cadeiras.
maneiras diferentes de sentar 8 pessoas em 5 cadeiras.
6Quantas formas diferentes existem de posicionar as letras  em três posições?
em três posições?
Solução:
Neste caso 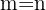 vamos aplicar:
vamos aplicar:

Assim, existem  maneiras diferentes de organizar as letras
maneiras diferentes de organizar as letras 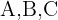 , que são
, que são

7Se temos  elementos e queremos posicioná-los em
elementos e queremos posicioná-los em 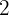 lugares, de quantas maneiras isso pode ser feito?
lugares, de quantas maneiras isso pode ser feito?
Solução:
Neste caso  , então aplicamos:
, então aplicamos:
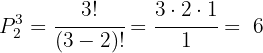
Portanto, há  maneiras diferentes de organizar 3 elementos em 2 posições. Se chamarmos os elementos de
maneiras diferentes de organizar 3 elementos em 2 posições. Se chamarmos os elementos de 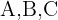 as possíveis arrumações são:
as possíveis arrumações são:
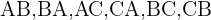
8Se temos 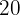 alunos e queremos formar uma comissão com
alunos e queremos formar uma comissão com  alunos, quantas comissões distintas podemos formar?
alunos, quantas comissões distintas podemos formar?
Solución:
Neste caso  aplicamos:
aplicamos:
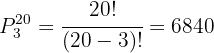
Portanto, existem 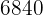 maneiras diferentes de organizar 20 alunos em comissões de 3 pessoas, considerando a ordem.
maneiras diferentes de organizar 20 alunos em comissões de 3 pessoas, considerando a ordem.
As permutações têm inúmeras aplicações, especialmente quando lidamos com contagens complexas que podem ser simplificadas com essa ferramenta.
É importante lembrar que nas permutações a ordem dos elementos importa.
E você, já percebeu onde usa permutações no seu dia a dia?
Resumir com IA:












