Calcule as probabilidades pedidas dada a seguinte informação:
Seja  e
e  dois eventos aleatórios com
dois eventos aleatórios com
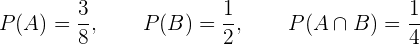
Encontre:
1 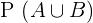
2 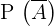
3 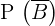
4 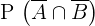
5 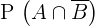
6 
7 
Seja  e
e  dois eventos aleatórios com
dois eventos aleatórios com
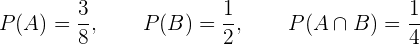
Encontre:
1 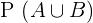
Os eventos são compatíveis porque a interseção é diferente do vazio, 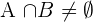 , dado que sua probabilidade é nula. Portanto
, dado que sua probabilidade é nula. Portanto
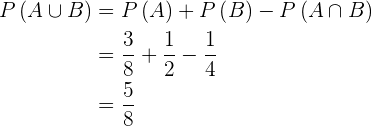
2 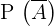
As probabilidades de  é igual a
é igual a  (probabilidade total) menos a probabilidade do evento
(probabilidade total) menos a probabilidade do evento 
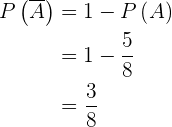
3 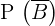
A probabilidade de 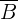 é igual a
é igual a  (probabilidade total) menos a probabilidade do evento
(probabilidade total) menos a probabilidade do evento 
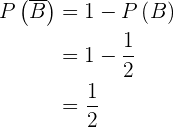
4 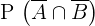
Aplicando as leis de Morgan, obtemos
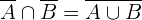
Além disso, a probabilidade de 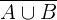 é igual a
é igual a  (probabilidade total) menos a probabilidade do evento
(probabilidade total) menos a probabilidade do evento 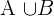 , portanto
, portanto
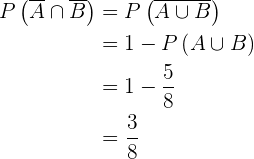
5 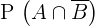
Podemos notar que  . Aplicando a probabilidade da diferença de eventos, temos
. Aplicando a probabilidade da diferença de eventos, temos
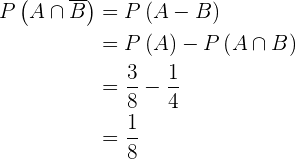
6 
Aplicando as leis de Morgan, obtemos

Além disso, a probabilidade de  é igual a
é igual a  (probabilidade total) menos a probabilidade do evento
(probabilidade total) menos a probabilidade do evento 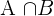 , portanto
, portanto
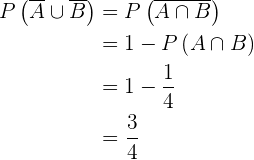
7 
Podemos notar que 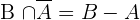 . Aplicando a probabilidade da diferença de eventos, temos
. Aplicando a probabilidade da diferença de eventos, temos
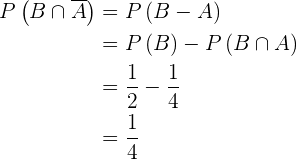
Calcule o que se pede dados os seguintes eventos e suas probabilidades.

Encontre:
1 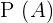
2 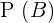
3 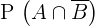
4 
Calcule o que se pede dados os seguintes eventos e suas probabilidades.

Encontre:
1 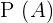
A probabilidade de  é igual a
é igual a  (probabilidade total) menos a probabilidade do evento
(probabilidade total) menos a probabilidade do evento 
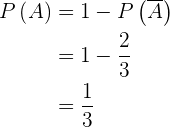
2 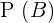
Vale recordar que 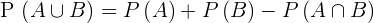 , portanto, se isolamos
, portanto, se isolamos 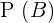 obtemos
obtemos
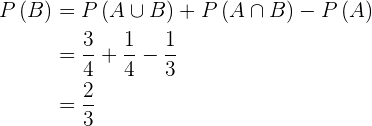
3 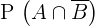
Podemos notar que  . Aplicando a probabilidade da diferença de eventos, temos
. Aplicando a probabilidade da diferença de eventos, temos
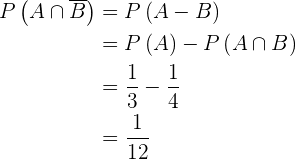
4 
Podemos notar que 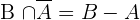 . Aplicando a probabilidade da diferença de eventos, temos
. Aplicando a probabilidade da diferença de eventos, temos
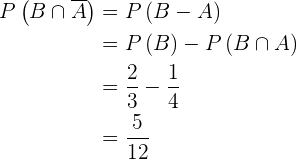
Descreva o espaço amostral dado o seguinte experimento.
Duas bolas são retiradas de uma urna que contém em seu interior uma bola branca, uma bola vermelha, uma bola verde e uma bola preta. Descreva o espaço amostral nas seguintes situações:
1 A primeira bola vai de volta para a urna antes de se retirar a segunda bola.
2 A primeira bola não volta para a urna.
Duas bolas são retiradas de uma urna que contém em seu interior uma bola branca, uma bola vermelha, uma bola verde e uma bola preta. Descreva o espaço amostral nas seguintes situações:
1 A primeira bola vai de volta para a urna antes de se retirar a segunda bola.
2 A primeira bola não volta para a urna.
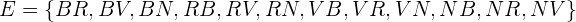
Calcule as probabilidades indicadas segundo o seguinte experimento:
Uma urna tem oito bolas vermelhas, cinco bolas amarelas e sete bolas verdes. Se retirarmos uma bola ao acaso calcule a probabilidade de que ela:
1 Seja vermelha.
2 Seja verde.
3 Seja amarela.
4 Não seja vermelha.
5 Não seja amarela.
Uma urna tem oito bolas vermelhas, cinco bolas amarelas e sete bolas verdes. Se retirarmos uma bola ao acaso calcule a probabilidade de que ela:
1 Seja vermelha.
- Casos favoráveis:
 .
.
Casos possíveis: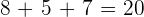 .
.
Portanto, a probabilidade é
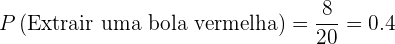
2 Seja verde.
- Casos favoráveis:
 .
.
Casos possíveis: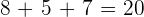 .
.
Portanto, a probabilidade é
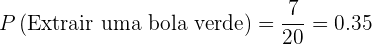
3 Seja amarela.
- Casos favoráveis:
 .
.
Casos possíveis: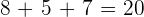 .
.
Portanto, a probabilidade é
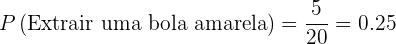
4 De que não seja vermelha.
- Casos favoráveis:
 .
.
Casos possíveis: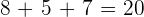 .
.
Portanto, a probabilidade é
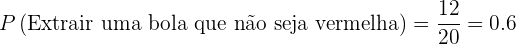
5 Que não seja amarela.
- Casos favoráveis:
 .
.
Casos possíveis: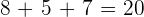 .
.
Portanto, a probabilidade é
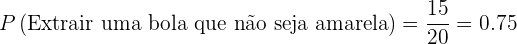
Calcule as probabilidades indicadas segundo o seguinte experimento:
Uma urna contém três bolas vermelhas e sete bolas brancas. São retiradas duas bolas ao acaso. Escreva o espaço amostral e encontre a probabilidade dos eventos:
1 Com reposição (tiramos a primeira bola e a colocamos de volta antes de retirar a segunda bola).
2 Sem reposição (tiramos a primeira bola e não a colocamos de volta. Em seguida tiramos uma segunda bola das que restaram).
Uma urna contém três bolas vermelhas e sete bolas brancas. São retiradas duas bolas ao acaso. Escreva o espaço amostral e encontre a probabilidade dos eventos:
1 Com reposição (tiramos a primeira bola e a colocamos de volta antes de retirar a segunda bola).
O espaço amostral está dado por

A extração de duas bolas com reposição são eventos independentes, já que a extração da primeira bola não tem nenhum efeito sobre a segunda, portanto
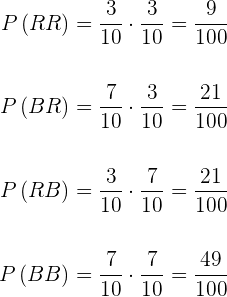
2 Sem reposição (tiramos a primeira bola e não a colocamos de volta. Em seguida tiramos uma segunda bola das que restaram).
O espaço amostral está dado por

A extração de duas bolas com reposição são eventos dependentes, já que a extração da primeira bola afeta a extração da segunda, portanto
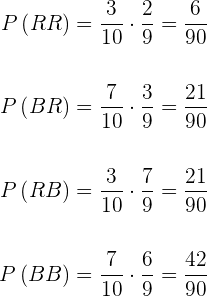
Calcule as probabilidades indicadas segundo o seguinte experimento:
Retiramos uma bola de uma urna que contém em seu interior quatro bolas vermelhas, cinco bolas brancas e seis pretas.
1 Qual é a probabilidade de que a bola seja vermelha ou branca?
2 Qual é a probabilidade de que não seja branca?
Retiramos uma bola de uma urna que contém em seu interior quatro bolas vermelhas, cinco bolas brancas e seis pretas.
1 Qual é a probabilidade de que a bola seja vermelha ou branca?
A extração de duas bolas de cores diferentes são eventos incompatíveis, ou seja, sua interseção é um conjunto vazio. Portanto
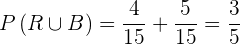
2 Qual é a probabilidade de que não seja branca?
Devemos lembrar que a probabilidade dos eventos 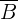 é igual a
é igual a  menos a probabilidade do evento
menos a probabilidade do evento  , assim
, assim

Resolva os seguintes problemas:
Uma sala de aula possui  alunos, dos quais
alunos, dos quais  são loiras,
são loiras,  morenas,
morenas,  loiros e
loiros e  morenos. Encontre a probabilidade de que um aluno:
morenos. Encontre a probabilidade de que um aluno:
1 Seja um homem.
2 Seja uma mulher morena.
3 Seja homem ou mulher.
Uma sala de aula possui  alunos, dos quais
alunos, dos quais  são loiras,
são loiras,  morenas,
morenas,  loiros e
loiros e  morenos. Encontre a probabilidade de que um aluno:
morenos. Encontre a probabilidade de que um aluno:
1 Seja um homem.
- Casos favoráveis:
 .
.
Casos possíveis: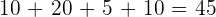 .
.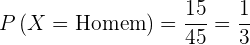
2 Seja uma mulher morena.
- Casos favoráveis:
 .
.
Casos possíveis: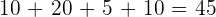 .
.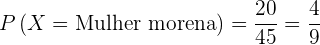
3 Seja homem ou mulher.
- Casos favoráveis:
 .
.
Casos possíveis: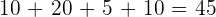 .
.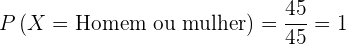
Um dado está manipulado de forma que as probabilidades de tirar os diferentes lados são proporcionais aos seus próprios números.
Encontre:
1 A probabilidade de tirar o 6 em um lançamento.
2 A probabilidade de tirar um número ímpar em um lançamento.
Um dado está manipulado de forma que as probabilidades de tirar os diferentes lados são proporcionais aos seus próprios números.
Encontre:
1 A probabilidade de tirar o 6 em um lançamento.
Vamos chamar de  a probabilidade. Sabendo que é proporcional aos números dos dados, obteremos:
a probabilidade. Sabendo que é proporcional aos números dos dados, obteremos: 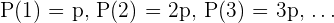 . Além disso, a sua soma cumpre
. Além disso, a sua soma cumpre
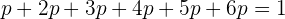
Isolando  obtemos
obtemos
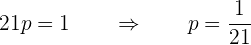
Portanto, 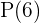 é
é
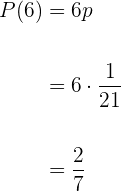
2 A probabilidade de tirar um número ímpar em um lançamento.
Os números ímpares seriam,  e
e  , portanto, a probabilidade está dada por
, portanto, a probabilidade está dada por
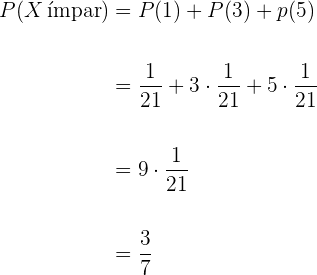
Dois dados são lançados no ar e a soma de seus pontos anotados. Pede-se:
1 A probabilidade de que saia o  .
.
2 A probabilidade de que o número seja par.
3 A probabilidade de que o número seja múltiplo de três.
Dois dados são lançados no ar e a soma de seus pontos anotados. Pede-se:
1 A probabilidade de que saia o  .
.
Casos favoráveis: Os casos favoráveis são os  seguintes
seguintes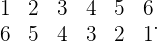
Casos possíveis: Para encontrar os casos possíveis devemos calcular as variações com a repetição de  elementos de
elementos de  em
em  ,
, .
.
Assim, a probabilidade de que os dados somem  é
é
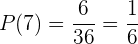 .
.
2 A probabilidade de que o número seja par.
Casos possíveis: Com o cálculo anterior sabemos que os casos possíveis são  .
.
Casos favoráveis: A quantidade de casos favoráveis dos quais a soma é par é a metade dos casos possíveis. Além de que a soma dos números pares é par e a soma dos números ímpares é par. Portanto os casos favoráveis são  .
.
Dada a premissa acima, a probabilidade de que a soma seja par é
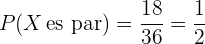 .
.
3 A probabilidade de que o número seja múltiplo de três.
Casos favoráveis: Os casos favoráveis são os  seguintes
seguintes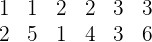
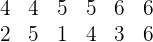
Casos possíveis: Com os cálculos anteriores sabemos que os casos possíveis são  .
.
Assim, a probabilidade de que os dados somem um múltiplo de  é
é
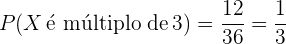 .
.
São lançados três dados. Encontre a probabilidade de que:
1 Saia  em todos.
em todos.
2 Os pontos somem  .
.
São lançados três dados. Encontre a probabilidade de que:
1 Saia  em todos.
em todos.
Casos favoráveis: Temos apenas um caso favorável.
Casos possíveis: Para encontrar os casos possíveis devemos calcular as variações com repetição de  elementos de
elementos de  em
em  ,
,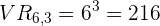 .
.
Assim, a probabilidade de que todos os dados sejam  é
é
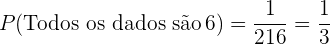 .
.
2 Os pontos somem  .
.
Casos favoráveis: Os casos favoráveis são os  seguintes
seguintes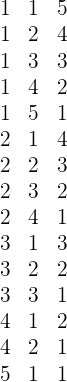
Casos possíveis: Com o cálculo anterior sabemos que os casos possíveis são  .
.
Assim, a probabilidade de que os dados somem  é
é
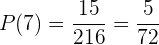 .
.
Encontre a probabilidade de que ao levantarmos nossas peças de dominó obtemos um número de pontos maior do que  ou múltiplo de
ou múltiplo de  .
.
Encontre a probabilidade de que ao levantarmos nossas peças de dominó obtemos um número de pontos maior do que ou múltiplo de
ou múltiplo de  .
.
O evento com peças de dominó do qual conseguimos um número de pontos maior do que  está dado por
está dado por
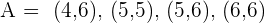
O evento com peças de dominó do qual conseguimos um número de pontos maior do que  está dado por
está dado por
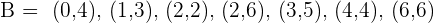
Portanto, devemos considerar que o evento final é 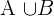 . Além disso, um jogo de dominó é composto por
. Além disso, um jogo de dominó é composto por  peças, portanto, a probabilidade está dada por
peças, portanto, a probabilidade está dada por
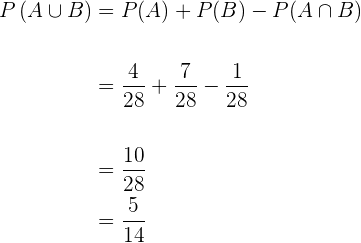
Encontre a probabilidade de que ao jogarmos um dado no ar, saia:
1 Um número par.
2 Um número múltiplo de três.
3 Um número maior que quatro.
Encontre a probabilidade de que ao jogarmos um dado no ar, saia:
1 Um número par.
Casos favoráveis: Os casos favoráveis são os  seguintes
seguintes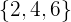
Casos possíveis: Por ser um dado de  lados, temos
lados, temos  casos favoráveis.
casos favoráveis.
Dada a premissa acima, a probabilidade é
 .
.
2 Um número múltiplo de três.
Casos favoráveis: Os casos favoráveis são os  seguintes
seguintes
Casos possíveis: Por ser um dado de  lados, temos
lados, temos  casos favoráveis.
casos favoráveis.
Dada a premissa acima, a probabilidade é
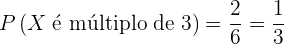 .
.
3 Um número maior que quatro.
Casos favoráveis: Os casos favoráveis são os  seguintes
seguintes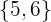
Casos possíveis: Por ser um dado de  lados, temos
lados, temos casos favoráveis.
casos favoráveis.
Dada a premissa acima, a probabilidade é
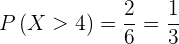 .
.
Encontre a probabilidade de que ao jogarmos duas moedas no ar, saia:
1 Duas caras.
2 Duas coroas.
3 Uma cara e uma coroa.
Encontre a probabilidade de que ao jogarmos duas moedas no ar, saia:
1 Duas caras.

São eventos independentes, portanto, uma vez que a probabilidade de que cada moeda seja cara é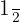 , assim
, assim

2 Duas coroas.

Igual ao cálculo anterior são eventos independentes portanto uma vez que a probabilidade de que cada moeda seja coroa é 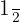 , assim
, assim
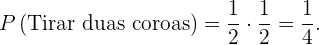
3 Uma cara e uma coroa.

A probabilidade de obtermos uma cara e uma coroa é a probabilidade de obter o evento  . Além disso igual que nos cálculos anteriores são eventos independentes portanto dado que a probabilidade de que cada moeda seja coroa ou cara é
. Além disso igual que nos cálculos anteriores são eventos independentes portanto dado que a probabilidade de que cada moeda seja coroa ou cara é 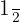 , assim
, assim
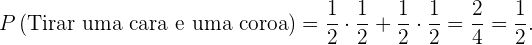
Em um envelope há  folhas, em
folhas, em  delas tem um carro desenhado e as restantes estão em branco. Encontre a probabilidade de se extrair pelo menos uma folha com o desenho de um carro:
delas tem um carro desenhado e as restantes estão em branco. Encontre a probabilidade de se extrair pelo menos uma folha com o desenho de um carro:
1 Se retirarmos uma folha.
2 Se retirarmos duas folhas.
3 Se retirarmos três folhas.
Em um envelope há  folhas, em
folhas, em  delas tem um carro desenhado e as restantes estão em branco. Encontre a probabilidade de se extrair pelo menos uma folha com o desenho de um carro:
delas tem um carro desenhado e as restantes estão em branco. Encontre a probabilidade de se extrair pelo menos uma folha com o desenho de um carro:
1 Se retirarmos uma folha.
Temos  casos favoráveis e
casos favoráveis e  possíveis, portanto
possíveis, portanto
 .
.
2 Se retirarmos duas folhas.
A probabilidade de que ao retirarmos  folhas ao menos uma tenha um carro é igual a
folhas ao menos uma tenha um carro é igual a  menos a probabilidade de que ao retirarmos
menos a probabilidade de que ao retirarmos  folhas as duas estejam em branco. Portanto
folhas as duas estejam em branco. Portanto
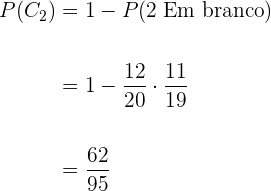
3 Se retirarmos três folhas.
A probabilidade de que ao retirarmos  folhas ao menos uma tenha um carro é igual a
folhas ao menos uma tenha um carro é igual a  menos a probabilidade de que ao retirarmos
menos a probabilidade de que ao retirarmos  folhas todas estejam em branco. Portanto
folhas todas estejam em branco. Portanto
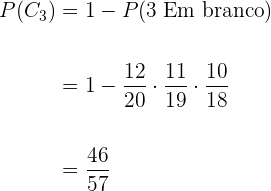
Os estudantes  e
e  têm respectivamente probabilidades
têm respectivamente probabilidades 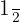 e
e  de reprovarem em uma prova. A probabilidade que de sejam reprovados simultaneamente é de
de reprovarem em uma prova. A probabilidade que de sejam reprovados simultaneamente é de  . Determine a probabilidade de que ao menos um dos estudantes seja reprovado.
. Determine a probabilidade de que ao menos um dos estudantes seja reprovado.
Devemos notar que são eventos compatíveis porque 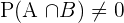 . Portanto
. Portanto
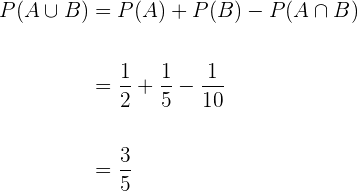
Dois irmãos saem para caçar. O primeiro mata por volta de  alvos a cada
alvos a cada  disparos e o segundo
disparos e o segundo  um alvo a cada
um alvo a cada  disparos. Se os dois disparam ao mesmo tempo em um mesmo alvo qual é a probabilidade de que matem esse alvo?
disparos. Se os dois disparam ao mesmo tempo em um mesmo alvo qual é a probabilidade de que matem esse alvo?
Dois irmãos saem para caçar. O primeiro mata por volta de  alvos a cada
alvos a cada  disparos e o segundo
disparos e o segundo  um alvo a cada
um alvo a cada  disparos. Se os dois disparam ao mesmo tempo em um mesmo alvo qual é a probabilidade de que matem esse alvo?
disparos. Se os dois disparam ao mesmo tempo em um mesmo alvo qual é a probabilidade de que matem esse alvo?
Primeiro calculamos a probabilidade de que ambos matem um alvo. Ou seja
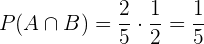
Dada a premissa anterior, vemos que os eventos são compatíveis. Portanto
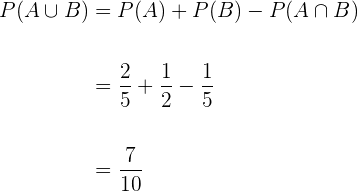
Em uma sala de aula há  homens e
homens e  mulheres; a metade dos homens e a metade das mulheres tem olhos castanhos. Determine a probabilidade de que uma pessoa escolhida ao acaso seja um homem ou tenha os olhos castanhos.
mulheres; a metade dos homens e a metade das mulheres tem olhos castanhos. Determine a probabilidade de que uma pessoa escolhida ao acaso seja um homem ou tenha os olhos castanhos.
Em uma sala de aula há  homens e
homens e  mulheres; a metade dos homens e a metade das mulheres tem olhos castanhos. Determine a probabilidade de que uma pessoa escolhida ao acaso seja um homem ou tenha os olhos castanhos.
mulheres; a metade dos homens e a metade das mulheres tem olhos castanhos. Determine a probabilidade de que uma pessoa escolhida ao acaso seja um homem ou tenha os olhos castanhos.

Dada a planilha anterior, a probabilidade é
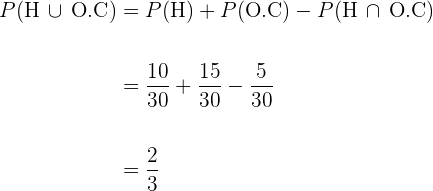
A probabilidade de que um homem viva  anos é
anos é  e a de que sua mulher viva
e a de que sua mulher viva  anos é
anos é  . Calcule a probabilidade:
. Calcule a probabilidade:
1 De que ambos vivam  anos.
anos.
2 De que o homem viva  anos e sua mulher não.
anos e sua mulher não.
3 De que ambos morram antes dos  anos.
anos.
A probabilidade de que um homem viva  anos é
anos é  e a de que sua mulher viva
e a de que sua mulher viva  anos é
anos é  . Calcule a probabilidade:
. Calcule a probabilidade:
1 De que ambos vivam  anos.
anos.
Primeiro, devemos notar que são eventos independentes, portanto
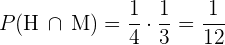
2 De que o homem viva  anos e sua mulher não.
anos e sua mulher não.
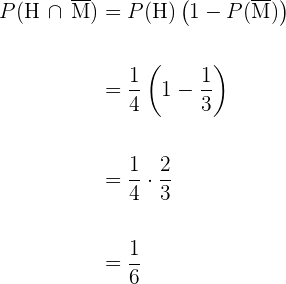
3 De que ambos morram antes dos  anos.
anos.
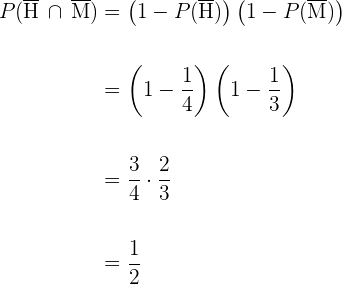
Resumir com IA:


