Passo a passo do método de redução
Método de Redução para Sistemas de Equações: passos do método de redução.
Para resolver um sistema de equações pelo método de redução, siga os seguintes passos:
- Preparam-se as duas equações, multiplicando-as por um número de forma que as equações resultantes tenham um coeficiente em comum.
- Realiza-se uma subtração (ou adição, dependendo dos sinais dos coeficientes) para desaparecer (eliminar) uma das incógnitas.
- Resolve-se a equação resultante.
- O valor obtido é substituído em uma das equações iniciais e faz-se a operação.
- Os dois valores obtidos compõe a solução do sistema.
Exemplos do método de redução
Neste caso, existem duas maneiras de resolver o sistema de equações a seguir:
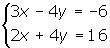
Por multiplicação
1 Eliminamos o x multiplicando a primeira equação por 2 e a segunda por −3
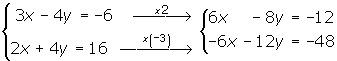
2 À equação acima, somamos a equação abaixo e resolvemos a equação.
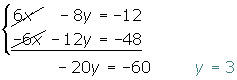
3 Substituímos o valor de y em uma das 2 equações iniciais, neste caso, a segunda.
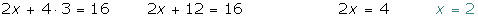
4 O resultado é:
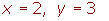
Somando (ou subtraindo) diretamente das equações
Como esta equação nos permite eliminar o
sem a necessidade de multiplicação, podemos realizar a soma das equações sem prepará-las, ao contrário do método anterior.
1 Somamos termo a termo das equações
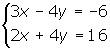
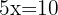
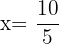
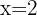
2 Substituímos o valor de x em uma das 2 equações iniciais, neste caso, escolhemos a primeira.
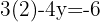
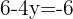
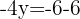
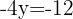
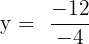
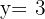
Podemos observar que em ambos os casos, os resultados são iguais.
Gostou desse artigo? Deixe uma nota!
Loading...
aula boa eu tire 10 na prova
🙌