Temas

Definição da eliminação de Gauss (Método de Gauss-Jordan)
A eliminação de Gauss consiste em transformar um sistema de equações em outro equivalente, de modo que este assuma a forma escalonada.
Para facilitar os cálculos, vamos transformar o sistema em uma matriz, na qual colocaremos os coeficientes das variáveis e os termos independentes (separados por uma barra vertical).

Sistemas de equações equivalentes
Obtemos sistemas equivalentes por meio da eliminação de equações dependentes se ocorrer alguma das seguintes situações:
1 Todos os coeficientes são iguais a zero.
2 Duas linhas são idênticas.
3 Uma linha é proporcional a outra.
4 Todos os coeficientes são iguais a zero.
Critérios de equivalência de sistemas de equações
1 Se somamos ou subtraimos uma mesma expressão em ambos os membros de uma equação de um sistema, o sistema resultante será equivalente ao original.
2 Se multiplicamos ou dividimos ambos os membros das equações de um sistema por um número diferente de zero, o sistema resultante será equivalente ao original.
3 Se somamos ou subtrairmos a uma equação do sistema outra equação do mesmo sistema, o sistema resultante será equivalente ao original.
4 Se, em um sistema, substituímos uma equação por outra que resulta da soma de duas equações previamente multiplicadas ou divididas por números não nulos, o novo sistema será equivalente ao primeiro.
5 Se trocarmos a ordem das equações ou a ordem das incógnitas em um sistema, obtemos outro sistema equivalente.
Exemplo: 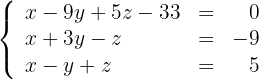
Somamos  em ambos os membros da primeira equação e obtemos:
em ambos os membros da primeira equação e obtemos:
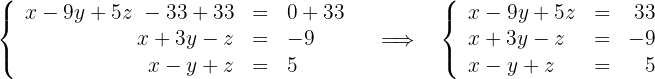
Pelo primeiro critério de equivalência, temos que o sistema original é equivalente ao sistema:
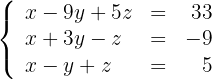
Exemplo: 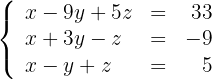
Multiplicamos por  ambos os membros das equações e, pelo segundo critério de equivalência, temos que o sistema original é equivalente ao novo sistema obtido:
ambos os membros das equações e, pelo segundo critério de equivalência, temos que o sistema original é equivalente ao novo sistema obtido:

Exemplo: 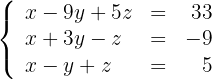
Somamos a terceira equação à segunda equação, obtemos um sistema de equações que, pelo critério 3, é equivalente com o sistema original.
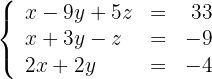
Exemplo: 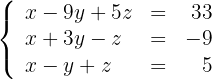
Substituímos a segunda equação pela soma da primeira equação com a segunda equação multiplicada por três. Obtemos um sistema de equações que, pelo critério 4, é equivalente ao sistema original:

Exemplo: 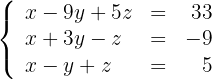
Trocamos a segunda e a terceira equação. Obtemos um sistema de equações que, pelo critério 5, é equivalente ao sistema original:

Para resolver um sistema de equações, utilizamos os critérios anteriores, como veremos nos próximos exercícios.
Exercícios de sistemas de equações
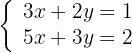
1 Escrevemos na forma matricial:
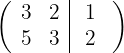
2 Substituímos a linha 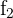 por
por 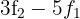 e obtemos, pelo critério 4, a matriz equivalente:
e obtemos, pelo critério 4, a matriz equivalente:
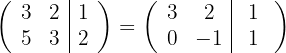
3 Substituímos a linha  por
por 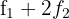 e obtemos, pelo critério 4, a matriz equivalente:
e obtemos, pelo critério 4, a matriz equivalente:
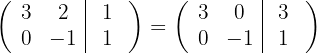
4 Substituímos as linhas 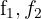 por
por 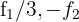 respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
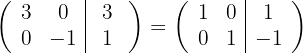
5 Temos que o sistema original é possível e determinado, e suas soluções são:
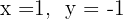
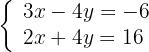
1 Escrevemos na forma matricial:
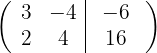
2 Substituímos a linha 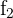 por
por 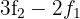 e obtemos, pelo critério 4, a matriz equivalente:
e obtemos, pelo critério 4, a matriz equivalente:
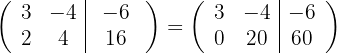
3 Substituímos a linha  por
por 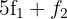 e obtemos, pelo critério 4, a matriz equivalente:
e obtemos, pelo critério 4, a matriz equivalente:
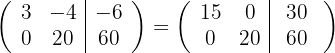
4 Substituímos as linhas 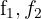 por
por 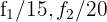 respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
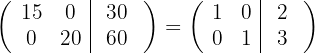
5 Temos que o sistema original é possível e determinado, e suas soluções são:
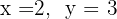
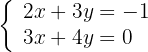
1 Escrevemos na forma matricial:
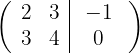
2 Substituímos a linha 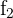 por
por 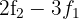 obtemos, pelo critério 4, a matriz equivalente:
obtemos, pelo critério 4, a matriz equivalente:
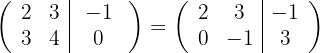
3 Substituímos a linha  por
por 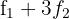 e obtemos, pelo critério 4, a matriz equivalente:
e obtemos, pelo critério 4, a matriz equivalente:
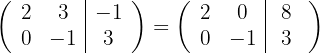
4 Substituímos as linhas 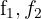 por
por 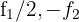 respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
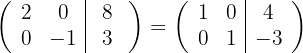
5 Temos que o sistema original é possível e determinado, e suas soluções são:
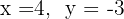
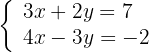
1 Escrevemos na forma matricial:
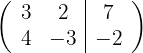
2 Substituímos a linha 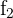 por
por 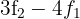 e obtemos, pelo critério 4, a matriz equivalente:
e obtemos, pelo critério 4, a matriz equivalente:
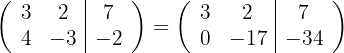
3 Substituímos a linha  por
por 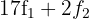 e obtemos, pelo critério 4, a matriz equivalente:
e obtemos, pelo critério 4, a matriz equivalente:
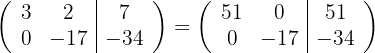
4 Substituímos as linhas 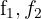 por
por 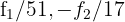 respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
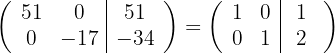
5 Temos que o sistema original é possível e determinado, e suas soluções são:
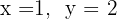
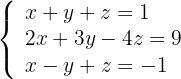
1 Escrevemos na forma matricial:
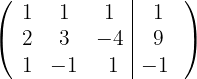
2 Substituímos as linhas  por
por  respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
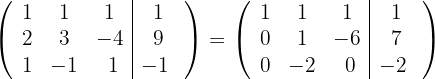
3 Trocamos as linhas  e
e  e obtemos, pelo critério 5, a matriz equivalente:
e obtemos, pelo critério 5, a matriz equivalente:
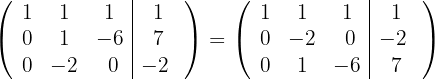
4 Substituímos as linhas 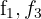 por
por 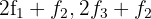 respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
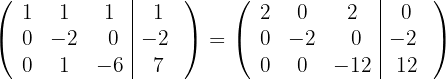
5 Substituímos as linhas  por
por 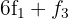 respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
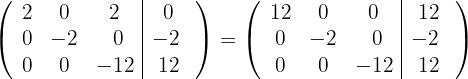
6 Substituímos as linhas  por
por 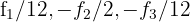 respectivamente, e obtemos, pelo critério 2, a matriz equivalente:
respectivamente, e obtemos, pelo critério 2, a matriz equivalente:
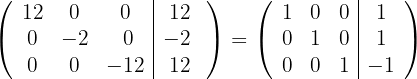
7 Temos que o sistema original é possível e determinado, e suas soluções são:
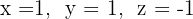
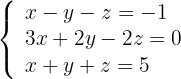
1 Escrevemos na forma matricial:
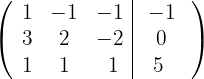
2 Substituímos as linhas  por
por 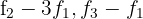 respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
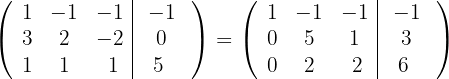
3 Substituímos as linhas 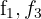 por
por 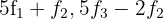 respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
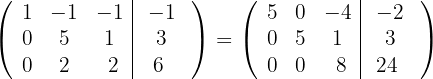
4 Substituímos as linhas 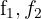 por
por 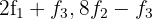 respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
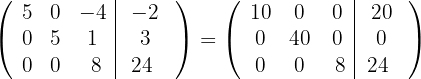
5 Substituímos as linhas  por
por 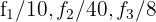 respectivamente, e obtemos, pelo critério 2, a matriz equivalente:
respectivamente, e obtemos, pelo critério 2, a matriz equivalente:
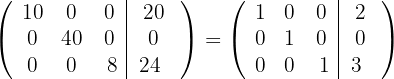
6 Temos que o sistema original é possível e determinado, e suas soluções são:
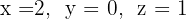
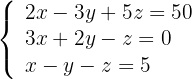
1 Escrevemos na forma matricial:
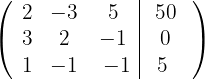
2 Trocamos as linhas  e
e  e obtemos, pelo critério 5, a matriz equivalente:
e obtemos, pelo critério 5, a matriz equivalente:
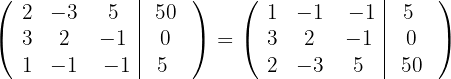
3 Substituímos as linhas  por
por 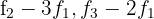 respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
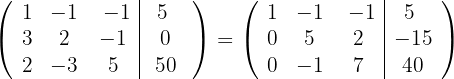
4 Substituímos as linhas 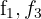 por
por 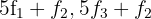 respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
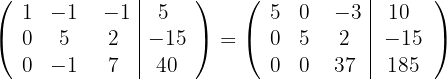
5 Substituímos as linhas 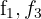 por
por 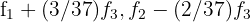 respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
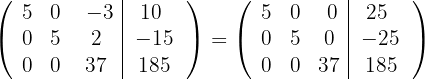
6 Substituímos as linhas  por
por 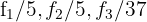 respectivamente e obtemos, pelo critério 2, a matriz equivalente:
respectivamente e obtemos, pelo critério 2, a matriz equivalente:
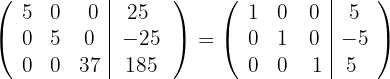
7 Temos que o sistema original é possível e determinado, e suas soluções são:
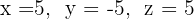
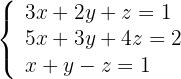
1 Escrevemos na forma matricial:
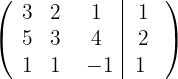
2 Trocamos as linhas  e
e  e obtemos, pelo critério 5, a matriz equivalente:
e obtemos, pelo critério 5, a matriz equivalente:
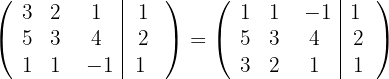
3 Substituímos as linhas  por
por  respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
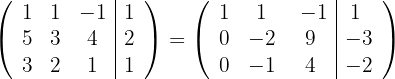
4 Substituímos as linhas 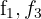 por
por  respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
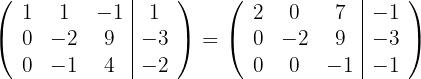
5 Substituímos as linhas 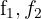 por
por 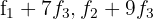 respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
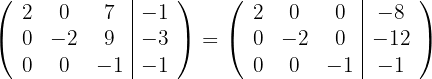
6 Substituímos as linhas  por
por 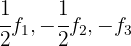 respectivamente e obtemos, pelo critério 2, a matriz equivalente:
respectivamente e obtemos, pelo critério 2, a matriz equivalente:
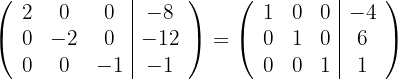
7 Temos que o sistema original é possível e determinado, e suas soluções são:
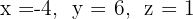

1 Escrevemos na forma matricial:
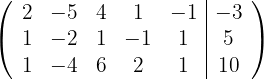
2 Trocamos as linhas  e
e  e obtemos, pelo critério 5, a matriz equivalente:
e obtemos, pelo critério 5, a matriz equivalente:
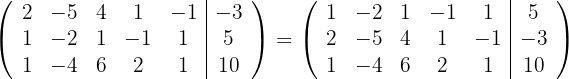
3 Substituímos as linhas  por
por  respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
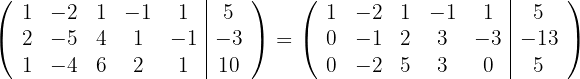
4 Substituímos as linhas 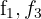 por
por  respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
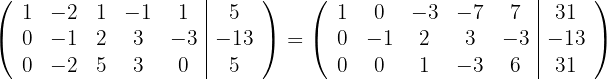
5 Substituímos as linhas 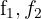 por
por  respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
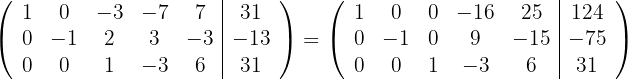
6 Obtemos que o sistema é possível e indeterminado e equivalente ao sistema original:
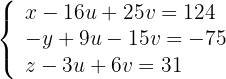
7 Multiplicamos a segunda equação por  e, pelo critério 2, obtemos o sistema equivalente:
e, pelo critério 2, obtemos o sistema equivalente:
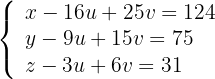
8 Fazendo  e
e  obtemos:
obtemos:


1 Escrevemos na forma matricial:
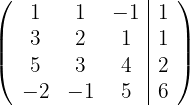
3 Substituímos as linhas 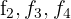 por
por  respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
respectivamente, e obtemos, pelo critério 4, a matriz equivalente:
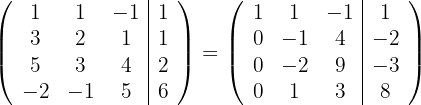
4 Substituímos as linhas  por
por  respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
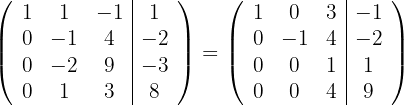
5 Substituímos as linhas  por
por 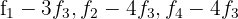 respectivamente e obtemos, pelo critério 4, a matriz equivalente:
respectivamente e obtemos, pelo critério 4, a matriz equivalente:
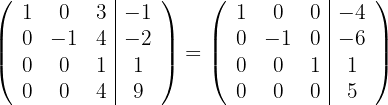
6 Como na última linha todos os coeficientes das variáveis são zero e o termo independente é diferente de zero, então o sistema é incompatível.
Resumir com IA:












X+y=-11
-X-2y=20