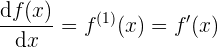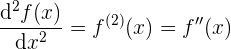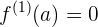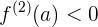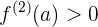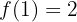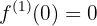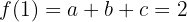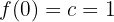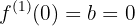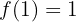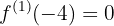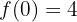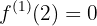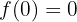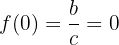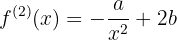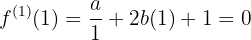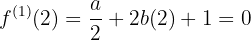Temas
Antes de começar, vamos estabelecer um conjunto de notações usuais para derivadas de uma função  .
.
O motivo de utilizarmos diferentes notações para o mesmo conceito é que, em alguns casos, os cálculos se tornam extensos ou trabalhosos, e convém adotar expressões mais curtas. O essencial é que todas representem a mesma ideia
A primeira derivada de uma função pode ser indicada por:
já a segunda derivada (a derivada da derivada) pode ser escrita como:
Neste material, para evitar confusões, usaremos a notação 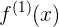 para a primeira derivada,
para a primeira derivada, 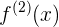 e para a segunda derivada.
e para a segunda derivada.
Uma vez definidas as notações, podemos estudar certas propriedades das funções.
De forma mais precisa, veremos os critérios que indicam onde uma função atinge seus valores máximos ou mínimos em uma determinada região. Esses pontos são chamados de máximos ou mínimos relativos.

Extremos relativos
Primeiro, vamos identificar o tipo de ponto que queremos localizar. Em termos simples, tratam-se dos pontos em que uma função atinge um valor máximo ou mínimo em comparação com valores próximos. Tais pontos recebem o nome de extremos relativos.
Se 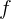 é uma função derivável em
é uma função derivável em 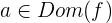 , então
, então  é um extremo relativo ou local se:
é um extremo relativo ou local se:
Máximos relativos
Se 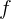 é uma função derivável em
é uma função derivável em 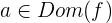 , então
, então  é um máximo relativo se:
é um máximo relativo se:
Mínimos relativos
Se 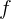 é uma função derivável em
é uma função derivável em 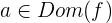 , então
, então  é um mínimo relativo se:
é um mínimo relativo se:
Cálculo de máximos e mínimos
Vamos considerar a função 
Para determinar os extremos relativos, seguimos os passos:
1Encontramos a primeira derivada da função e calculamos as raízes.
Primeiro, a derivada da função:

Agora as raízes, resolvendo a equação:
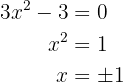
Logo, as raízes são:

2Descobrimos a segunda derivada e verificamos o sinal nas raízes
Calculamos a segunda derivada da função:

Avaliamos as raízes obtidas na segunda derivada:
 ,
,  en
en  a função tem um máximo relativo.
a função tem um máximo relativo.
 ,
,  en
en  a função tem um mínimo relativo.
a função tem um mínimo relativo.
3Calcular as imagens (da função) dos extremos relativos.
 ,
, logo em
logo em  o gráfico da função, há um máximo relativo.
o gráfico da função, há um máximo relativo.
 ,
,  logo em
logo em  o gráfico da função, há um mínimo relativo.
o gráfico da função, há um mínimo relativo.
Estudo dos extremos relativos a partir do crescimento
Se já estudamos os intervalos de crescimento e decrescimento de uma função, então:
- Há um máximo em um ponto quando a função passa de crescente
 a decrescente
a decrescente  .
. - Há um mínimo em um ponto quando a função passa de decrescente
 a crescente
a crescente  .
.
Exemplo:
Vamos considerar a seguinte função: 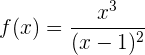
Para encontrar os extremos relativos seguiremos os seguintes passos:
1Determinar o domínio da função, a primeira derivada e suas raízes.
Primeiro o domínio da função.
Vamos encontrar os pontos onde a equação fica indeterminada, ou seja, 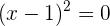
O denominador se anula em  logo
logo 
Resolvendo a derivada:

Agora as raízes, resolvendo a equação:
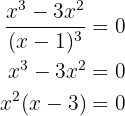
As raízes são:

2Pegamos os valores calculados e geramos partes da reta real.
Depois, pegamos um valor de cada setor, vamos avaliar na primeira derivada e observamos os sinais obtidos com a finalidade de analisar a natureza da função em cada setor.
Usamos os valores calculados e geramos os setores na reta real
Os valores são: 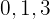 então os setores são
então os setores são 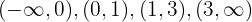
Verificando o sinal em cada intervalo:
- Seja
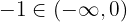 , então
, então 
 em
em  a função é crescente
a função é crescente 
- Sea
 , então
, então 
 em
em  a função é crescente
a função é crescente 
- Seja
 , então
, então 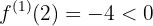
 em
em 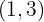 a função é decrescente
a função é decrescente 
- Seja
 , então
, então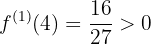
 em
em 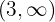 a função é crescente
a função é crescente 
Na tabela a seguir, é possível ver a informação obtida:
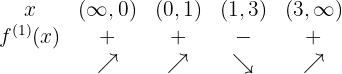
3Interpretamos a informação e identificamos máximos ou mínimos.
Observamos que foram gerados duas trocas de sinais, que está 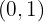 e
e 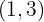 e vamos descartar porque não está definida.
e vamos descartar porque não está definida.
A próxima troca de sinal 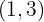 a
a 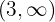 , e como é de decrescente para crescente então
, e como é de decrescente para crescente então 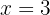 existe um mínimo relativo.
existe um mínimo relativo.
4Avaliar o ponto na função para conhecer o ponto no plano
Vemos que 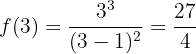 , assim, no ponto
, assim, no ponto  , a função tem um mínimo relativo.
, a função tem um mínimo relativo.
Exercícios para praticar
Encontre os máximos e mínimos das funções a seguir:
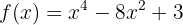
1Calculamos a primeira derivada da função e suas raízes.
Primeiro, a derivada da função:
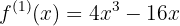
Agora, as raízes, resolvendo a equação:
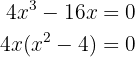
As raízes são:

2Calculamos a segunda derivada e verificamos o sinal que ela assume nas raízes.
A segunda derivada da função é:
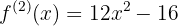
Avaliação das raízes na segunda derivada:
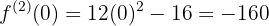 ,
,  em
em  a função tem um mínimo relativo.
a função tem um mínimo relativo.
 ,
,  em
em  a função tem um mínimo relativo.
a função tem um mínimo relativo.
3Calculamos a imagem (na função) dos extremos relativos.
 ,
,  em
em  o gráfico da função tem um mínimo relativo.
o gráfico da função tem um mínimo relativo.
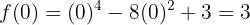 ,
, em
em 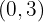 o gráfico da função tem um máximo relativo.
o gráfico da função tem um máximo relativo.
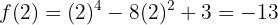 ,
,  em
em  o gráfico da função tem um mínimo relativo.
o gráfico da função tem um mínimo relativo.

1Calculamos a primeira derivada da função e suas raízes.
Primeiro, a derivada da função:
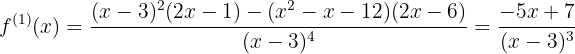
Agora, as raízes, resolvendo a equação:
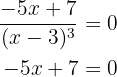
Portanto, a raiz é:
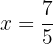
2Calculamos a segunda derivada e verificamos o sinal que ela assume na raiz.
A segunda derivada da função é:

Avaliação da raiz na segunda derivada:
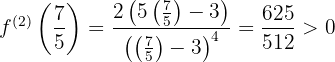 ,
,  em
em 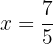 la função tem um mínimo relativo.
la função tem um mínimo relativo.
3Calculamos a imagem (na função) do extremo relativo.
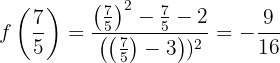
 em
em 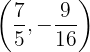 o gráfico da função tem um mínimo relativo.
o gráfico da função tem um mínimo relativo.
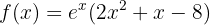
1Calculamos a primeira derivada da função e suas raízes.
Primeiro, a derivada da função:

Agora, as raízes, resolvendo a equação:
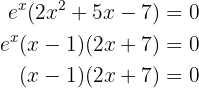
Significa que as raízes são:
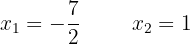
2Calculamos a segunda derivada e verificamos o sinal que ela assume nas raízes.
A segunda derivada da função é:
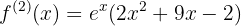
Vamos fazer a avaliação das raízes na segunda derivada:
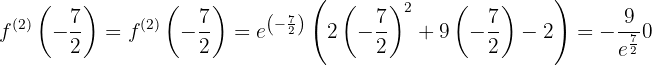 ,
,  e em
e em  a função tem um mínimo relativo.
a função tem um mínimo relativo.
3Calculamos a imagem (na função) dos extremos relativos.
 ,
,  em
em 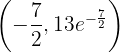 o gráfico da função tem um máximo relativo.
o gráfico da função tem um máximo relativo.
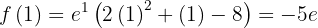 ,
,  em
em 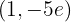 o gráfico da função tem um mínimo relativo.
o gráfico da função tem um mínimo relativo.
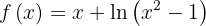
Neste caso é necessário considerar o domínio, pois pode ser que devamos descartar valores que não pertencem a ele.
Na verdade, sempre devemos analisar o domínio, mas às vezes é feito de forma implícita.
0Calculamos o domínio da função.
O domínio da função logaritmo natural é dado quando o argumento é positivo, então devemos resolver:
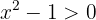
As soluções de 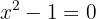 são
são 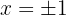 . Isso gera os intervalos
. Isso gera os intervalos 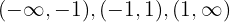 . Avaliando o sinal de
. Avaliando o sinal de 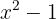 e conhecer o sinal gerado, para resolver:
e conhecer o sinal gerado, para resolver:
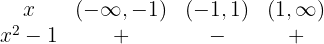
Portanto, o domínio da função é: 
1Calculamos a primeira derivada da função e suas raízes.
Primeiro, a derivada da função:
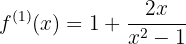
Agora, as raízes, resolvendo as equações:
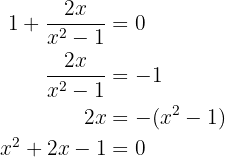
As raízes são:

Descartamos a 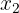 já que
já que 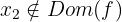
2Calculamos a segunda derivada e verificamos o sinal que ela assume nas raízes.
A segunda derivada da função é:
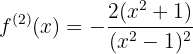
Vamos avaliar as raízes obtidas na segunda derivada:
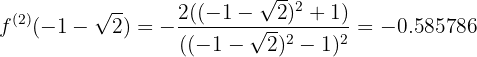 ,
, em
em  o gráfico da função tem um máximo relativo.
o gráfico da função tem um máximo relativo.

1Calculamos a primeira derivada da função e suas raízes.
Primeiro, a derivada da função:
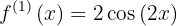
Agora, as raízes:
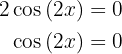
As raízes são:
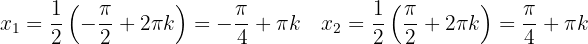 , com
, com 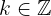
2Calculamos a segunda derivada e verificamos o sinal que ela assume nas raízes.
A segunda derivada da função é:

Vamos fazer a avaliação das raízes da segunda derivada:
 ,
,  em
em  a função tem um mínimo relativo para cada
a função tem um mínimo relativo para cada 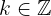
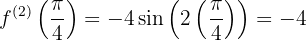 ,
,  em
em 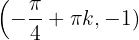 o gráfico da função tem um mínimo relativo para cada
o gráfico da função tem um mínimo relativo para cada 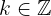
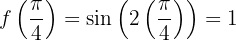 ,
,  em
em 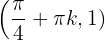 o gráfico da função tem um máximo relativo para cada
o gráfico da função tem um máximo relativo para cada 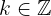
Problemas
Determine  ,
, e
e  para que a função
para que a função 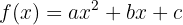 tenha um mínimo para
tenha um mínimo para  e assuma o valor
e assuma o valor 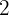 para
para  e
e 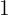 para
para  .
.
O problema se reduz a que ocorram as seguintes condições:
o que significa que devemos calcular a primeira derivada da função:
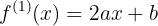
e, com isso, realizar as substituições:
obtendo-se um sistema de três equações com três incógnitas
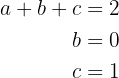
cuja solução é: 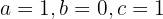
Determine  ,
, e
e  para que a função
para que a função 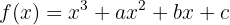 tenha um máximo para
tenha um máximo para 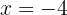 , um mínimo para
, um mínimo para  , e assuma o valor
, e assuma o valor 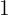 para
para  .
.
O problema se reduz a que ocorram as seguintes condições:
o que significa que devemos calcular a primeira derivada da função:

e, com isso, realizar as avaliações:
obtendo-se um sistema de três equações com três incógnitas:
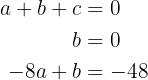
cuja solução é 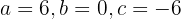
Determine o valor de  ,
, ,
, e
e 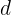 para que a função
para que a função 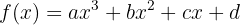 tenha um máximo em
tenha um máximo em  e um mínimo em
e um mínimo em 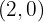 .
.
O problema se reduz a que ocorram as seguintes condições:
o que significa que devemos calcular a primeira derivada da função:

e, com isso, realizar as substituições correspondentes:
-
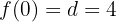
- latex]\displaystyle f(2)=8a+4b+2c+d=0[/latex]
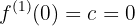
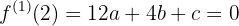
obtendo-se um sistema de quatro equações com quatro incógnitas
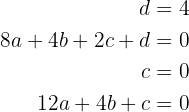
cuja solução é 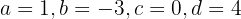
Considerando a função: 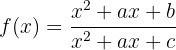
Calcule  ,
, e
e  , de modo que
, de modo que  tenha em
tenha em 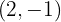 um extremo local e que a curva passe pela origem das coordenadas.
um extremo local e que a curva passe pela origem das coordenadas.
O problema se reduz a que ocorram as seguintes condições:
o que significa que devemos calcular a primeira derivada da função:
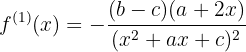
e, com isso, realizar as substituições:
obtendo-se um sistema de três equações com três incógnitas:
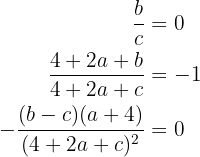
cuja solução é: 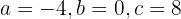
Encontre  e
e  para que a função:
para que a função: 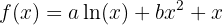 tenha extremos nos pontos
tenha extremos nos pontos 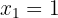 e
e 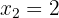 . Para esses valores de
. Para esses valores de  e
e  , qual tipo de extremos tem a função a função em
, qual tipo de extremos tem a função a função em 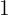 e em
e em 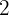 ?
?
Vamos calcular a primeira e a segunda derivada da função, isto é, para buscar as condições para que haja extremos e depois para conhecer sua natureza.
Agora, como queremos que a função tenha extremos nos pontos 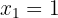 e
e 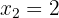 , estabelecem-se as seguintes igualdades:
, estabelecem-se as seguintes igualdades:
gerando um sistema cuja solução é: e
e 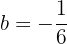 .
.
Já encontramos os valores que fazem a função ter extremos nos pontos indicados; agora vejamos sua natureza. Para isso precisamos da segunda derivada da função:

Agora vejamos a natureza de cada extremo:
-
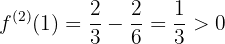 ,
,  em
em 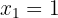 , a função tem um mínimo relativo.
, a função tem um mínimo relativo.
-
-
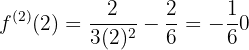 ,
,  em
em 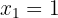 , a função tem um mínimo relativo.
, a função tem um mínimo relativo.
-
Resumir com IA: