Temas
Definição
A função exponencial é aquela em que a cada valor real 
indicamos a potência 
com 
e 
. Esta função é expressada com
o número 
denomina-se base.
Gráficos de funções exponenciais
Analisemos o comportamento da função exponencial de acordo com sua base
Construímos uma tabela de valores para 
| X | f(x) |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
Traçamos o gráfico
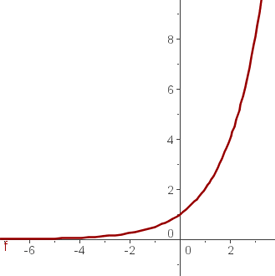
Agora construímos uma tabela de valores para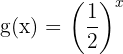 
|  |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
Traçamos o gráfico
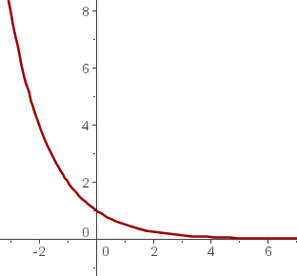
Podemos observar que a primeira função é estritamente crescente, enquanto que a segunda é estritamente decrescente; além disso, ambas são simétricas em relação ao eixo 
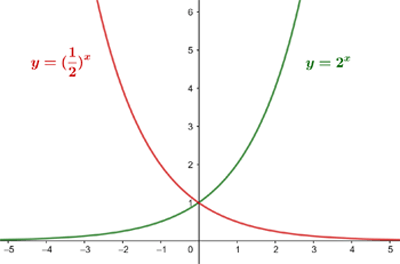
Função exponencial natural
Está indicada por 
onde 
está dado por
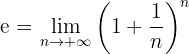
Esta notação foi introduzida por Leonhard Euler por volta de 1730, quando descobriu muitas propriedades deste número. O número é irracional e suas primeiras dez cifras decimais são 
.
Propriedades da função exponencial
1 Domínio: 
.
2 Campo: 
.
3 É contínua.
4Os pontos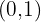 
e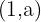 
pertencem ao gráfico.
5 É injetiva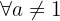 
(nenhuma imagem tem mais de um original).
6 Crescente se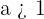 
.
7 Decrescente se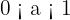 
.
8 As curvas e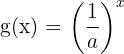 
são simétricas em relação ao eixo .
9 A função exponencial , com 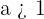eventualmente cresce mais rápido do que a função potência 
para qualquer 
.
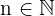10 A função inversa da função exponencial é 
. A função inversa da exponencial natural é 
.
Aplicações da função exponencial
As funções exponenciais são usadas para modelar uma ampla variedade de fenômenos como o crescimento de populações e taxas de juros.
Crescimento e decaimento exponencial
A fórmula usada para modelar o crescimento de uma população está dada por
A função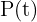 
cresce exponencialmente e representa a quantidade de uma população com tempo 
; 
representa a constante de crescimento ou decaimento; se 
chamaremos de constante de crescimento, enquanto que se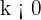 
chamaremos de constante de decaimento. 
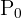representa a população inicial com tempo zero, isto é, 
.
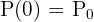A fórmula anterior se encontra expressada na função de exponencial natural, mas em algumas ocasiões se expressa com base , isto é fácil de obter, basta aplicar as propriedades dos expoentes com 
e considerar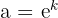 
para obter
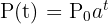
Exemplo: Um grupo de pesquisadores estuda um cultivo de bactérias. Se no início da observação há 
bactérias e meia hora depois há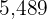 
, encontre:
1 A quantidade de bactérias ao final de duas horas.
2 A quantidade de bactérias ao final de três horas.
3 A taxa média de mudança da população durante a segunda hora.
4 O tempo necessário para duplicar a população inicial.
5 Quando esta população atingirá um número de 
?
Para poder responder, primeiro precisamos conhecer na fórmula de crescimento populacional com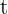 
expressado em minutos.
Podemos notar que conhecemos a população inicial 
, mas nos falta ainda o valor da constante de crescimento. Para encontrar o valor de 
utilizamos os dados do problema: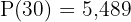 
na fórmula de crescimento
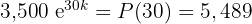
Dividindo ambos os dados por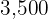 
e aplicando a função inversa do exponencial natural, obtemos
Assim, a função que modela o crescimento da população de bactéria é
1 A quantidade de bactérias ao final de duas horas é
2 A quantidade de bactérias ao final de três horas é
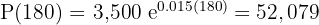
3 A taxa média de mudança da população durante a segunda hora
Durante a segunda hora, o tempo de 
a 
, a população mudou para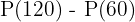 
, de modo que a taxa média nesse período de tempo é
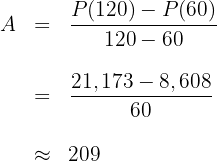
A população aumenta à uma taxa média aproximada de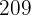 
bactérias por minuto durante a segunda hora.
4 O tempo requerido para duplicar a população inicial
Para descobrir usamos a seguinte igualdade
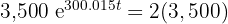
Dividindo ambos os lados por 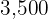e aplicando a função inversa do exponencial natural, obtemos
Assim, o tempo necessário para que a população de bactérias duplique é de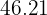 
minutos.
5 Quando esta população atingirá um número de ?
Para descobrir usamos a seguinte igualdade
Dividindo ambos os lados por 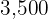e aplicando a função inversa do exponencial natural, obtemos
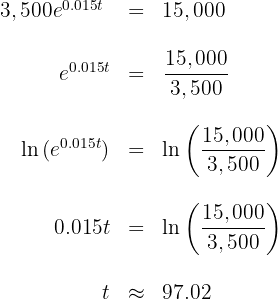
Assim, o tempo necessário para que a população de bactérias seja 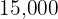de 
é de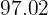 
minutos.
Juros composto
Uma quantidade inicial de dinheiro é investida 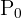à uma taxa de juros 
expressada em decimais. Se o juros é capitalizado de uma só vez, então o valor que será obtido 
depois de somar o juros é
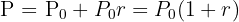
Se o juros é capitalizado mais de uma vez, o juros somado na conta durante um período, acumulará juros durante os períodos seguintes. Se a taxa anual de juros é e o juros é capitalizado 
vezes por ano, então ao final de anos, o juros foi capitalizado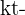 
vezes e o saldo chamado valor futuro é
Exemplo: São investidos 
à uma taxa de 
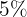anual. Encontre o valor futuro de 
anos sabendo que o juros é composto trimestralmente.
Para encontrar o valor futuro depois de anos se o juros é capitalizado trimestralmente, usamos 
.
Substituímos os valores na fórmula do valor futuro
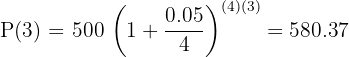
O saldo obtido depois de anos é de 
Juros composto continuamente
Para saber o saldo de um investimento ao final de anos quando a frequência de capitalização é incrementada sem limite, isto é, o juros não é capitalizado trimestralmente, nem mensualmente, nem diariamente, mas continuamente, usamos a fórmula
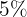Exemplo: São investidos à uma taxa de anual. Encontre o valor futuro de anos sabendo que o juros é composto continuamente.
Para encontrar o valor futuro depois de anos sabendo que o juros é capitalizado continuamente, usamos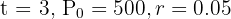 
.
Substituímos os valores na fórmula do valor futuro
O saldo obtido depois de anos é de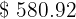 
e é o limite superior para o saldo possível.
Gostou desse artigo? Deixe uma nota!
Loading...
