Temas
Definição de logaritmo
O logaritmo de um número, em uma base dada, é o expoente ao qual a base deve ser elevada para se obter esse número.
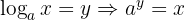a > 0, 
Sendo 
a base, 
o número e 
o logaritmo.
Logaritmos decimais e logaritmos naturais
Os logaritmos decimais têm base 
. São representados por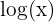 
Os logaritmos naturais (também chamados de neperianos ) têm base 
. São representandos por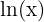 
ou 
.
Exemplos de uso da definição de logaritmo
Escreva os seguintes logaritmos na forma exponencial:
1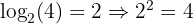 
2 
3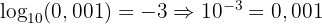 
4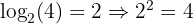
Usando a definição de logaritmo e álgebra, calcule o valor da incógnita nas equações a seguir:
1. 
Aplicamos a definição de logaritmo e reescrevemos 
como fração decimal simplificada:
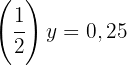
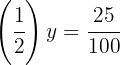
Agora representamos 
como potência e igualamos os expoentes:
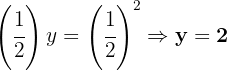
2. 
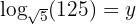
Aplicamos a definição de logaritmo, escrevendo a raiz como potência com expoente fracionário:
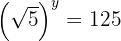
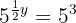
Igualamos os exponentes:
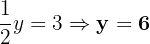
3. 
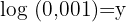
Aplicamos a definição de logaritmo e reescrevemos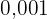 
como fração decimal:
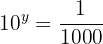
Agora representamos a fração como potência de base e igualamos os exponentes:
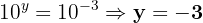
4. 
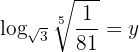
Aplicamos a definição de logaritmo, reescrevemos as raízes como potências e igualamos os expoentes:
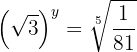
.5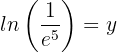 
Aplicamos a definição de logaritmo, lembrando que a base do logaritmo natural é .
Escrevemos a fração como potência e igualamos os expoentes:
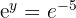
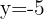
Propriedades dos logaritmos
1 O logaritmo de um produto é igual à soma dos logaritmos dos fatores:
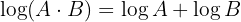
2 O logaritmo de um quociente é igual à diferença entre o logaritmo do dividendo e o logaritmo do divisor:
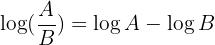
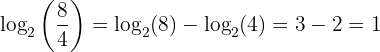
3 O logaritmo de uma potência é igual ao produto do expoente pelo logaritmo da base:
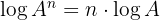
4 O logaritmo de uma raiz é igual ao quociente entre o logaritmo do radicando e o índice da raiz:
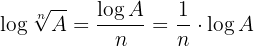
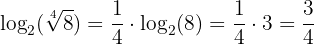
Das propriedades 
e 
podemos deduzir que:
5 O logaritmo de um número na sua própria base '' de '' é 
.
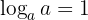
6 O logaritmo de é 
(independentemente da base):
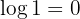
Portanto:
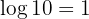
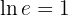
7 O argumento de um logaritmo sempre deve ser maior que zero:
Para 
é necessário que x> 0
Função logarítmica
A função logarítmica de base é a função inversa da função exponencial de base .
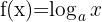
a > 0,
Exemplos de funções logarítmicas
|  |
|---|---|
 |  |
 |  |
 |  |
| |
 | |
| |
 | |
|  |
|---|---|
 | |
| |
| |
| |
| |
| |
| |
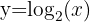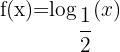
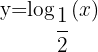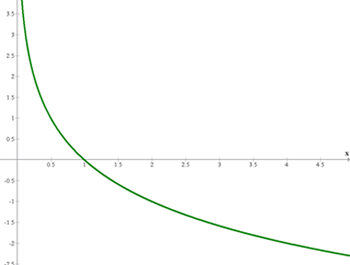
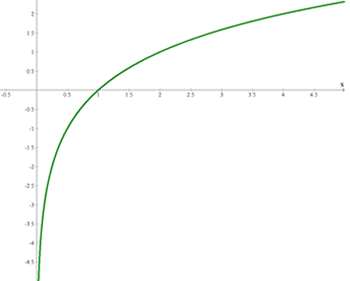
As propriedades das funções logarítmicas
- Domínio:
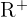
- Contradomínio
- A função é contínua.
- Os pontos
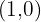e 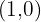pertencem ao gráfico. - A função é injetora (nenhuma imagem tem mais de um valor original).
- Crescente quando a > 1
- Decrescente quando 0<a<1
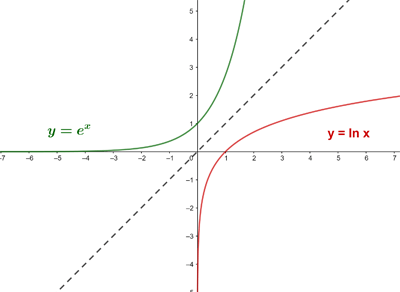
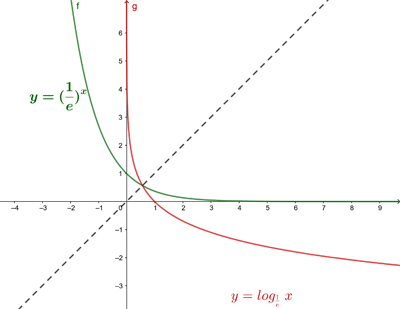
O gráfico da função logarítmica é simétrico em relação à bissetriz do primeiro e do terceiro quadrante, pois é a função inversa da função exponencial (ou função recíproca).
a>1
0<a<1
Gostou desse artigo? Deixe uma nota!
Loading...
