Temas
Às vezes, encontramos funções que apresentam uma indeterminação do tipo infinito dividido por infinito. Ou seja, considere a função:
de forma que 
y 
.
Assim, ao avaliar essa função em
obtemos:
Nesse caso, dizemos que a função está indeterminada em , pois não é possível atribuir um valor definido a 
. No entanto, podemos usar dois métodos diferentes para encontrar o limite da função em , lembrando que o limite em não o mesmo que o valor de —:
Primeiro método: comparação do grau dos polinômios
Esse método funciona apenas para funções racionais da forma:
em que 
e 
ão polinômios, além de alguns casos especiais envolvendo exponenciais e radicais. Quando não estamos nesses casos, utilizamos outros métodos, como a Regra de L’Hôpital.
O método consiste em comparar os graus de e :
O numerador tem grau maior que o denominador
Quando tem o grau maior que o denominador, então o limite será 
ou 
.
O sinal do limite será o mesmo do quociente entre os coeficientes dos termos de maior grau.
No segundo exemplo abaixo, o limite é pois o quociente é 
; ou seja, tem sinal negativo.
O grau do denominador é maior que o do numerador
Quando tem grau maior, então o limite sempre será 0.
Numerador e denominador têm o mesmo grau
Se o numerador e o denominador têm o mesmo grau, então o limite é o quociente entre os coeficientes de maior grau. Observemos o exemplo abaixo. O numerador tem coeficiente principal 2, enquanto o denominador tem coeficiente principal 3. Portanto, como ambos os polinômios têm o mesmo grau, o limite é 
.
Casos particulares do método de comparação
Considerando uma função:
existem casos em que podemos comparar a 
e 
de maneira semelhante ao que fazemos com polinômios. Esses casos envolvem funções exponenciais e funções radicais.
1 Se ou forem exponenciais, então podemos considerar que seu grau é sempre maior que o de qualquer polinômio (formalmente, dizemos que uma função exponencial é de ordem superior a um polinômio).
Se tanto o numerador quanto o denominador forem exponenciais, terá maior ordem aquela cuja base for maior.
2 Se o numerador ou o denominador é um radical da forma
,
então consideramos que seu grau é 
e seu coeficiente dominante é 
.
Segundo método: dividir numerador e denominador por uma mesma função
Considerando que
podemos multiplicar e dividir a função por para calcular o limite de forma mais simples. Isso porque:
Quociente de polinômios
Se estivermos lidando com o quociente de polinômios, dividimos ambos pelo termo de maior grau. Por exemplo:
Dividimos cada polinômio por 
, simplificamos as frações e aplicamos o limite:
É importante observar o sinal dos coeficientes principais do numerador e do denominador, pois isso determina o sinal do infinito. Assim como no método anterior, o sinal do limite será o mesmo que o do quociente desses coeficientes.
Funções exponenciais
Se forem funções exponenciais, dividimos pela exponencial de maior base. Observe o exemplo:
Primeiro aplicamos propriedades de potências para eliminar somas ou subtrações nos expoentes:
Dividimos o numerador e o denominador por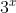 
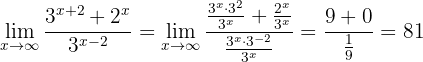
Exemplos da indeterminação infinito dividido por infinito
Vamos resolver alguns exemplos para aplicar o que vimos:
1 
O resultado é: 
porque o numerador é de ordem maior que o denominador.
2
Aqui o denominador é de ordem superior. Portanto, o limite é 0.
3
Temos um radical no numerador, cujo grau consideramos 
. Como 4 > 7/2, o limite é 0.
4
Como comentado antes, funções exponenciais sempre têm ordem maior que polinômios, mesmo que o polinômio seja de grau 23. Portanto, o limite é .
Gostou desse artigo? Deixe uma nota!
Loading...
