Temas
Dados dois conjuntos 
e 
, chamamos de função a correspondência de na qual todos os elementos de têm no máximo uma imagem em , isto é, uma imagem ou nenhuma.
Uma função real de variável real é toda correspondência 
que associa a cada elemento de um determinado subconjunto dos números reais, chamado domínio, outro número real.
O subconjunto no qual a função se define é chamado de domínio ou campo de existência da função e é indicado por 
.
O número 
pertencente ao domínio da função, recebe o nome de variável independente.
O número, 
, associado por ao valor chama-se variável dependente. A imagem de é designada por 
. Assim:
O conjunto dos valores reais que a variável ou pode assumir é chamado de imagem ou contradomínio da função.
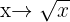
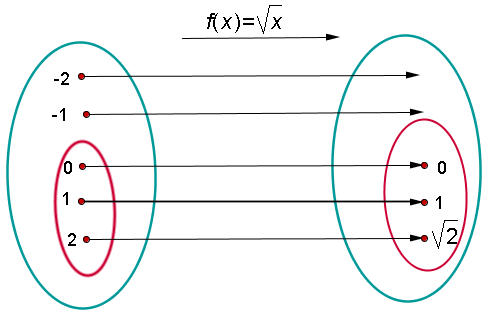
Conjunto inicial Conjunto final
Domínio Conjunto imagem ou contradomínio
O domínio é o conjunto de elementos que têm imagem:
A imagem (ou contradomínio efetivo) é o conjunto dos elementos que são imagens:
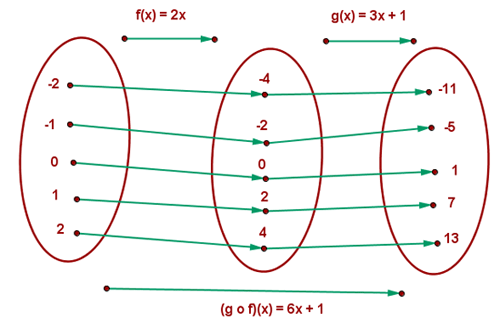
Composição de funções
Se temos duas funções: e 
, de modo que o domínio de uma esteja contido na imagem da outra, pode-se definir uma nova função que associa a cada elemento do domínio de o valor de 
.
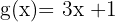
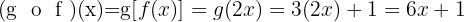
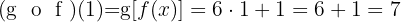
Domínio
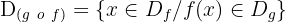
Propriedades
1 Associatividade
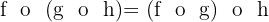
2 Não comutativa
3 Elemento neutro: a função identidade,
.
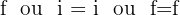
Exemplos de composição de funções
Considerando as funções:
1
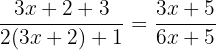
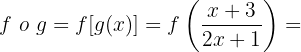
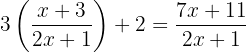
2
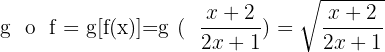
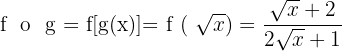
3
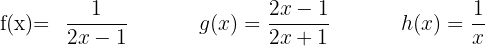
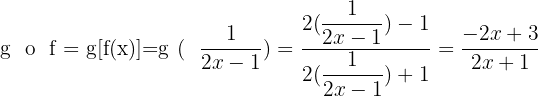
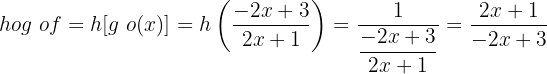
Função inversa ou recíproca
Chama-se função inversa ou recíproca de a outra função 
que satisfaça:
Se 
, então 
.
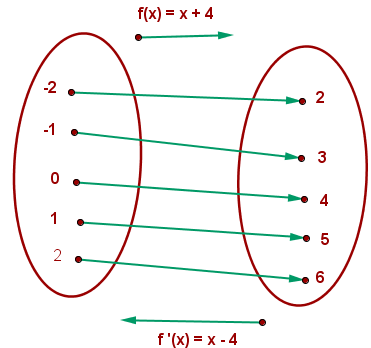
Podemos observar que:
O domínio de é a imagem de .
A imagem de é o domínio de .
Se queremos encontrar a imagem de uma função temos que encontrar o domínio de sua função inversa.
Se duas funções são inversas, sua composição é a função identidade.
Os gráficos de e são simétricos em relação à bissetriz do primeiro e terceiro quadrante.
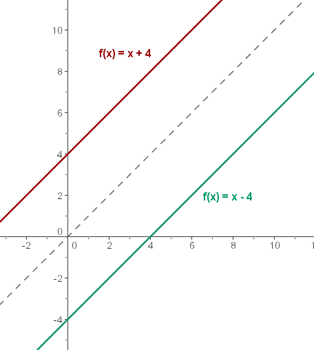
É importante distinguir entre a função inversa 
e a função recíproca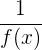 
.
Passos para o cálculo da função inversa
1 Escreve-se a equação da função em e .
2 Isola-se a variável em função de .
3 Trocam-se as variáveis.
Exemplos de cálculo da inversa
1
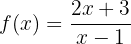
Primeiro, escrevemos a equação da função e .
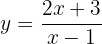
Fazemos as operações:
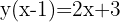
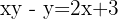
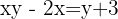
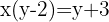
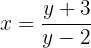
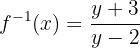
Fazemos a verificação:
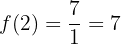
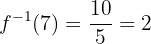
2
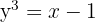
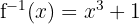
3
Neste caso, não é uma função.
Gostou desse artigo? Deixe uma nota!
Loading...
