Função quadrática
As funções polinomiais são aquelas formadas por um polinômio. Um exemplo desse tipo é a função quadrática ou de segundo grau, representada graficamente por uma parábola e pela seguinte equação:
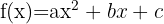
Representação gráfica da parábola
Para construir o gráfico de uma parábola, é necessário conhecer os seguintes elementos:
Vértice
Pelo vértice passa o eixo de simetria da parábola. Ou seja, quando o coeficiente do termo 
é positivo, o vértice será o ponto mais baixo do gráfico. As fórmulas para encontrá-lo são:
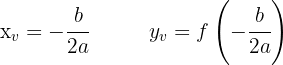
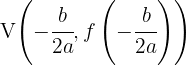
A equação do eixo de simetria é:
Pontos de interseção com o eixo X
Para encontrar o valor de 
quando 
devemos igualar a segunda coordenada a zero, ou seja, resolver a seguinte equação:
Ao resolver essa equação, podemos encontrar os seguintes casos:
-
- Dois pontos de interseção:
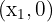e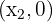 
isso ocorre se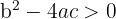 
- Um ponto de interseção: 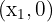isso ocorre se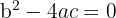
- Nenhum ponto de interseção: isso ocorre se
- Dois pontos de interseção:
Ponto de interseção com o eixo Y
Para encontrar a interseção com o eixo 
basta igualar a primeira coordenada a zero, ou seja, 
. Assim, temos:
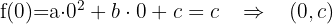
Exemplo
Para representar a função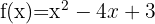 
, é necessário encontrar os seguintes elementos que compõem a parábola:
Vértice
Aplicamos as fórmulas descritas anteriormente para encontrar as coordenadas do vértice:
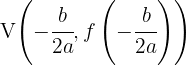
Portanto, as coordenadas do vértice são: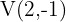 
Pontos de interseção com o eixo X
Para encontrar o ponto ou os pontos de interseção com o eixo X, igualamos a função a zero, conforme indicado anteriormente:
Para resolver a equação, utilizamos a fórmula de Bhaskara para:
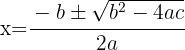
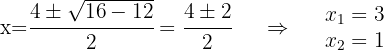
Neste caso, encontramos dois pontos de interseção: 
y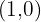 
Ponto de interseção com o eixo Y
Para encontrar o ponto de interseção com o eixo , basta observar o valor da constante 
que neste caso é 
e resultando nas coordenadas: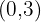
.
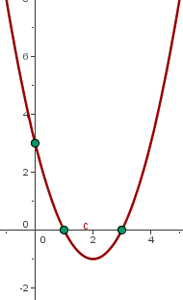
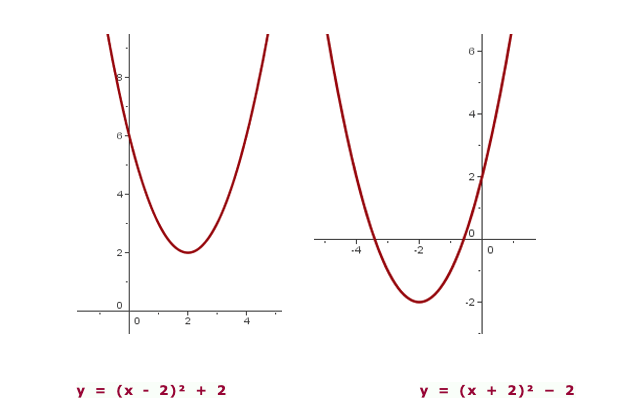
Gráfico da função quadrática
Começamos pela função de 
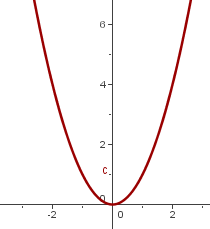
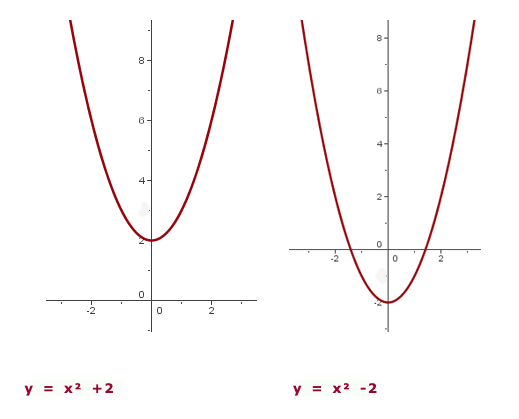
Traslação vertical
Se a função for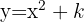 
Onde:
- k > 0, então é deslocada para cima
unidades. - k < 0, entonces é deslocada para baixo unidades.
Nesse caso, o vértice da parábola é: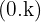 
.
E o eixo de simetria é: .
Traslação horizontal
Para a equação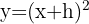 
Onde:
- Se, h < 0 , então é deslocada para a esquerda
unidades. - Se, h < 0 , entonces é deslocada para a direita unidades.
Nesse caso, o vértice da parábola é: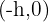 
.
E o eixo de simetria é: 
.
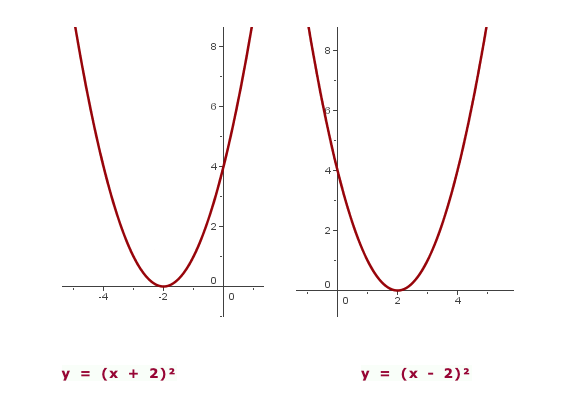
Translação oblíqua
Por fim, na seguinte expressão 
, o vértice da parábola é: 
.
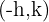E o eixo de simetria: .
Gostou desse artigo? Deixe uma nota!
Loading...
