Temas

O que é infinito e como resolvemos exercícios de limites
Quando resolvemos limites, com frequência precisamos operar com o infinito. No entanto, devemos lembrar que o infinito não é um número. Em algumas ocasiões vamos operá-lo com um número com o propósito de encontrar limites, porém, devemos levar em consideração que em muitas ocasiões o infinito não se comporta como um número.
Existem algumas ocasiões onde a operação com o infinito está indeterminada. Esta é uma das ocasiões onde  não se comporta como um número. Quando nos deparamos com algumas dessas operações indeterminadas, devemos fazer uma pequena modificação na função da qual estamos calculando o limite, com o propósito de evitar a indeterminação. Isso é conhecido como “evitar a indeterminação”.
não se comporta como um número. Quando nos deparamos com algumas dessas operações indeterminadas, devemos fazer uma pequena modificação na função da qual estamos calculando o limite, com o propósito de evitar a indeterminação. Isso é conhecido como “evitar a indeterminação”.
A definição épsilon-delta do limite é a seguinte:
Um valor  é o limite da função
é o limite da função  no
no  se para todo
se para todo 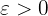 existe um
existe um 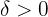 tal qual para todo
tal qual para todo  que satisfaz
que satisfaz 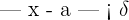 cumpre-se
cumpre-se 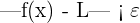 .
.
Considere que quando os critérios da definição são cumpridos, esta é uma forma de demonstrar que existe o limite para uma função em  .
.
Exercícios com definição de limite
Utilizando a definição de limite (épsilon-delta), prove que
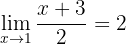
Consideramos 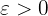 arbitrário. Devemos provar que existe um
arbitrário. Devemos provar que existe um 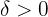 que satisfaça a definição de limite.
que satisfaça a definição de limite.
Desejamos que, quando 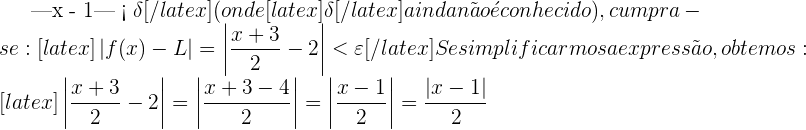
Queremos deixar 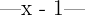 isolado para obter uma fórmula para
isolado para obter uma fórmula para 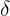 . Multiplicando ambos os lados da desigualdade por 2, temos:
. Multiplicando ambos os lados da desigualdade por 2, temos: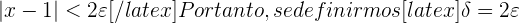 , a desigualdade será satisfeita. Assim, a demonstração está concluída.
, a desigualdade será satisfeita. Assim, a demonstração está concluída.
O que isso significa?
Significa que, para qualquer 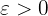 dado, podemos encontrar um
dado, podemos encontrar um 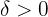 que satisfaça a definição de limite, já que temos a fórmula
que satisfaça a definição de limite, já que temos a fórmula 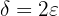 .
.
Exemplo numérico
Se 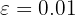 , então:
, então: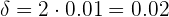
Portanto, se 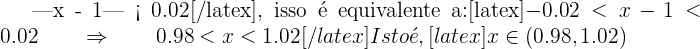 .
.
Para qualquer  neste intervalo, cumpre-se
neste intervalo, cumpre-se 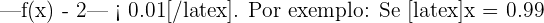 , então
, então 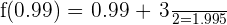 , e:
, e: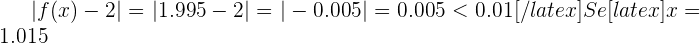 , então
, então 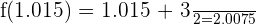 , e:
, e: \displaystyle |f(x) - 2| = |2.0075 - 2| = |0.0075| = 0.0075 < 0.01[/latex]
\displaystyle |f(x) - 2| = |2.0075 - 2| = |0.0075| = 0.0075 < 0.01[/latex]
Dessa forma, a demonstração e os exemplos mostram que a definição de limite é satisfeita.
Limites a partir do gráfico de uma função
Observe o seguinte gráfico de  e determine os limites pedidos:
e determine os limites pedidos:
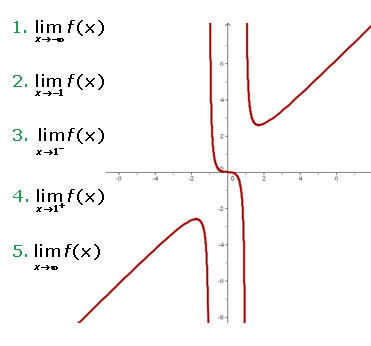
1) No primeiro limite é pedido que
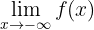
Podemos notar que quando 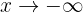 , isto é, quando
, isto é, quando  decresce “infinitamente”, a função também decresce infinitamente. Portanto,
decresce “infinitamente”, a função também decresce infinitamente. Portanto,
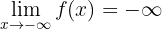
2) Agora é pedido que seja determinado
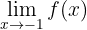
Neste caso, podemos observar que quando  se aproxima muito de
se aproxima muito de  pela esquerda, a função decresce infinitamente. Por outro lado, quando
pela esquerda, a função decresce infinitamente. Por outro lado, quando  se aproxima muito de
se aproxima muito de  pela direita, a função cresce infinitamente. Portanto, podemos concluir que o limite não existe.
pela direita, a função cresce infinitamente. Portanto, podemos concluir que o limite não existe.
3) Agora é pedido para calcular
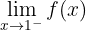
referente ao limite pela esquerda. Podemos observar que, quando  se aproxima de
se aproxima de  pela esquerda, a função decresce infinitamente. Portanto, o limite é
pela esquerda, a função decresce infinitamente. Portanto, o limite é
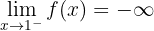
4) O quarto limite é

que se trata agora do limite pela direita. Portanto,
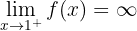
5) Por último, é pedido o limite

do qual é muito similar ao primeiro limite. Podemos observar que  cresce indefinidamente,
cresce indefinidamente,  também cresce indefinidamente. Portanto,
também cresce indefinidamente. Portanto,
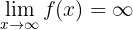
Cálculo de limites
Calcule o limite:

Desejamos encontrar o limite
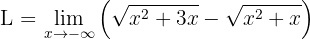
Devemos notar primeiro que se “calculamos no infinito”, obteremos uma forma indeterminada:
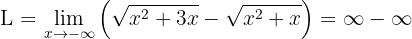
Como o valor de  não está determinado, precisamos fazer uma manipulação algébrica da nossa função.
não está determinado, precisamos fazer uma manipulação algébrica da nossa função.
Antes de fazer uma manipulação algébrica, vamos transformar o limite utilizando a propriedade:
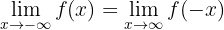
Assim, o limite é:
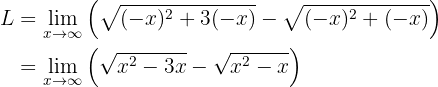
Agora precisamos manipular algebricamente os limites com o propósito de acabar com a subtração de infinitos. Isto é feito “racionalizando” (isto é, multiplicando e dividindo pelo conjugado):
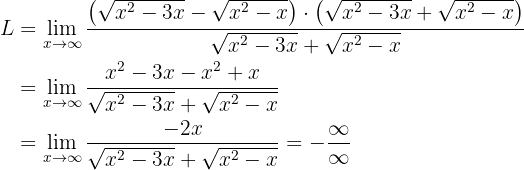
Podemos observar que se calcularmos o infinito, voltaremos a ter uma nova indeterminação. Neste caso trata-se de uma indeterminação 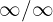 . Para acabar com esta indeterminação devemos fazer outra manipulação algébrica. Neste caso, devemos multiplicar e dividir por
. Para acabar com esta indeterminação devemos fazer outra manipulação algébrica. Neste caso, devemos multiplicar e dividir por 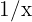 :
:
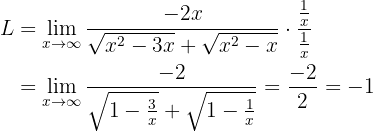
Que é o resultado que estávamos buscando.
Calcule o seguinte limite:
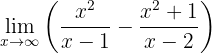
Agora temos o limite:

Podemos notar que se calculamos no infinito diretamente, obteremos:
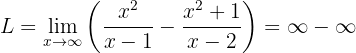
Para acabar com esta indeterminação podemos somar as frações (utilizando o denominador comum)
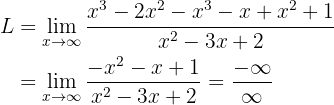
Como agora temos uma indeterminação da forma 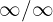 , então devemos multiplicar e dividir por um termo apropriado para evitar a indeterminação. O termo apropriado é o monômio de maior grau no numerador ou denominador, isto é,
, então devemos multiplicar e dividir por um termo apropriado para evitar a indeterminação. O termo apropriado é o monômio de maior grau no numerador ou denominador, isto é, 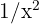 . Portanto, fica assim:
. Portanto, fica assim:
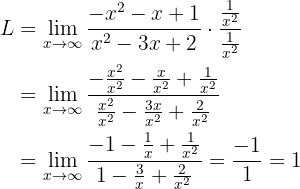
Assim, o limite é  .
.
Calcule o seguinte limite:

Se calculamos no infinito, obteremos o seguinte:
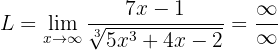
Da qual é uma indeterminação de 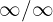 . Portanto, devemos multiplicar e dividir entre o monômio de maior grau (seja em numerador ou denominador). Neste caso é
. Portanto, devemos multiplicar e dividir entre o monômio de maior grau (seja em numerador ou denominador). Neste caso é 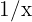 —como o denominador implica uma raiz cúbica, então o “monômio”
—como o denominador implica uma raiz cúbica, então o “monômio”  é considerado como um monômio de grau 1—. Assim:
é considerado como um monômio de grau 1—. Assim:
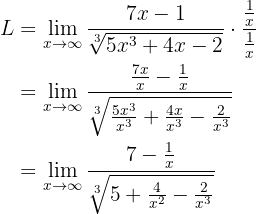
Que ao “calcular no infinito”, temos:

Calcule o seguinte limite:
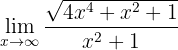
Se calculamos a função no infinito, obteremos:

Portanto, por ser uma forma indeterminada, devemos multiplicar e dividir pelo monômio de maior grau ( ; vale lembrar que as potências do numerador devem ser divididas por 2 já que se encontram dentro de uma raiz quadrada):
; vale lembrar que as potências do numerador devem ser divididas por 2 já que se encontram dentro de uma raiz quadrada):
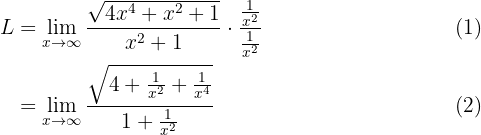
Assim, calculando no infinito, temos:
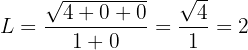
Portanto, o limite é 2.
Calcule o seguinte limite:
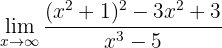
Se calculamos a função no infinito, de imediato podemos notar que:
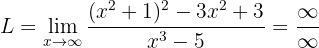
Portanto, devemos fazer uma manipulação algébrica para poder acabar com a indeterminação.
Este limite podemos resolver de duas maneiras.
1) Com a comparação de infinitos:
Primeiro devemos expandir o binômio ao quadrado, assim obtemos

Devemos notar que no numerador obtemos  enquanto que no denominador obtemos
enquanto que no denominador obtemos  como termos de maior grau. Assim, o grau do numerador é maior e o limite será
como termos de maior grau. Assim, o grau do numerador é maior e o limite será  . Recordemos que quando o grau do numerador é maior, então o limite é
. Recordemos que quando o grau do numerador é maior, então o limite é  caso os termos de maior grau tenham o mesmo sinal.
caso os termos de maior grau tenham o mesmo sinal.
2) Dividindo numerador e denominador pelo termo de maior grau:
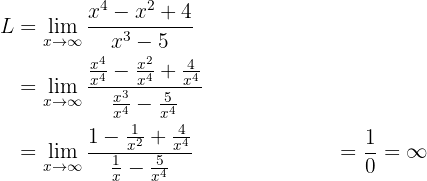
Podemos observar que, de maneira geral,  é uma forma indeterminada. No entanto, estamos calculando um limite quando
é uma forma indeterminada. No entanto, estamos calculando um limite quando  , além disso, tanto o numerador como o denominador são positivos conforme
, além disso, tanto o numerador como o denominador são positivos conforme  cresce. Portanto, podemos concluir que o limite será
cresce. Portanto, podemos concluir que o limite será  .
.
Calcule o seguinte limite:

Se calculamos no infinito, temos:

No entanto, o infinito do denominador tem uma ordem superior. Portanto, podemos concluir que 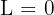 .
.
Não obstante, demonstra que o limite é 0 sem utilizar o critério de “ordem” é complicado. Para fazer, expressamos:
Para encontrar o limite, devemos procurar duas funções  e
e  tais como
tais como  e
e

Se encontrarmos estas funções, então podemos concluir que 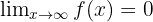 .
.
Em primeiro lugar, devemos observar que quando 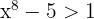 , então
, então 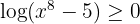 (e isso cumpre-se quando
(e isso cumpre-se quando  é grande). De qualquer forma, sabemos que
é grande). De qualquer forma, sabemos que  para
para 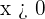 . Portanto:
. Portanto:
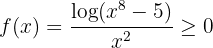
quando  "é suficientemente grande". Assim, sabemos que
"é suficientemente grande". Assim, sabemos que 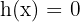 onde está claro que
onde está claro que 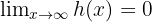 .
.
Para encontrar a segunda função, primeiro devemos notar que 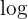 é uma função crescente, portanto, já que
é uma função crescente, portanto, já que  , então
, então  . Assim, temos
. Assim, temos
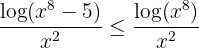
agora, se pegarmos  , então podemos escrever
, então podemos escrever
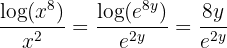
Uma propriedade muito importante sobre a função exponencial é
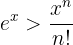
para qualquer  y
y 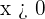 . Se pegarmos
. Se pegarmos 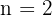 , então teremos
, então teremos

Prosseguimos
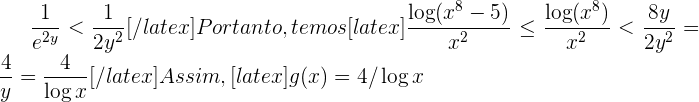 onde
onde  . Além disso,
. Além disso,  h(x) \leq f(x) < g(x)[/latex]. Portanto, [latex]\lim_{x \to \infty}{f(x)} = 0[/latex].
h(x) \leq f(x) < g(x)[/latex]. Portanto, [latex]\lim_{x \to \infty}{f(x)} = 0[/latex].
Calcule o seguinte limite:
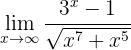
Se calculamos no  , então obteremos
, então obteremos
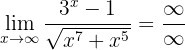
Aqui também podemos observar a “ordem” do denominador e numerador para determinar o limite. Neste caso o numerador tem um limite de ordem superior, portanto,
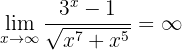
Para demonstrar, vamos expressar
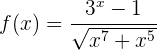
e devemos encontrar uma função  tal como
tal como 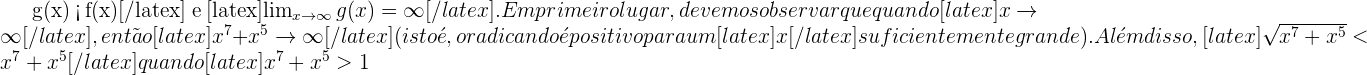 , portanto
, portanto
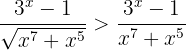
Agora podemos notar que se  , então
, então 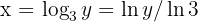 . Daqui prosseguimos
. Daqui prosseguimos

Portanto, 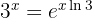 . De qualquer forma, como sabemos que
. De qualquer forma, como sabemos que
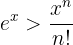
quando 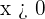 , então temos
, então temos
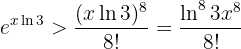
Assim
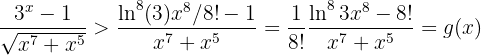
onde 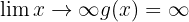 . Portanto, o limite é
. Portanto, o limite é
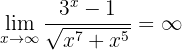
Calcule o seguinte limite:
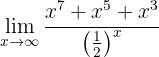
Ao calcular no infinito, temos

Portanto, o limite deve ser infinito, pois tanto o numerador como o denominador são positivos para um  suficientemente grande. Para poder ver de forma mais clara, observe que
suficientemente grande. Para poder ver de forma mais clara, observe que
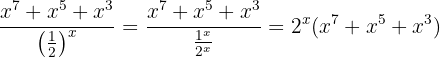
Portanto,
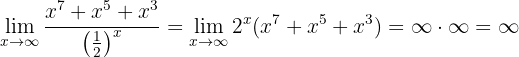
Calcule o seguinte limite:
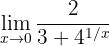
Se calculamos no 0, temos

onde temos uma forma indeterminada da forma  . Devemos notar que neste caso não podemos dizer que
. Devemos notar que neste caso não podemos dizer que  já que estamos calculando um limite quando
já que estamos calculando um limite quando 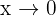 e
e  é positivo ou negativo próximo do 0 (quando calculamos limites
é positivo ou negativo próximo do 0 (quando calculamos limites  isso geralmente não é um problema).
isso geralmente não é um problema).
Portanto, devemos calcular os limites laterais:
1) Primeiro calculamos o limite pela esquerda
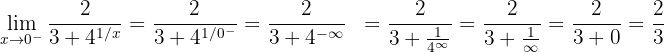
2) Agora calculamos o limite pela direita
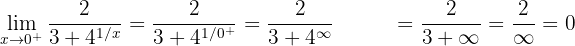
Aqui podemos observar que os dois limites laterais são diferentes, portanto, o limite quando 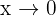 não existe.
não existe.
Calcule o seguinte limite:
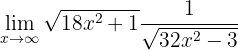
Se “calculamos no infinito”, obtemos

Portanto, devemos fazer uma manipulação algébrica. Primeiro devemos escrever o limite como uma só fração:
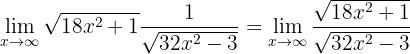
Agora dividimos o numerador e o denominador pelo coeficiente de maior grau (isto é  já que encontra-se dentro de uma raiz):
já que encontra-se dentro de uma raiz):
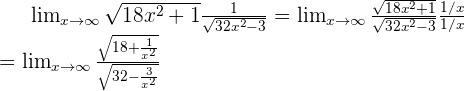
Agora já podemos calcular no infinito, de modo que obteremos:
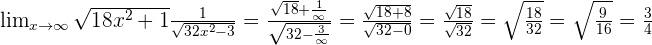
Portanto, o limite é 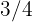 .
.
Encontre o seguinte limite:
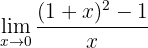
Se calculamos no 0, podemos observar que
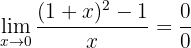
assim temos uma indeterminação e precisamos fazer uma manipulação algébrica. Para isso, expandimos o binômio ao quadrado:
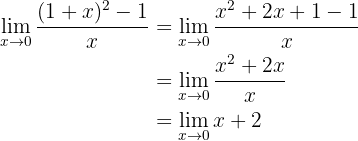
Se calculamos agora no 0, obteremos:
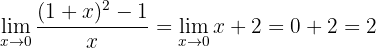
Portanto, o limite é 2.
Calcule o seguinte limite:

Se calculamos com 3, obteremos
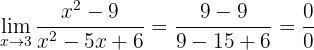
Assim, podemos observar que temos, de novo, uma forma indeterminada. Para evitar a indeterminação fatoramos tanto o numerador como o denominador (observe que o numerador é uma diferença de quadrados; enquanto que o denominador pode ser fatorado quando encontramos números que quando multiplicados deem 6 e que somados deem -5):
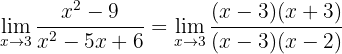
Deste modo, podemos cancelar  para ter
para ter

Assim, o limite é 6.
Calcule o seguinte limite:
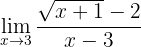
Limites de uma função elevada à outra função
Se calculamos a função com 3, podemos observar que
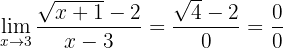
Assim, temos uma indeterminação e devemos fazer uma manipulação algébrica. Neste caso, como temos uma expressão com radicais, devemos multiplicar e dividir a fração pelo conjugado do numerador (já que é ele que tem o radical):
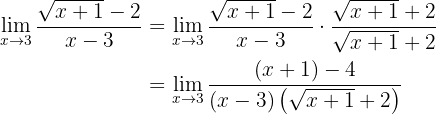
do qual é obtido já que temos “binômios conjugados” no numerador. Simplificando:
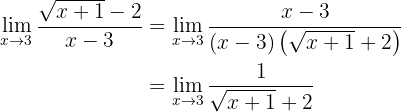
Agora podemos calcular com 3, onde obteremos:
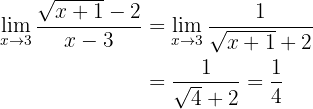
Portanto, o limite é 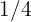 .
.
Calcule o seguinte limite:

Se calculamos no  , obteremos:
, obteremos:

Da qual é uma forma indeterminada. Portanto, devemos fazer manipulações algébricas para obter alguma expressão similar à definição de  . Para isso, primeiro somamos e subtraímos 2 no expoente (indicaremos o limite como
. Para isso, primeiro somamos e subtraímos 2 no expoente (indicaremos o limite como  ):
):
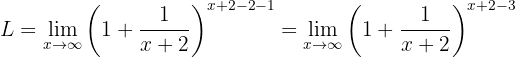
Em seguida usamos as propriedades dos expoentes:

Devemos observar que a primeira potência coincide com a definição de  com
com  . Portanto, o limite é:
. Portanto, o limite é:
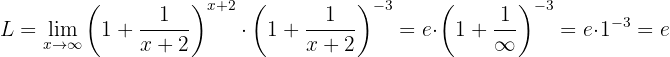
Calcule o seguinte limite:
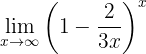
Limites com formas que não são indeterminadas
Ao calcular no infinito, temos:

Portanto, devemos fazer uma manipulação algébrica para obter uma expressão similar à definição de  . Para isso, primeiro modificamos a expressão que temos dentro dos parêntesis (e indicamos o limite como
. Para isso, primeiro modificamos a expressão que temos dentro dos parêntesis (e indicamos o limite como  ):
):

Portanto, no expoente devemos ter  de alguma maneira. Observe que isso é possível quando:
de alguma maneira. Observe que isso é possível quando:

Em seguida usamos as propriedades dos expoentes:
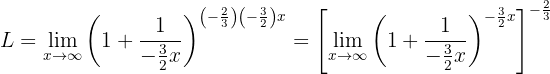
Agora podemos calcular o limite (observando que o que está dentro dos colchetes quadrados é a definição de  com
com 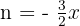 ):
):
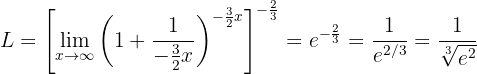
Calcule o seguinte limite:
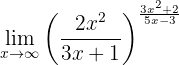
Se calcularmos no  , de imediato vemos que:
, de imediato vemos que:
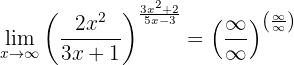
Para resolver isso, usaremos a comparação de infinitos nas duas frações. Primeiro, observe que
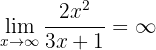
já que o numerador é um polinômio de maior grau (e os coeficientes principais têm o mesmo sinal). De maneira similar,
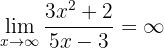
pelo mesmo motivo. Portanto, o limite é:

já que a última expressão não se trata de uma forma indeterminada.
Determine o seguinte limite:
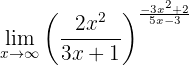
Novamente, se calcularmos no infinito, obteremos:
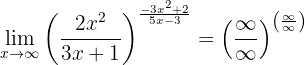
Além disso, se resolvermos os limites das frações (comparando as ordens dos infinitos), podemos observar que:

já que o numerador é um polinômio de maior grau e os coeficientes principais têm o mesmo sinal. Por outro lado,
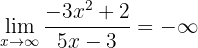
uma vez que o numerador é um polinômio de maior grau, mas os coeficientes principais têm sinal diferente. Deste modo, sabemos que o limite é:

Determine o seguinte limite:
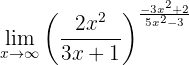
Novamente, se calcularmos no infinito, teremos

Portanto, devemos calcular os limites das frações separadamente. Na base da potência sabemos que o numerador é um polinômio de maior grau, além disso, que os coeficientes principais têm o mesmo sinal, portanto

Por outro lado, no expoente tanto o numerador como o denominador são polinômios com a mesma ordem. Portanto, o limite é o quociente dos coeficientes principais:
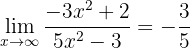
Portanto, o limite é

já que  se
se  .
.
Calcule o seguinte limite:
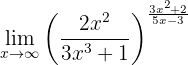
Se calcularmos no infinito, teremos
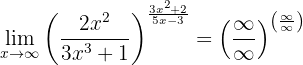
Assim, temos que calcular os limites das frações separadamente para determinar o limite geral. Portanto,
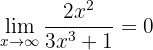
já que o denominador é um polinômio de maior grau. Desse modo,
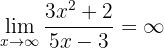
já que o numerador é um polinômio de maior grau e os coeficientes principais têm o mesmo sinal. Portanto, o limite é

já que 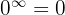 (isto é, não é uma forma indeterminada).
(isto é, não é uma forma indeterminada).
Calcule o seguinte limite:
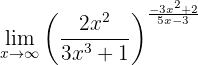
Este limite é praticamente igual ao anterior, porém com um sinal diferente.

Assim, temos que calcular os limites das frações separadamente para determinar o limite geral. Igual que no caso anterior, teremos
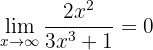
já que o denominador é um polinômio de maior grau. Desse modo, teremos
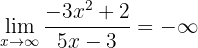
já que o numerador é um polinômio de maior grau e os coeficientes principais têm sinais diferentes. Portanto, o limite é

observe que essa é uma forma indeterminada. Portanto, devemos usar a propriedade:

de modo que
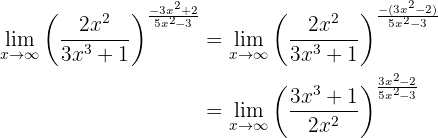
Neste caso,

Assim,
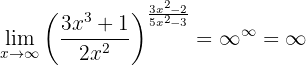
Nota: é importante escrever dessa maneira. O motivo para isso é que  é uma forma indeterminada (ou seja, podemos construir diferentes funções nas quais essa forma indeterminada 'converge' para valores distintos).
é uma forma indeterminada (ou seja, podemos construir diferentes funções nas quais essa forma indeterminada 'converge' para valores distintos).
Calcule o seguinte limite:

Igual que nos casos anteriores, se calcularmos no infinito, obteremos

Igual que nos casos anteriores, calculamos os limites de cada fração separadamente:
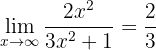
já que o numerador e o denominador são polinômios do mesmo grau (uma vez que o limite é o quociente dos coeficientes principais). Além disso, temos

de modo que o limite é

Calcule o seguinte limite:

Como nos casos anteriores, ao calcular no infinito teremos
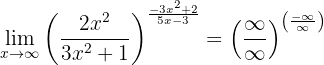
Calculamos os limites de cada fração separadamente:
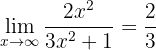
já que o numerador e o denominador são polinômios do mesmo grau (uma vez que o limite é o quociente dos coeficientes principais). Além disso, temos
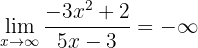
já que o numerador é um polinômio de maior grau e os coeficientes principais têm sinais diferentes. Assim, o limite é

já que temos um, uma expressão da forma 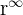 onde
onde  .
.
Determine o seguinte limite:
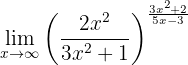
Como nos casos anteriores, ao calcular no infinito, teremos
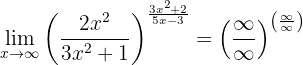
observe que a função é praticamente a mesma que a anterior, mas apenas com um sinal mudado. Calculamos os limites de cada fração separadamente:
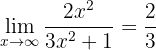
já que o numerador e o denominador são polinômios do mesmo grau (uma vez que o limite é o quociente dos coeficientes principais). Além disso, temos
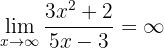
já que o numerador é um polinômio de maior grau e os sinais dos coeficientes principais são iguais. Dessa forma, o limite é
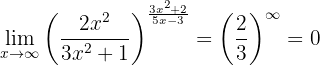
já que temos um, uma expressão da forma 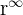 onde
onde  0 < r < 1[/latex].
0 < r < 1[/latex].
Resumir com IA:












