Temas
- Sistema com 3 equações e 2 incógnitas
- Sistema com 2 equações e 3 incógnitas
- Sistema com 3 equações e 3 incógnitas com coeficientes semelhantes
- Sistema com 3 equações e 3 incógnitas
- Verifique se o sistema a seguir é determinado ou indeterminado
- Sistema com 4 equações e 4 incógnitas
- Verifique se o sistema com 4 equações é indeterminado
- Resolva o sistema com 3 equações e 5 incógnitas
- Resolva o sistema com 4 equações e 3 incógnitas
A eliminação por escalonamento, também conhecida como método de Gauss, é uma técnica da álgebra linear usada para resolver sistemas de equações lineares e encontrar a forma escalonada ou forma reduzida por linhas de uma matriz, simplificando os cálculos.
Nesta sequência de exercícios, vamos trabalhar com diferentes tipos de sistemas e aplicar a eliminação de Gauss passo a passo. Isso vai te ajudar a reforçar o entendimento e a desenvolver habilidades essenciais para a resolução de problemas algébricos.
Vamos colocar a mão na massa e praticar!
Sistema com 3 equações e 2 incógnitas
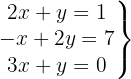
Escrevemos na forma matricial:
Aplicamos o escalonamento da matriz (eliminação de Gauss)
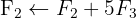
O sistema é possível e determinado
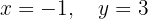
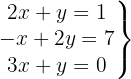
Escrevemos na forma matricial:
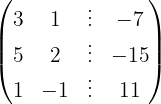
Aplicamos a eliminação por escalonamento (método de Gauss):
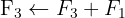
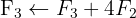
O sistema é possível e determinado:
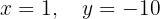
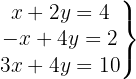
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
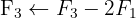
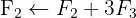
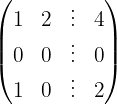
O sistema é possível e determinado:
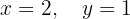
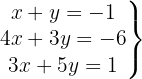
Escrevemos na forma matricial:
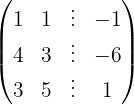
Aplicamos a eliminação por escalonamento (método de Gauss):
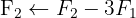
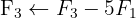
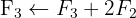
O sistema é possível e determinado:
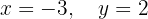
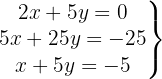
Escrevemos na forma matricial:
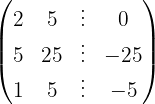
Aplicamos a eliminação por escalonamento (método de Gauss):
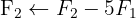
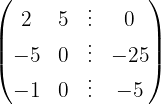
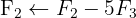
O sistema é possível e determinado:
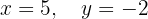
Sistema com 2 equações e 3 incógnitas
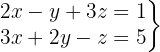
Escrevemos na forma matricial:
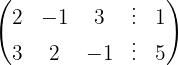
Aplicamos a eliminação por escalonamento (método de Gauss):
O sistema é possível e indeterminado.
Realizamos uma parametrização da solução utilizando 
. Desse modo, a segunda equação fica:
Ou seja,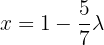 
.
Por outro lado, a primeira equação do sistema fica: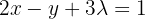 
, ao isolar: 
, vamos obter:
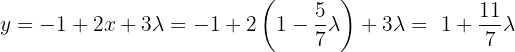
Ou seja,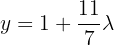 
.
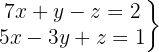
Escrevemos na forma matricial:
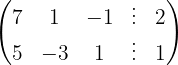
Aplicamos a eliminação por escalonamento (método de Gauss):
O sistema é possível e indeterminado.
Realizamos uma parametrização da solução utilizando 
. Desse modo, a segunda equação fica:
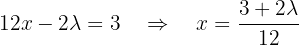
Ou seja, 
.
Por outro lado, a primeira equação fica: 
, que ao isolar 
vamos obter:
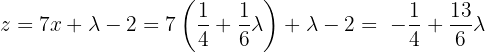
Ou seja,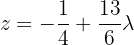 
.
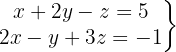
Escrevemos na forma matricial:
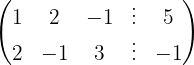
Aplicamos a eliminação por escalonamento (método de Gauss):
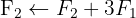
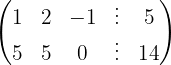
O sistema é possível e indeterminado.
Realizamos uma parametrização da solução utilizando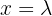 
. Desse modo, a segunda equação fica:
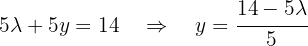
Ou seja,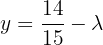 
.
Por outro lado, a primeira equação fica:
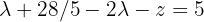, isolando nos dá:
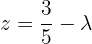
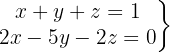
Escrevemos na forma matricial:
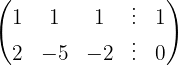
Aplicamos a eliminação por escalonamento (método de Gauss):
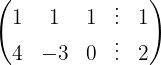
O sistema é possível e indeterminado.
Realizamos uma parametrização da solução utilizando 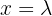. Desse modo, a segunda equação fica:
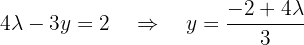
Ou seja,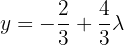 
.
Por outro lado, a primeira equação fica:
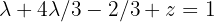, que ao isolar vamos obter:
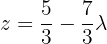
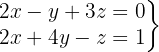
Escrevemos na forma matricial:
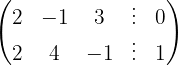
Aplicamos a eliminação por escalonamento (método de Gauss):
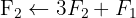
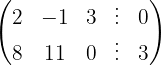
O sistema é possível e indeterminado.
Realizamos uma parametrização da solução utilizando: 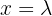. Desse modo, a segunda equação fica:
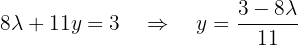
Ou seja, .
Por outro lado, a primeira equação fica: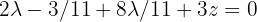 
, isolando, vamos obter:
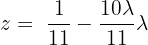
Sistema com 3 equações e 3 incógnitas com coeficientes semelhantes
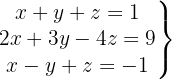
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
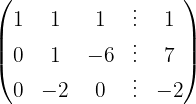
O sistema é possível e determinado.
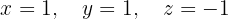
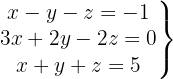
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
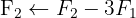
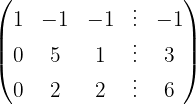
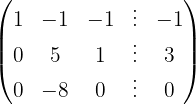
O sistema é possível e determinado.
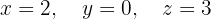
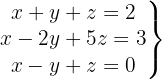
Escrevemos na forma matricial:
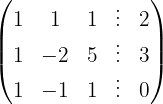
Aplicamos a eliminação por escalonamento (método de Gauss):
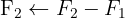
O sistema é possível e determinado.
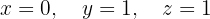
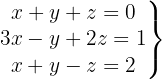
Escrevemos na forma matricial:
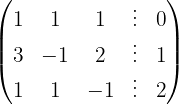
Aplicamos a eliminação por escalonamento (método de Gauss):
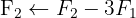
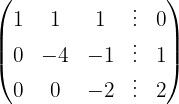
O sistema é possível e determinado.
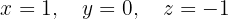
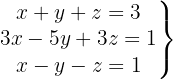
Escrevemos na forma matricial:
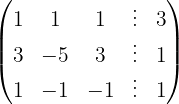
Aplicamos a eliminação por escalonamento (método de Gauss):
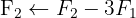
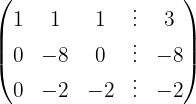
O sistema é possível e determinado.
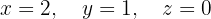
Sistema com 3 equações e 3 incógnitas
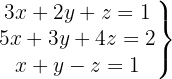
Escrevemos na forma matricial:
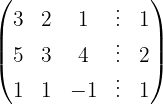
Aplicamos a eliminação por escalonamento (método de Gauss):
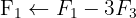
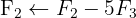
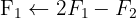
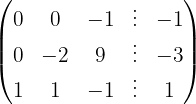
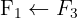
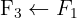
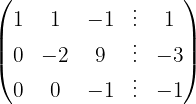
O sistema é possível e determinado.
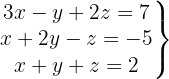
Escrevemos na forma matricial:
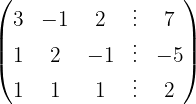
Aplicamos a eliminação por escalonamento (método de Gauss):
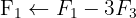
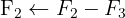
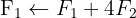
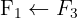
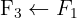
O sistema é possível e determinado.
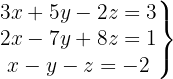
Escrevemos na forma matricial:
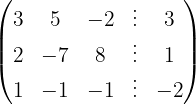
Aplicamos a eliminação por escalonamento (método de Gauss):
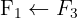
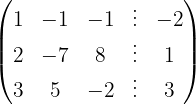
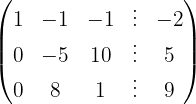
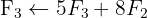
O sistema é possível e determinado.
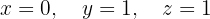
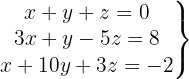
Escrevemos na forma matricial:
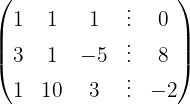
Aplicamos a eliminação por escalonamento (método de Gauss):
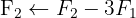
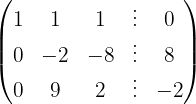
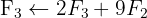
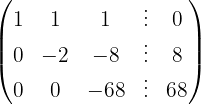
O sistema é possível e determinado.
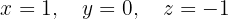
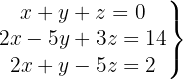
Escrevemos na forma matricial:
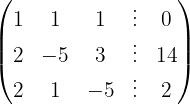
Aplicamos a eliminação por escalonamento (método de Gauss):
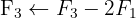
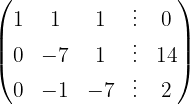
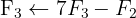
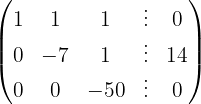
O sistema é possível e determinado.
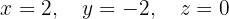
Verifique se o sistema a seguir é determinado ou indeterminado
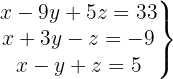
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
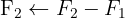
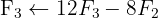
O sistema é possível e indeterminado.
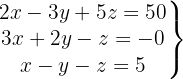
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
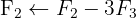
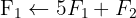
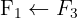
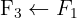
O sistema é possível e determinado.
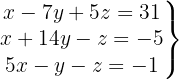
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
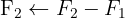
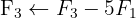
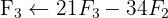
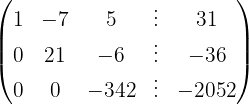
O sistema é possível e determinado.
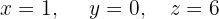
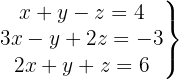
Escrevemos na forma matricial:
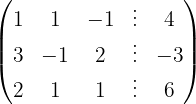
Aplicamos a eliminação por escalonamento (método de Gauss):
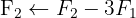
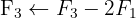
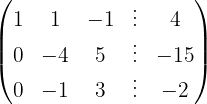
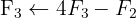
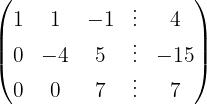
O sistema é possível e determinado.
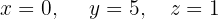
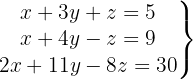
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
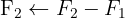
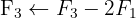
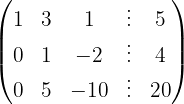
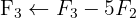
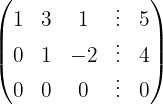
O sistema é possível e indeterminado.
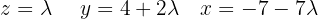
Sistema com 4 equações e 4 incógnitas
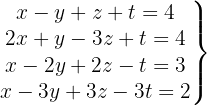
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
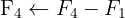
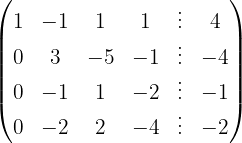
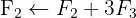
O sistema é possível e indeterminado.
Temos que o sistema é subdeterminado, pois a última linha foi anulada. Vamos parametrizar a solução usando: 
.
A segunda equação torna-se:
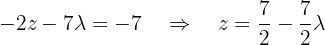
Agora, expressamos em função de 
usando a terceira equação:
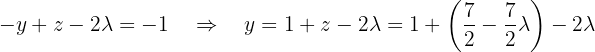
Por fim, utilizamos a primeira equação para encontrar 
em função de: :
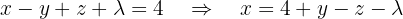
Ou seja,
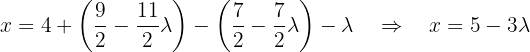
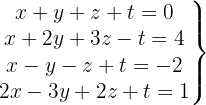
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
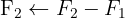
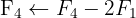
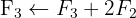
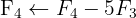
O sistema é possível e determinado.
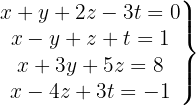
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
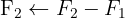
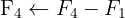
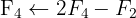
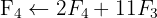
O sistema é possível e determinado.
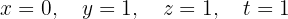
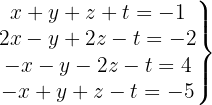
Escrevemos na forma matricial:
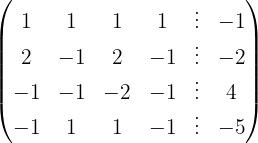
Aplicamos a eliminação por escalonamento (método de Gauss):
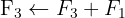
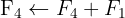
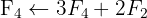
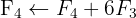
O sistema é possível e determinado.
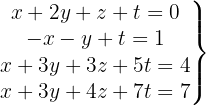
Escrevemos na forma matricial:
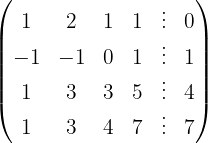
Aplicamos a eliminação por escalonamento (método de Gauss):
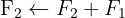
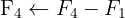
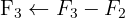
O sistema é possível e indeterminado.
Como a última linha foi anulada, trata-se de um sistema subdeterminado. Vamos parametrizar a solução usando:
.
A terceira equação torna-se:
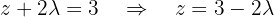
Agora, expressamos em função de usando a segunda equação:
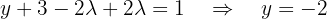
Por fim, usamos a primeira equação para encontrar em função de: :
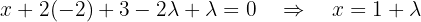
Ou seja,
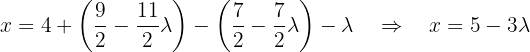
Verifique se o sistema com 4 equações é indeterminado
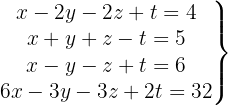
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
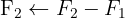
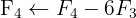
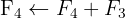
O sistema é possível e indeterminado.
Como a última linha foi anulada, temos um sistema subdeterminado. Vamos parametrizar a solução usando:
.
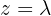A segunda equação torna-se:
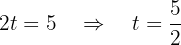
Agora, expressamos em função usando a terceira equação:
Por fim, usamos a primeira equação para encontrar: em função de: :
Assim:
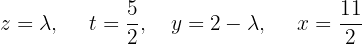
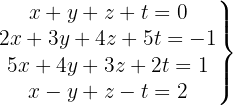
Escrevemos na forma matricial:
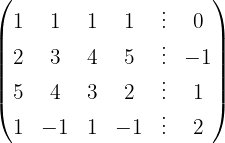
Aplicamos a eliminação por escalonamento (método de Gauss):
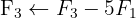
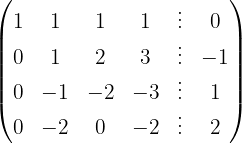
O sistema é possível e indeterminado.
Como a terceira linha foi anulada, trata-se de um sistema subdeterminado. Vamos parametrizar a solução utilizando:
. A segunda equação fica:
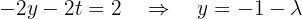
Agora expressamos em função de utilizando a terceira equação:
Por fim, utilizamos a primeira equação para encontrar: em função de :
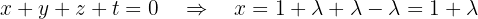
Assim:
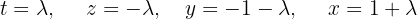
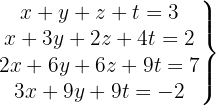
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
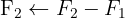
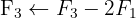
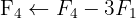
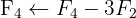
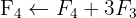
O sistema é incompatível
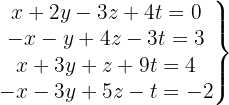
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
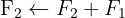
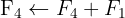
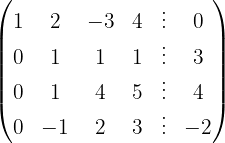
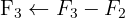
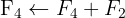
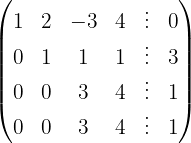
O sistema é possível e indeterminado.
Como a quarta linha foi anulada, trata-se de um sistema subdeterminado. Vamos parametrizar a solução utilizando:
. A terceira equação se torna:
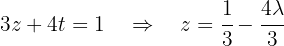
Agora, vamos expressar em função de utilizando a segunda equação:
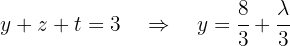
Por fim, a primeira equação é expressa: em função de :
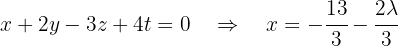
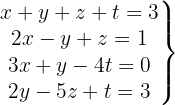
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
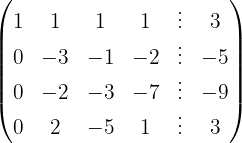
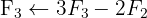
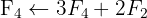
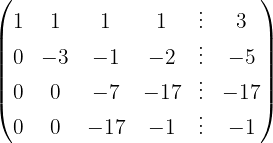
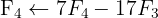
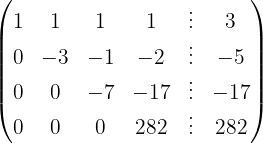
O sistema é possível e determinado.
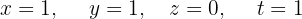
Resolva o sistema com 3 equações e 5 incógnitas
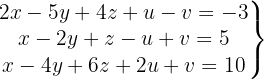
Escrevemos na forma matricial:
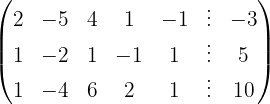
Aplicamos a eliminação por escalonamento (método de Gauss):
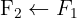
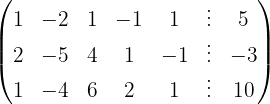
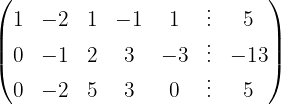
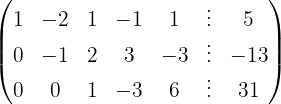
O sistema é possível e indeterminado.
Vamos parametrizar a solução utilizando:
.
A terceira equação se transforma em:
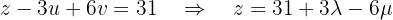
Agora, vamos expressar em função de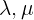 
utilizando a segunda equação, que fica assim:
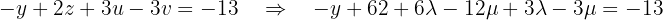
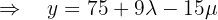
Por fim, utilizamos a primeira equação: para representar em função de :
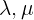Assim,
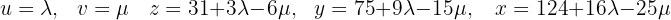
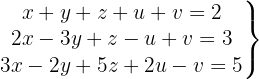
Escrevemos na forma matricial:
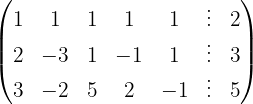
Aplicamos a eliminação por escalonamento (método de Gauss):
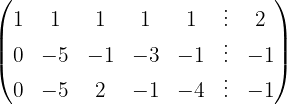
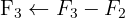
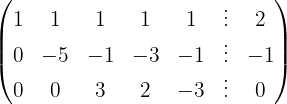
O sistema é possível e indeterminado.
Parametrizamos a solução utilizando .
A terceira equação se torna:
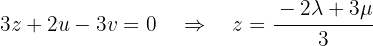
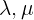Em seguida, expressamos em função de utilizando a segunda equação:
Por fim, utilizamos a primeira equação para expressar em função :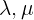
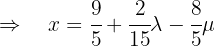
Assim,
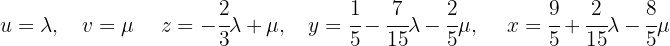
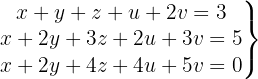
Escrevemos na forma matricial:
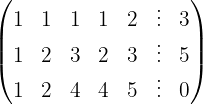
Aplicamos a eliminação por escalonamento (método de Gauss):
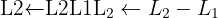
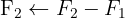
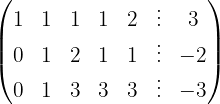
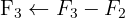
O sistema é possível e indeterminado
Faremos a parametrização da solução utilizando: . De la tercera ecuación se obtiene:
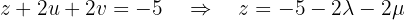
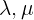Agora expressamos em função de utilizando a segunda equação:
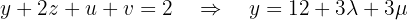
Por fim, utilizamos a primeira equação para expressar em função de :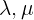
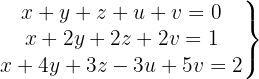
Escrevemos na forma matricial:
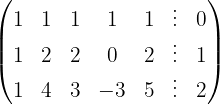
Aplicamos a eliminação por escalonamento (método de Gauss):
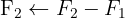
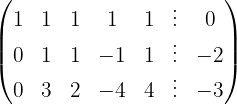
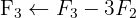
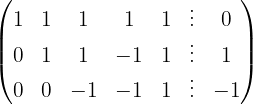
O sistema é possível e indeterminado.
Faremos a parametrização da solução utilizando: .
A terceira equação fornece:
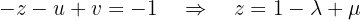
Agora, para encontrar em função de: 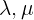substituímos na segunda equação:
Por fim, utilizamos a primeira equação para encontrar em função de :
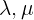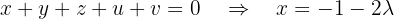
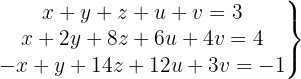
Escrevemos na forma matricial:
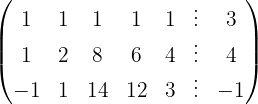
Aplicamos a eliminação por escalonamento (método de Gauss):
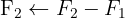
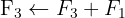
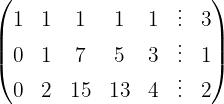
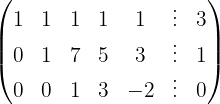
O sistema é possível e indeterminado
Faremos a parametrização da solução utilizando: .
A terceira equação fornece:
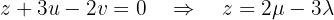
Agora, para encontrar em função de 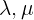utilizado a segund equação:
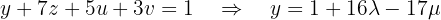
Por fim, utilizamos a primeira equação para encontrar em função de :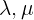
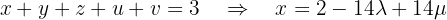
Resolva o sistema com 4 equações e 3 incógnitas
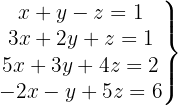
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
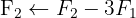
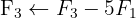
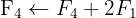
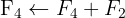
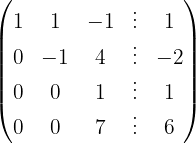
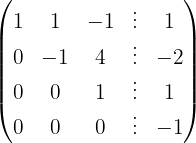
O sistema é incompatível.
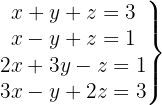
Escrevemos na forma matricial:
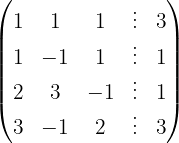
Aplicamos a eliminação por escalonamento (método de Gauss):
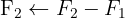
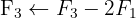
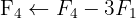
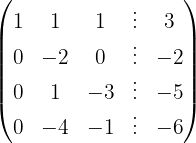
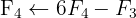
O sistema é possível e determinado
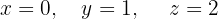
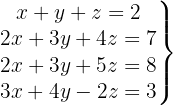
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
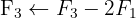
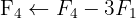
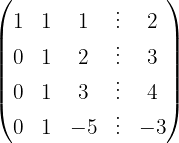
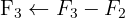
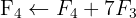
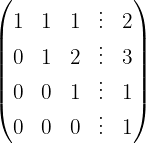
O sistema é incompatível.
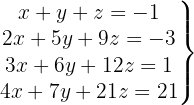
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
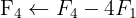
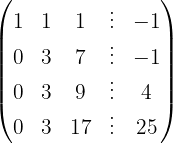
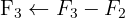
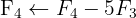
O sistema é incompatível.
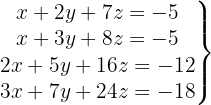
Escrevemos na forma matricial:
Aplicamos a eliminação por escalonamento (método de Gauss):
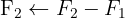
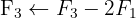
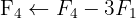
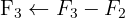
O sistema é incompatível.
Gostou desse artigo? Deixe uma nota!
Loading...
aula boa eu tire 10 na prova
🙌