A função composta é um conceito fundamental no estudo da Matemática, especialmente nos conteúdos de Álgebra e Cálculo. Ela ocorre quando combinamos duas funções de modo que o resultado de uma delas seja usado como entrada da outra. Na matemática, representamos isso por 
, o que indica que aplicamos primeiro a função 
e, em seguida, usamos esse resultado como entrada na função 
.
Entender como as funções estão interligadas é essencial para compreender situações em que uma variável depende de outra, o que é muito comum em problemas matemáticos e em contextos do cotidiano. Ao longo desta série de exercícios resolvidos, vamos explorar diferentes casos em que aparece a função composta, com o objetivo de reforçar o aprendizado e desenvolver a habilidade dos estudantes para lidar com esse tipo de operação com clareza e segurança.
Analise as seguintes funções compostas:
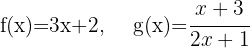
Calcule:
a
b
a
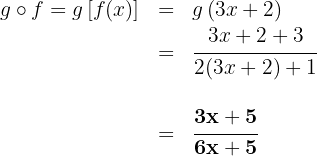
b
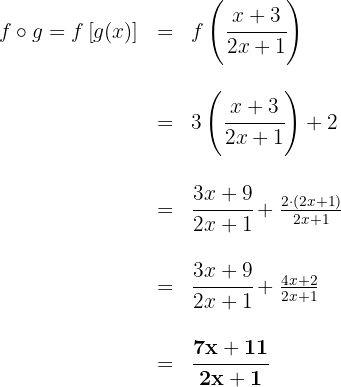
Considere as funções compostas:
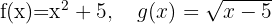
Determine:
a
b
a
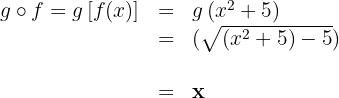
b
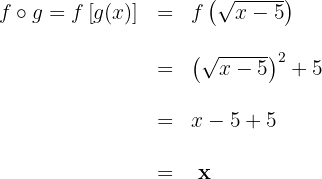
Analise as seguintes funções compostas:
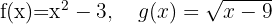
Determine:
a
b
a
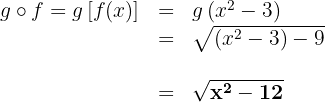
b
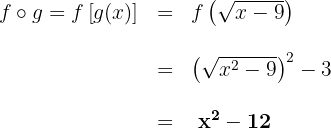
Considere as seguintes expressões:
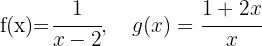
Calcule:
a
b
a
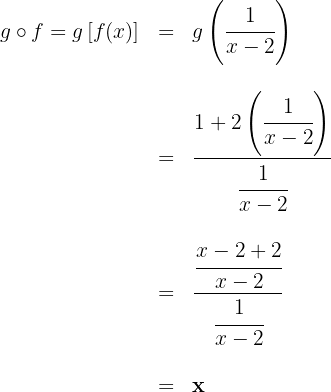
b
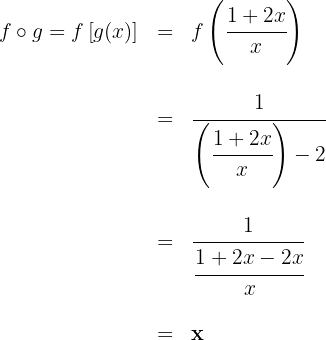
Analise as seguintes funções compostas:
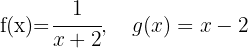
Determine:
a
b
a
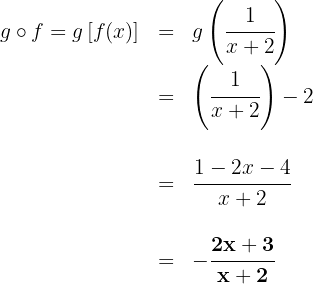
b
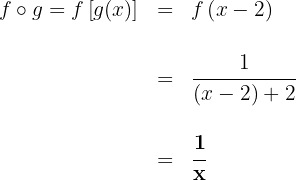
Considere as funções compostas:
Calcule:
a
b
a
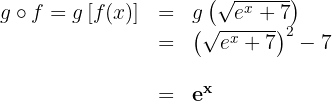
b
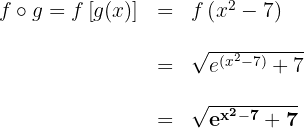
Analise as seguintes funções compostas:
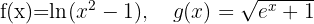
Calcule:
a
b
a
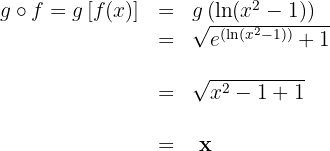
b
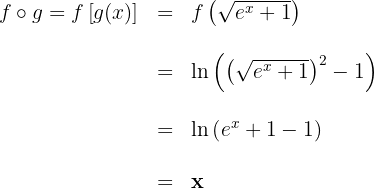
Analise as seguintes funções compostas:
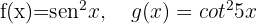
Calcule:
a
b
a
b
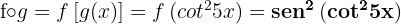
Considere as funções compostas:
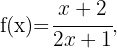
Calcule:
a
b
c
d Comprove que: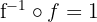 
a
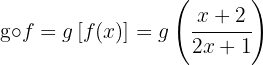
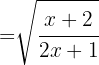
b
c
Para calcular , escrevemos a função 
assim:
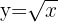
Isolamos 
Trocamos por e 
por
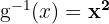
d Comprove que: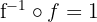
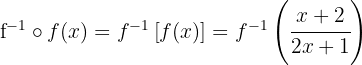
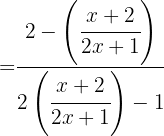
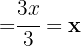
A função composta de uma função com sua inversa é a função identidade.
Considere as seguintes expressões:
, 
, 
Calcule:
a
b
c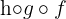
d
e
f Comprove que: 
g Comprove que: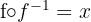 
a
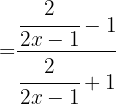
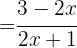
b
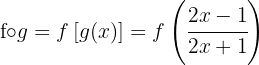
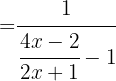
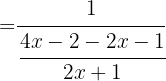
c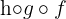
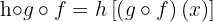
Sabemos que, 
logo,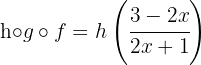 
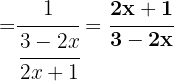
d
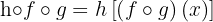
Sabemos que,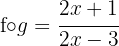 
Dessa forma, 
e
Para calcular , vamos escrever a função dessa forma:
e isolar a variável
Trocamos por e por
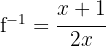
f Comprove que:
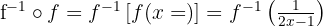
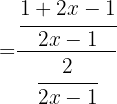
g Comprove que: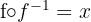
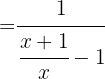
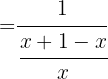
A função composta de uma função com sua inversa é a função identidade.
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
