Permutações com repetições
O número de maneiras distintas em que se podem ordenar os elementos de um conjunto é chamado de uma permutação. Em uma permutação, importa a ordem dos elementos.
Se não se repetem os elementos no conjunto, o total de maneiras em que se podem colocar mmm elementos em grupos de tamanho n é dado pela fórmula
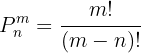
Se, no caso, m=n , para calcular o total de permutações, utiliza-se a seguinte fórmula:
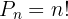
Se os elementos se repetem no conjunto, ou seja, o primeiro elemento repete 
vezes, o segundo 
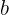vezes e assim, sucessivamente, sendo 
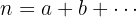, o número de permutações tendo em consideração os elementos repetidos é obtido com a fórmula:
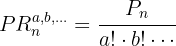
Exercícios de permutações
Quantos números de 5 dígitos diferentes podem ser formados com os dígitos: 1, 2, 3, 4, 5?
Estabelecemos as condições do exercício:
Todos os elementos são utilizados.
A ordem importa.
Os elementos não se repetem, pois o enunciado exige que os dígitos sejam diferentes.
Trata-se de uma Permutação, portanto utilizamos a fórmula: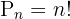
Substituímos e resolvemos: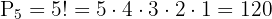
De quantas formas distintas oito pessoas podem se sentar em uma fila de cadeiras?
Estabelecemos as condições do exercício:
Todos os elementos são utilizados, pois as 8 pessoas devem se sentar.
A ordem importa.
Os elementos não se repetem, pois uma pessoa não pode ocupar mais de um lugar.
Trata-se de uma Permutação, portanto utilizamos a fórmula: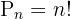
Substituímos e resolvemos: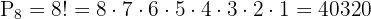
De quantas formas distintas oito pessoas podem se sentar ao redor de uma mesa redonda?
Estabelecemos as condições do exercício:
Todos os elementos são utilizados, pois as 8 pessoas devem se sentar.
Por ser um arranjo circular, eliminamos as repetições circulares.
Os elementos não se repetem, pois uma pessoa não pode ocupar mais de um lugar.
Trata-se de uma Combinação, portanto utilizamos a fórmula: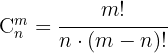
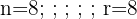
Substituímos e resolvemos: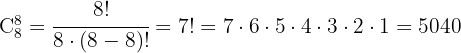
Com os dígitos 2, 2, 2, 3, 3, 3, 3, 4, 4, quantos números de nove dígitos podem ser formados?
Temos 3 elementos distintos que se repetem: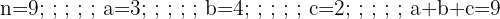
Trata-se de uma permutação com elementos repetidos, portanto utilizamos a fórmula: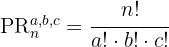
Substituímos na fórmula e resolvemos: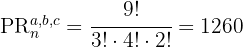
Com as letras da palavra "livro", quantas ordenações distintas podem ser feitas que comecem por vogal?
A palavra deve começar com "i" ou "o", seguida das 4 letras restantes, tomadas de 4 em 4.
Estabelecemos as condições:
Todos os elementos são utilizados.
A ordem importa.
Os elementos não se repetem.
Como temos 2 vogais possíveis para iniciar, calculamos o resultado com: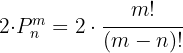
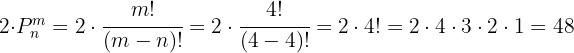
Quantos números de cinco dígitos distintos podem ser formados com os algarismos ímpares? Quantos deles são maiores que 70.000?
Estabelecemos as condições:
Sim, todos os elementos são usados.
Sim, a ordem importa.
Não há repetição de elementos.
Para encontrar os números de cinco dígitos usando os algarismos ímpares (1,3,5,7,9), usamos a seguinte fórmula:
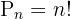
Substituímos e resolvemos:
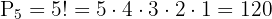
Para encontrar os números que sejam maiores que 70.000, consideramos aqueles que começam com 7 ou 9:
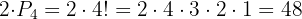
No mastro de sinais de um navio, podem ser hasteadas três bandeiras vermelhas, duas azuis e quatro verdes. Quantos sinais distintos podem ser indicados com a disposição dessas nove bandeiras?
Temos três elementos a, b, c, que se repetem:
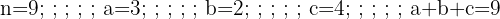
Como se trata de uma permutação com elementos repetidos, utilizamos a fórmula:
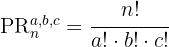
Substituímos na fórmula e resolvemos:
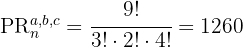
De quantas formas os 11 jogadores de um time de futebol podem ser posicionados, considerando que o goleiro deve ocupar exclusivamente a posição de goleiro?
1 Estabelecemos as condições do exercício:
Temos 10 jogadores que podem ocupar 10 posições distintas.
Sim, todos os elementos são usados.
Sim, a ordem importa.
Não há repetição de elementos.
Trata-se de uma permutação, portanto, utilizamos a fórmula:
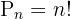
Substituímos e resolvemos:
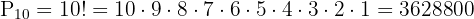
Uma mesa presidencial é formada por oito pessoas. De quantas formas distintas elas podem se sentar, se o presidente e o secretário sempre devem ficar juntos?
Consideramos as duas pessoas que devem permanecer juntas como uma única unidade, o que pode ocorrer de 2! maneiras. Agora restam sete pessoas para se sentarem ao redor da mesa, obedecendo às seguintes condições:
Todos os elementos são utilizados.
A ordem importa.
Os elementos não se repetem.
É possível resolver o exercício com:
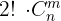
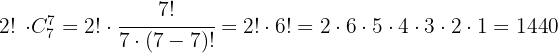
Quatro livros diferentes de matemática, seis diferentes de física e dois diferentes de química são colocados em uma estante. De quantas formas distintas é possível organizá-los se:
- Os livros de cada disciplina devem permanecer juntos.
- Apenas os livros de matemática devem permanecer juntos.
a) Os livros de cada disciplina devem permanecer juntos.
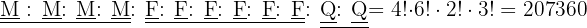
b) Apenas os livros de matemática devem permanecer juntos.
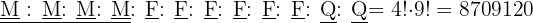
São cinco bolas rosas, duas bolas brancas e três bolas azuis são organizadas em uma fila. Se as bolas da mesma cor não são distinguíveis entre si, de quantas formas diferentes podem ser organizadas?
Temos 3 elementos a, b, c, que se repetem:
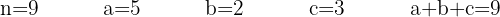
Como se trata de uma permutação com vários elementos repetidos, portanto usamos a fórmula:
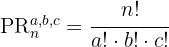
Substituímos na fórmula e resolvemos:
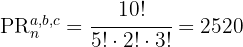
Resolva as equações:
a)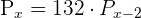 
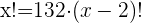
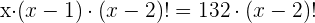
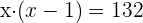
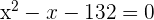
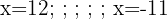
Descartamos o resultado negativo, portanto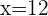 
b) 
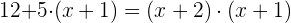
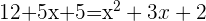
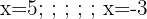
Mais uma vez, descartamos o resultado negativo, portanto 
c)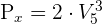 
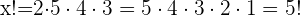
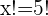
Ficou com alguma dúvida? Na Superprof oferecemos os melhores professores de matemática. Prefere professor de matemática online? Você também poderá encontrá-lo em nossa página.
Gostou desse artigo? Deixe uma nota!
Loading...
