Bem-vindo à nossa página dedicada aos exercícios de máximos e mínimos!
Neste espaço, vamos explorar o fascinante campo da otimização matemática e apresentar os conhecimentos e estratégias necessários para resolver problemas que envolvem a identificação de valores máximos e mínimos de funções.
Os problemas de máximos e mínimos aparecem em diversas áreas do conhecimento, como a física, a economia, a engenharia e muitas outras. Nesses desafios, o objetivo é encontrar os pontos críticos de uma função, ou seja, os pontos em que a derivada é igual a zero, e analisar se eles correspondem a máximos ou mínimos locais.
Aqui, você vai aprender a reconhecer as principais características de uma função que ajudam a identificar seus extremos. Para isso, vamos apresentar uma variedade de exercícios resolvidos usando o critério da segunda derivada, uma ferramenta importante no estudo do comportamento das funções.
Nosso objetivo é ajudar você a desenvolver a habilidade de encontrar soluções ótimas, fortalecer seu raciocínio lógico e analítico, e aumentar a sua confiança na matemática. Aproveite e aprenda com os diferentes exercícios e com as explicações claras e detalhadas que preparamos especialmente para você.
Torne-se um verdadeiro especialista em calcular máximos e mínimos de funções!
Utilize o critério da segunda derivada para calcular os máximos e mínimos locais dos exercícios de funções a seguir:
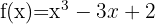
Vamos começar encontrando a primeira e a segunda derivada da função dada:
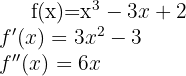
Agora, vamos encontrar os pontos críticos 
resolvendo a equação 
, ou seja,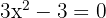 
. As soluções da equação são: 
.
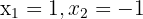Em seguida, vamos avaliar 
nos pontos críticos e determinar se 
ou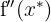 
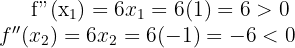
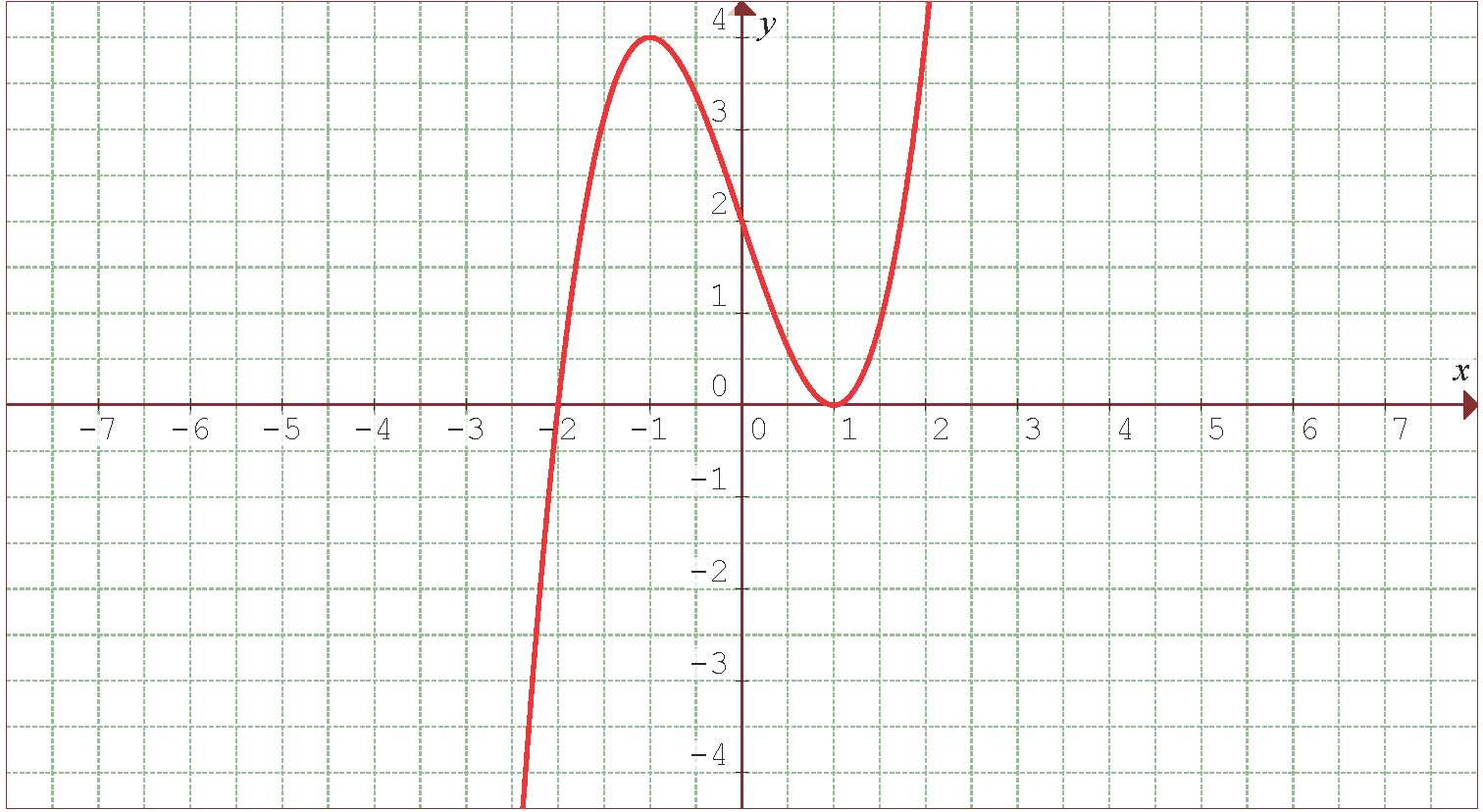
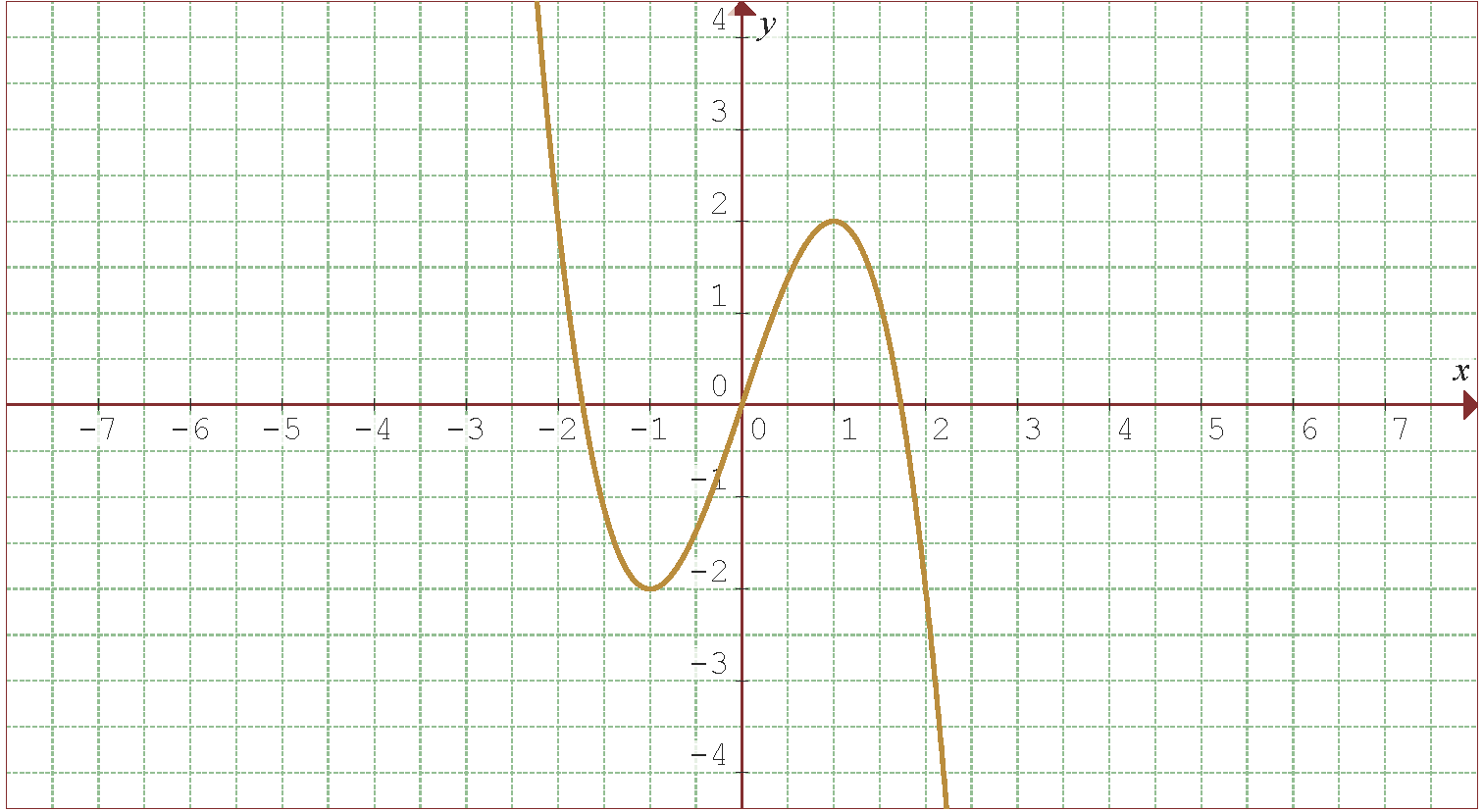
Portanto, pelo critério da segunda derivada, a função 
possui um mínimo local em 
e um máximo local em 
. Os respectivos valores da função são:
A figura a seguir mostra o gráfico da função proposta.
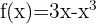
Vamos começar encontrando a primeira e segunda derivada da função:
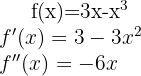
Agora, vamos encontrar os pontos críticos resolvendo a equação , ou seja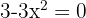 
. As soluções da equação são: 
.
Em seguida, vamos avaliar em seus pontos críticos e determinar se ou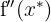
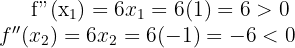
Portanto, pelo critério da segunda derivada, a função tem um máximo local em e um mínimo local em . Os respectivos valores da função são:
A figura a seguir mostra o gráfico da função proposta.
Vamos começar encontrando a primeira e a segunda derivada da função dada:
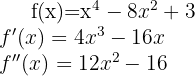
Agora, vamos encontrar os pontos críticos usando o método da equação.
, es decir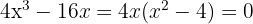 
. Os resultados são:
.
Finalmente, vamos avaliar nos pontos críticos e determinar se ou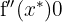 
E, de acordo com o criterio da segunda derivada, a função tem um máximo local em 
e de dois locais mínimos em 
e 
. Os valores que correspondem à função são:
A figura abaixo mostra o gráfico da função .
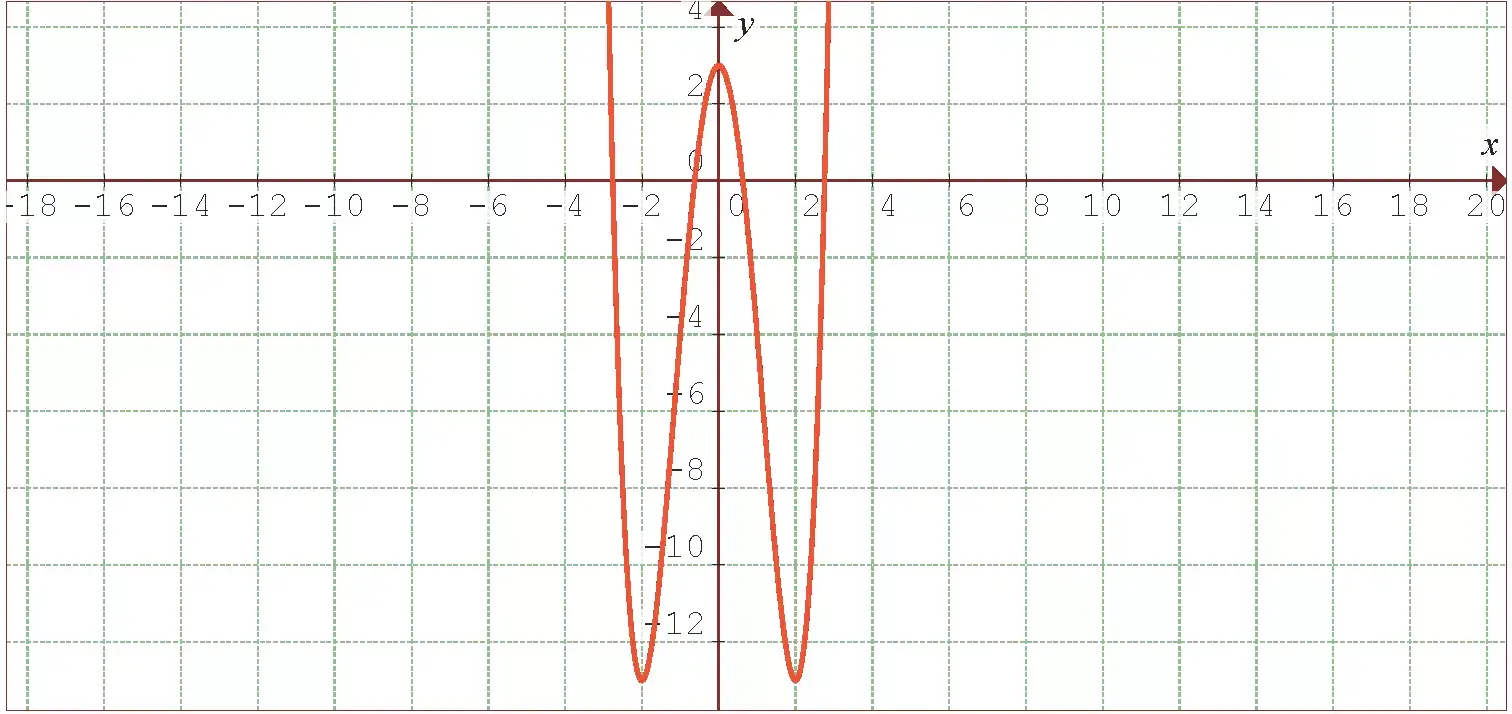
Primeiro, vamos encontrar a primeira e a segunda derivada da função:
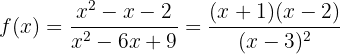
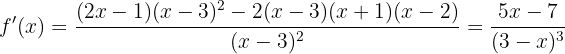
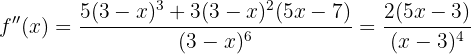
Agora, vamos encontrar o ponto crítico através da solução da equação , ou seja,
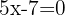, cuja solução é: 
.
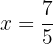Finalmente, vamos avaliar em seu ponto crítico e determinar se ou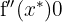 
Assim, pelo criterio da segunda derivada, a função tem um mínimo local em: 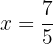. O valor respectivo da função é:
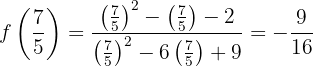
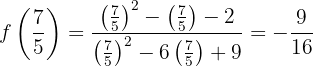
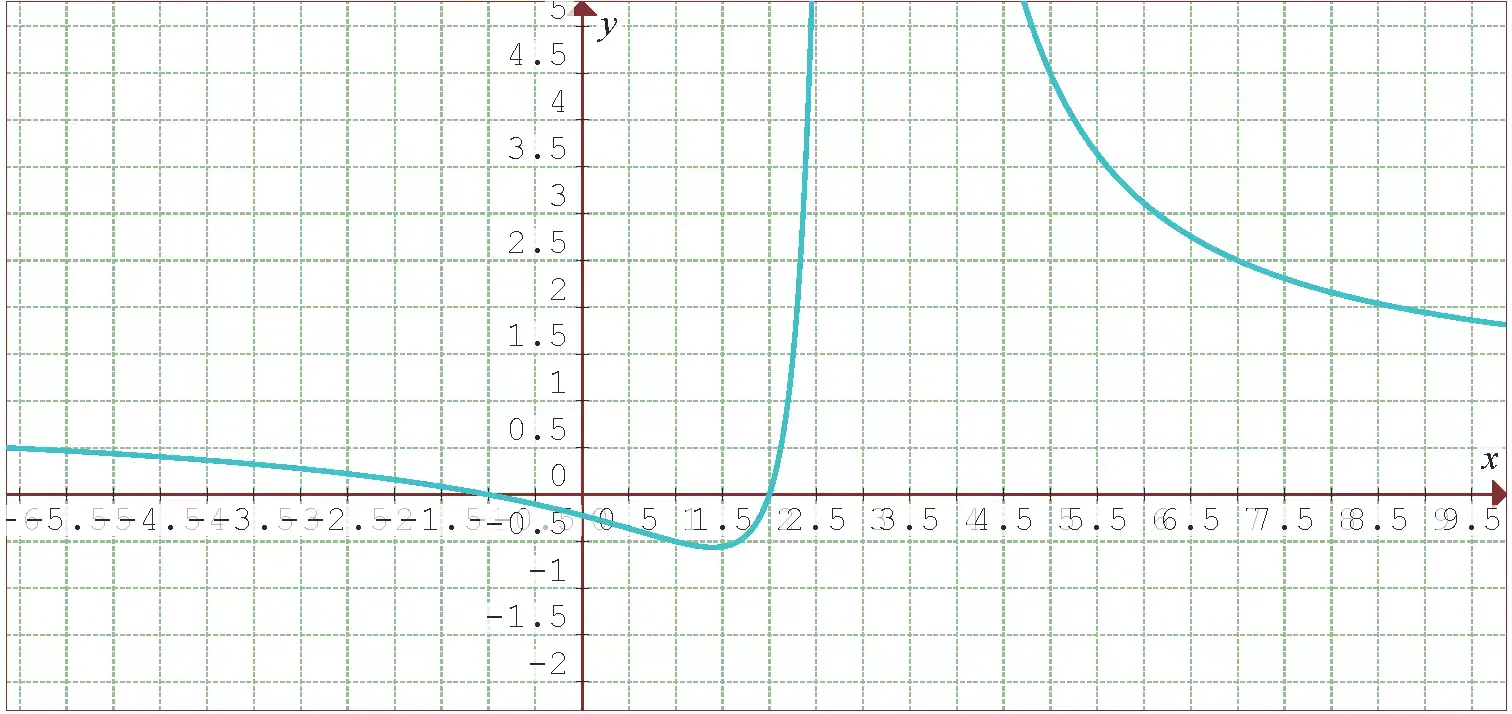
A figura a seguir mostra o gráfico da função proposta.]
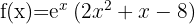
Começaremos encontrando a primeira e a segunda derivada da função:
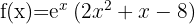
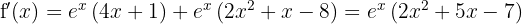
Agora, vamos buscar os pontos críticos através da solução:
da equação, ou seja, 
.
A solução dessa equação são: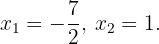 
.
Finalmente, vamos avaliar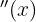 
nos pontos críticos e determinar se 
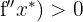ou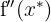
Sendo assim, pelo critério da segunda derivada, a função tem um máximo local em: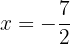 
e um mínimo local em . E os valores correspondentes da função são:
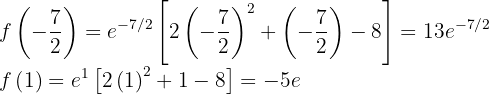
E a representação gráfica é como segue:
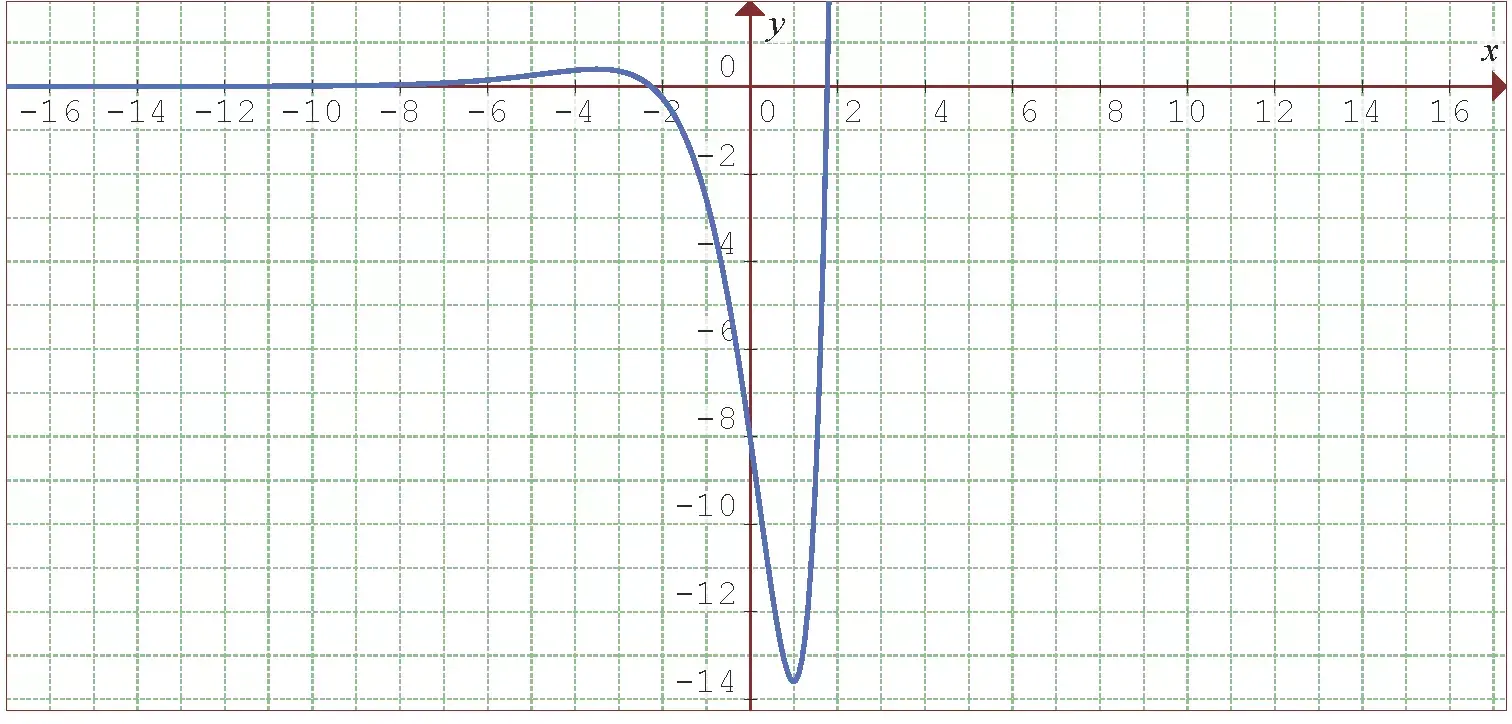
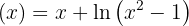
Começaremos encontrando a primeira e a segunda derivada da função:
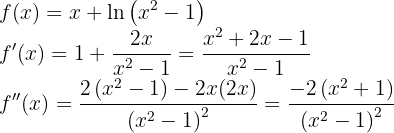
Agora, vamos buscar os pontos críticos através da solução da equação , ou seja,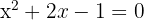 
.
As soluções dessa equação são:
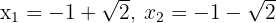. No entanto, considerando que o domínio da função é:
, fica claro que:
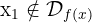
(isso acontece porque: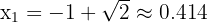 
).
Assim, o único ponto crítico a ser considerado é:
.
Por fim, vamos avaliar no ponto crítico e determinar se 
ou .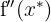
Portanto, ficamos assim:
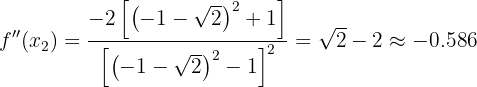tem um máximo local em: 
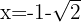. O valor correspondente da função é:
E essa é a representação gráfica da função:
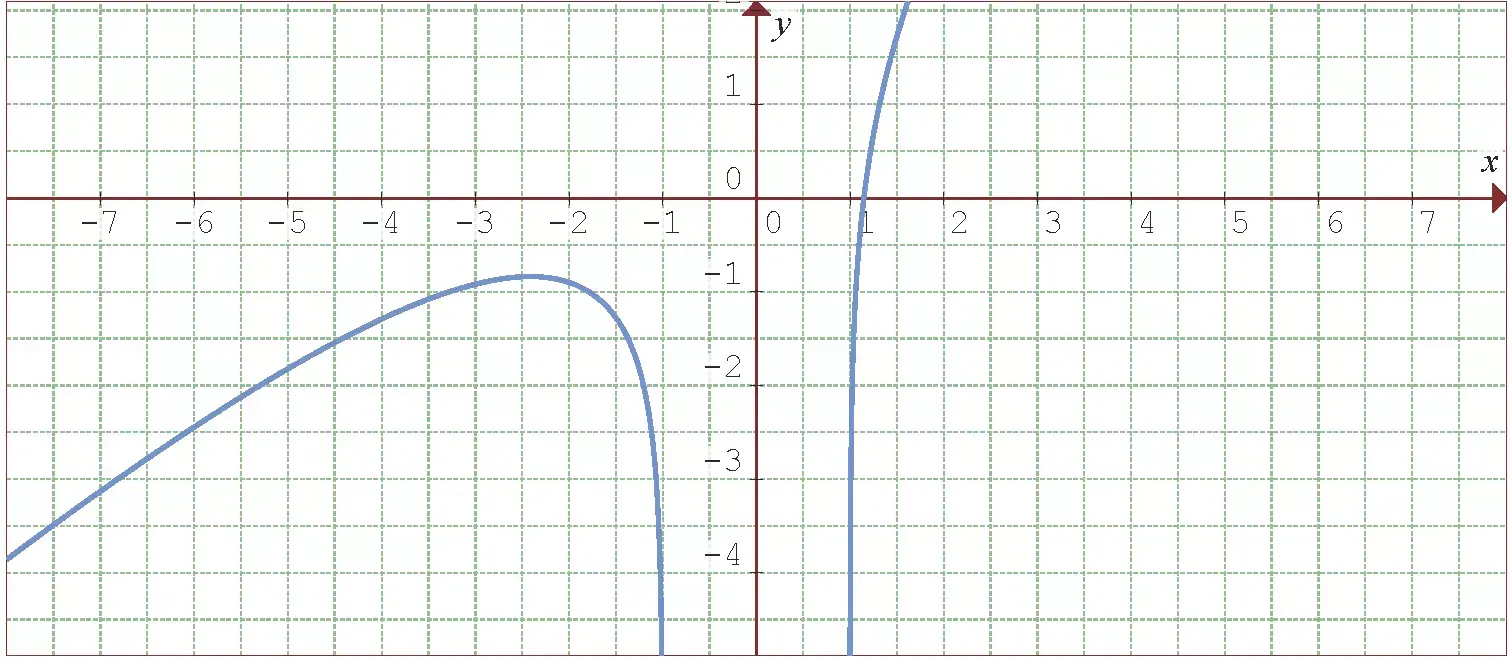
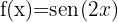
Vamos começar encontrando a primeira e a segunda derivada da função conhecida:
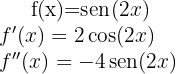
Neste momento, vamos determinas quais são os pontos críticos através da solução da equação , ou seja:
.
Devemos considerar: 
, então: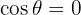 
, dos quais as soluções são dadas por:
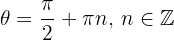
Relembrando a variável da equação original, os pontos críticos conhecidos são:
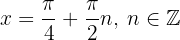
Vamos avaliar nos pontos críticos e determinar se ou 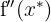(par), então 
, uma vez que:
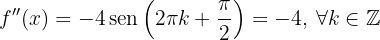
Se 
(impar), então 
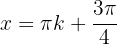, uma vez que:
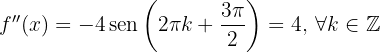
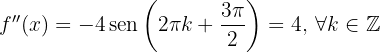
Portanto, pelo critério da segunda derivada, a função tem os máximos locais em: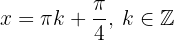 
e os mínimos locais em: 
.
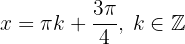E os valores correspondentes para a função são:
A representação abaixo mostra o gráfico da função:
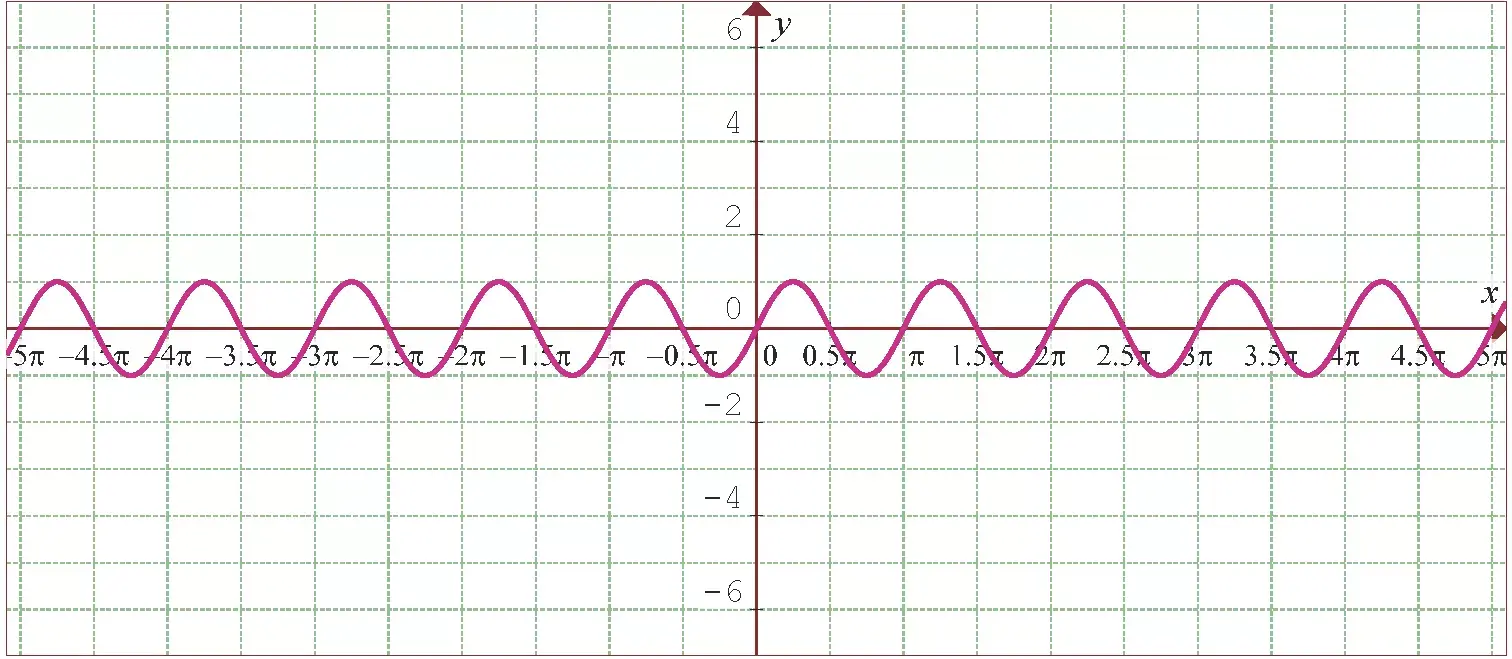
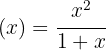
Vamos começar encontrando a primeira e a segunda derivada da função conhecida:
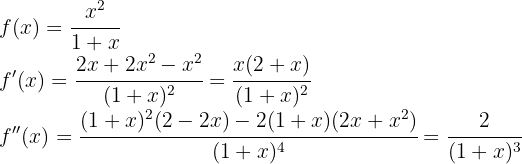
Vamos encontrar os pontos críticos através da solução da equação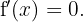 
Vamos ter:
As soluções para essa equação são:
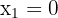e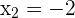 
. Assim, temos apenas dois pontos críticos.
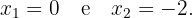
Por fim, vamos fazer a avaliação no ponto crítico e determinar se ou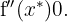 
Então, pelo critério da segunda derivada, a função tem um mínimo local em: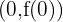 
, ou seja, no ponto:
Agora, vamos avaliar o segundo ponto crítico:
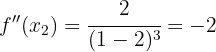tem um máximo local em: 
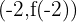, ou seja, 
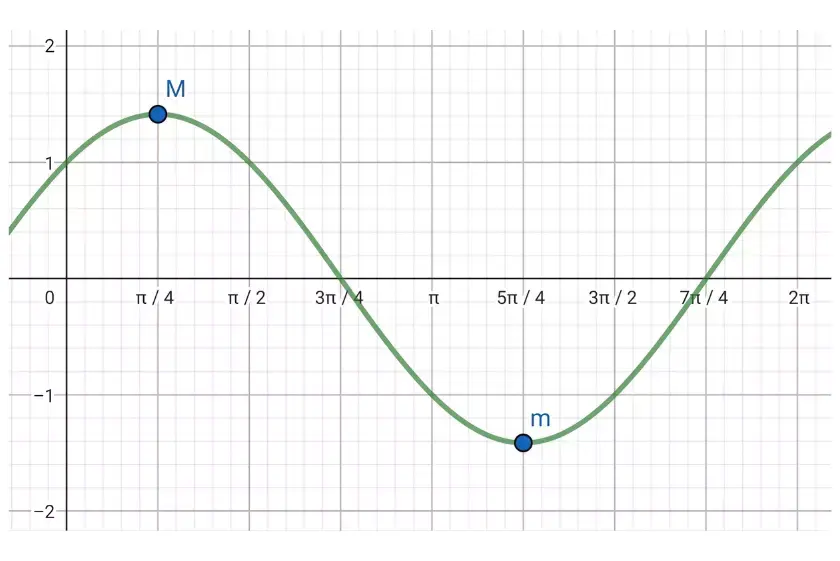
A representação abaixo mostra o gráfico da função
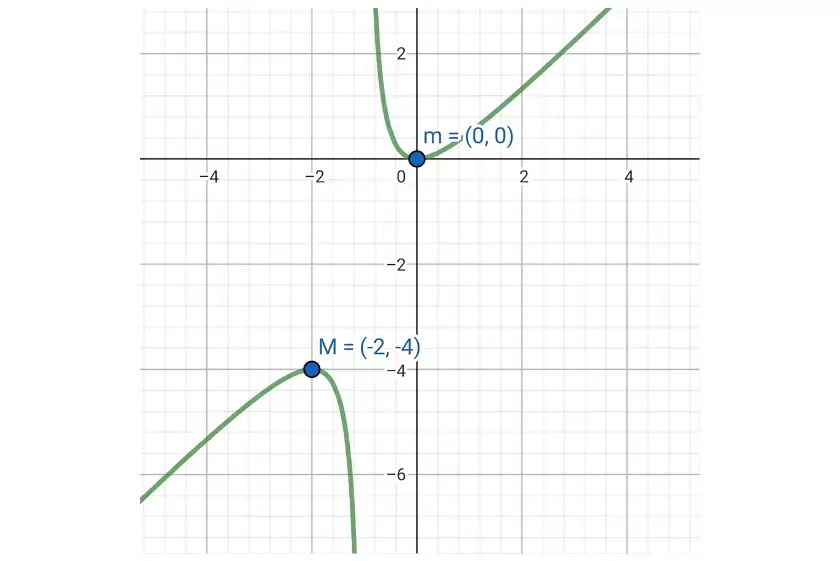
\displaystyle \f(x)=\operatorname{sen}x+\cos x, \quad 0 < x < 2\pi[/latex]
Vamos começar encontrando a primeira e a segunda derivada da função conhecida:
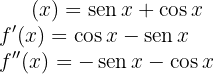
Vamos encontrar os pontos críticos através da soluçãoda equação: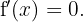
Vamos ter:
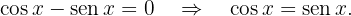
As soluções dessa equação, para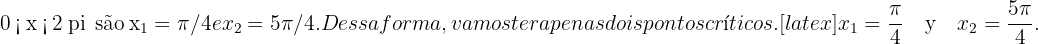 
Agora, vamos avaliar no ponto crítico e determinar se ou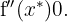
Então, pelo critério da segunda derivada, a função tem um mínimo local em: 
, ou seja, no ponto:
A representação abaixo mostra o gráfico da função dada.
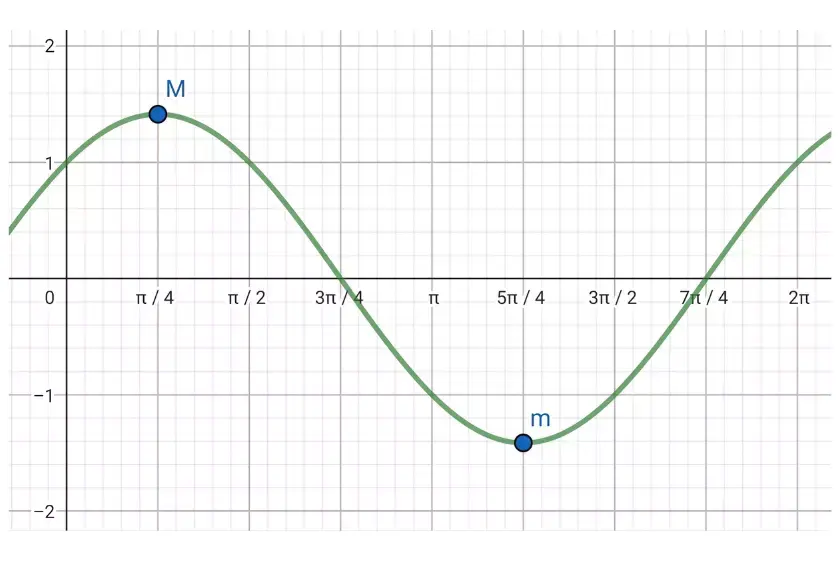
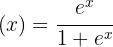
Vamos começar encontrando a primeira e a segunda derivada da função conhecida:
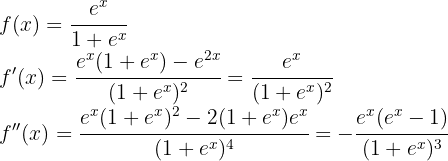
Agora, temos que encontrar os pontos críticos através da solução da equação .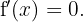
Assim, temos:
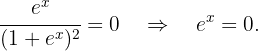
A solução para essa equação é: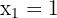 
. Assim, temos um só ponto crítico:.
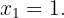
Finalmente, vamos avaliar no ponto crítico e determinar se ou 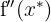tem um máximo local em: 
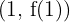, no ponto:
Essa é a figura que representa graficamente conhecida da função:
Gostou desse artigo? Deixe uma nota!
Loading...
