Bem-vindo à nossa página dedicada a exercícios resolvidos de gráficos de funções! Se você está interessado em compreender como as funções matemáticas podem ser visualizadas e analisadas graficamente, chegou ao lugar certo.
Neste espaço, exploraremos conceitos chave relacionados à representação gráfica de funções lineares e e de 2º grau (quadráticas). Fornecermos uma variedade de exercícios práticos e explicações passo a passo para ajudar no desenvolvimento das suas habilidades nesse fascinante campo.
Nestes exercícios, você precisará representar graficamente ou analisar gráficos de funções para extrair informações fundamentais sobre seu comportamento, uma combinação que, sem dúvida, te tornará um verdadeiro especialista nessa área. Mergulhe nesses exercícios fascinantes!

Confira os exercícios sobre retas
Represente as seguintes retas:
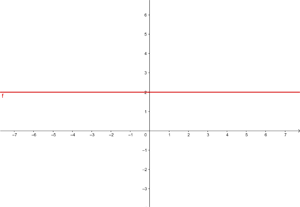
a) 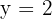
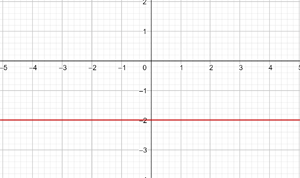
b) 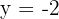
c) 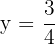
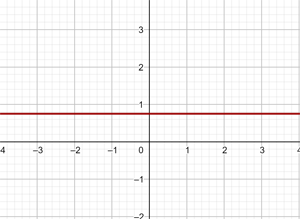
d) 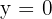
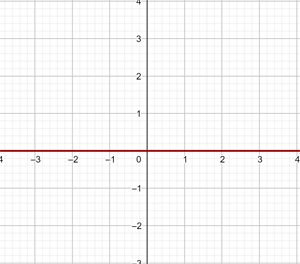
e) 
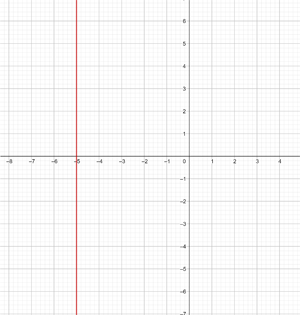
f) 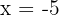
g) 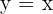
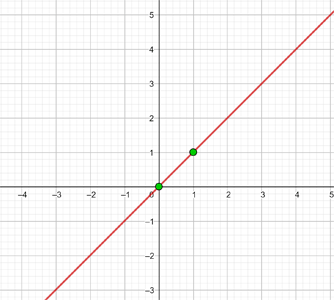
 | 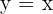 |
|---|---|
 |  |
 |  |
h) 
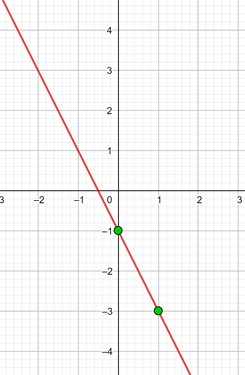
 |  |
|---|---|
 |  |
 |  |
i) 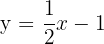
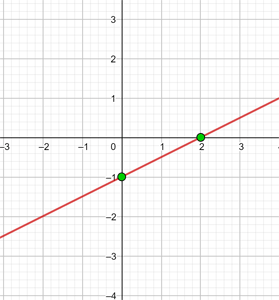
 | 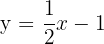 |
|---|---|
 |  |
 |  |
j) 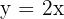
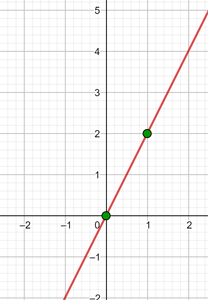
 |  |
|---|---|
 |  |
 |  |
Represente as seguintes funções, sabendo que:
- Tem a inclinação
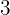

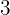 e a ordenada na origem
e a ordenada na origem 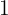

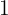 .
. - Tem a inclinação


 e passa pelo ponto
e passa pelo ponto 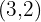
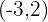
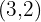 .
. - Passa pelos pontos
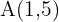
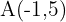
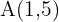 e
e 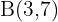
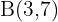
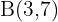 .
. - Passa pelo ponto
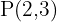
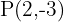
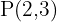 e é paralela à reta de equação
e é paralela à reta de equação 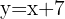
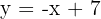
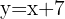 .
.
a) Tem a inclinação 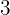

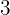 e a ordenada na origem
e a ordenada na origem 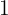

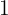 .
.
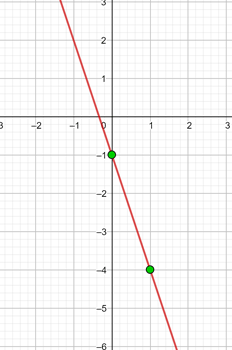
 | 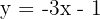 |
|---|---|
 |  |
 |  |
b) Tem a inclinação  e passa pelo ponto (−3, 2).
e passa pelo ponto (−3, 2).
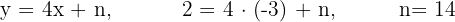
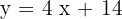
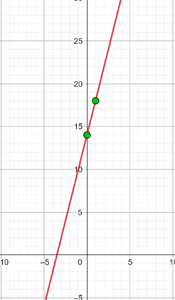
 |  |
|---|---|
 |  |
 |  |
c) Passa pelos pontos 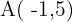 y
y  .
.
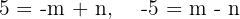

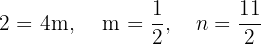

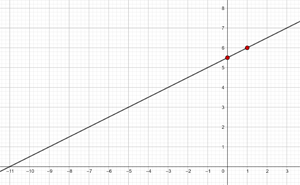
 | 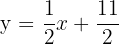 |
|---|---|
 | 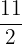 |
 |  |
d) Passa pelo ponto 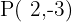 e é paralela a reta da equação
e é paralela a reta da equação 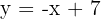 .
.

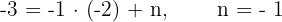

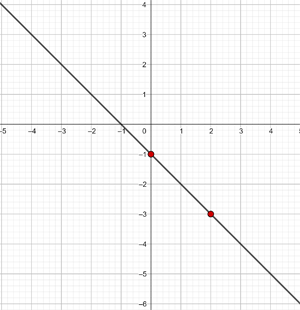
 | 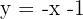 |
|---|---|
 |  |
 |  |
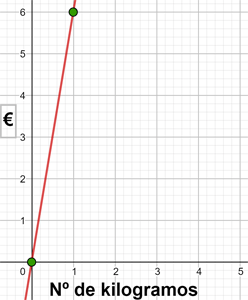
Três kg de camarões valem  €. Escreva e represente a função que define o custo dos camarões em função dos quilogramas comprados.
€. Escreva e represente a função que define o custo dos camarões em função dos quilogramas comprados.
A ordenada na origem é  , que corresponde ao valor de
, que corresponde ao valor de  quilogramas (kg).
quilogramas (kg).
A inclinação é 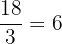
A equação da reta é 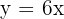
Nas  primeiras semanas de cultivo de uma planta que media
primeiras semanas de cultivo de uma planta que media  cm, observou-se que seu crescimento é diretamente proporcional ao tempo. Na primeira semana, ela passou a medir
cm, observou-se que seu crescimento é diretamente proporcional ao tempo. Na primeira semana, ela passou a medir  cm. Determine uma função afim que forneça a altura da planta em função do tempo e represente graficamente.
cm. Determine uma função afim que forneça a altura da planta em função do tempo e represente graficamente.
Altura inicial  cm é a ordenada na origem.
cm é a ordenada na origem.
Crescimento semanal 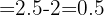 é a inclinação.
é a inclinação.
A equação da reta é 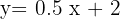 .
.
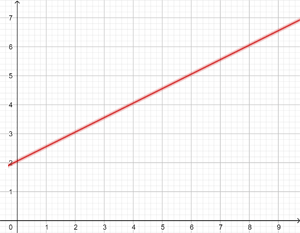
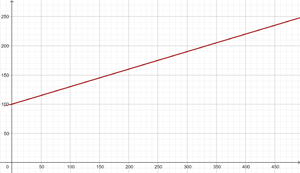
O aluguel de um carro custa R$  por dia, mais R$
por dia, mais R$  por quilômetro rodado. Encontre a equação da reta que relaciona o custo diário com o número de quilômetros percorridos e represente-a. Se em um dia foram percorridos
por quilômetro rodado. Encontre a equação da reta que relaciona o custo diário com o número de quilômetros percorridos e represente-a. Se em um dia foram percorridos  km, qual será o valor a pagar?
km, qual será o valor a pagar?
A ordenada na origem é  e a inclinação é
e a inclinação é  .
.
A equação da reta é 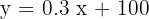 .
.
O valor a ser pago por percorrer  km em um dia é:
km em um dia é: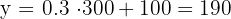 R$
R$
Um salão de eventos oferece um único pacote para  pessoas pelo valor de R$
pessoas pelo valor de R$  . Além disso, a política do salão estabelece que, caso o número de
. Além disso, a política do salão estabelece que, caso o número de  pessoas seja ultrapassado, será cobrado um valor extra de R$
pessoas seja ultrapassado, será cobrado um valor extra de R$  por pessoa a mais.
por pessoa a mais.
Pede-se: represente a função que define esses custos e utilize-a para calcular o valor a ser pago por um excedente de  pessoas.
pessoas.
Como o pacote tem um custo fixo de R$  para até
para até  pessoas, temos uma função constante:
pessoas, temos uma função constante:

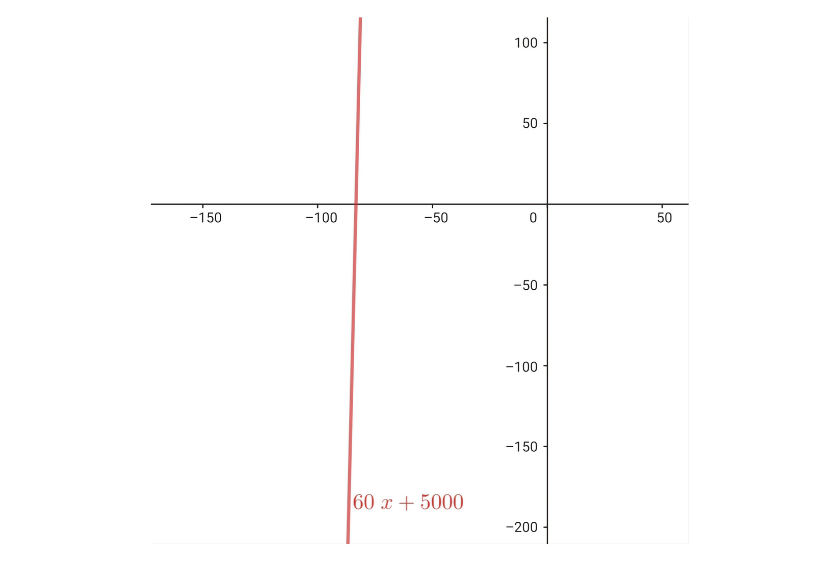
Para cada pessoa extra, o salão cobra R$  . Assim, após
. Assim, após  pessoas, a função deixa de ser constante e passa a ser uma função linear com inclinação
pessoas, a função deixa de ser constante e passa a ser uma função linear com inclinação  , correspondente ao custo adicional por pessoa. Logo, a função, onde a variável independente representa as pessoas adicionais, é:
, correspondente ao custo adicional por pessoa. Logo, a função, onde a variável independente representa as pessoas adicionais, é:
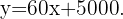
Verificamos que  R$ , correspondendo a
R$ , correspondendo a  pessoas, e
pessoas, e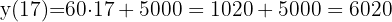 R$, que corresponde ao custo total para um excedente de
R$, que corresponde ao custo total para um excedente de  pessoas.
pessoas.
Uma casa de praia com capacidade para  pessoas tem um custo por noite de R$
pessoas tem um custo por noite de R$ 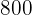 . Além disso, exige-se uma reserva mínima de
. Além disso, exige-se uma reserva mínima de  noites, com a possibilidade de alugar a propriedade por mais
noites, com a possibilidade de alugar a propriedade por mais  noites pelo valor de R$
noites pelo valor de R$  cada uma.
cada uma.
Pede-se: escreva a função que represente essa situação.
O número mínimo de noites exigido para reserva é  . Se cada noite custa R$
. Se cada noite custa R$ 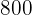 , o valor total para a reserva de
, o valor total para a reserva de  noites é R$
noites é R$  . Isso pode ser representado através da função constante:
. Isso pode ser representado através da função constante:
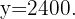
Cada noite extra custa R$  . Para incluir esse fator, passamos para uma função linear. A função é:
. Para incluir esse fator, passamos para uma função linear. A função é:
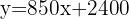
representa o problema, onde a variável independente  representa o número de noites extras.
representa o número de noites extras.
Se o grupo de amigos decide prolongar a estadia por  noites, temos:
noites, temos: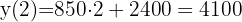 R$
R$
como custo total pelas  noites.
noites.
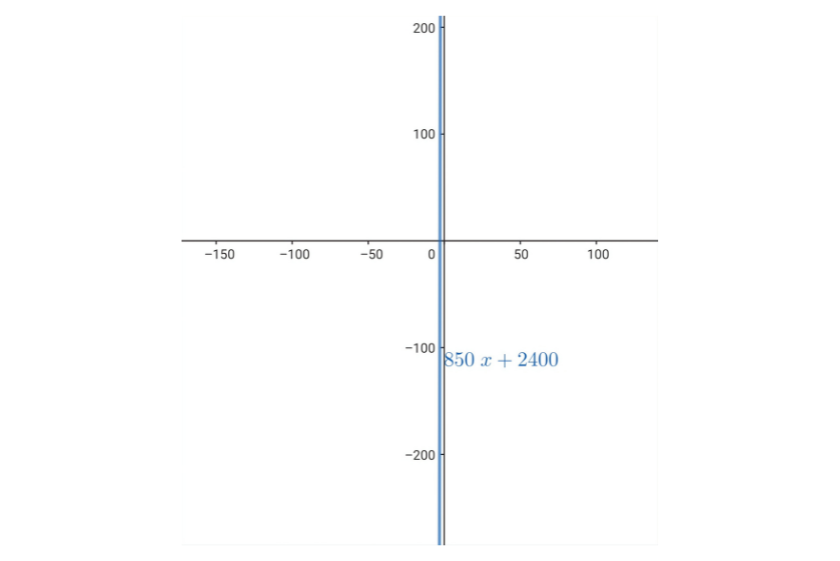
Encontre o vértice e a equação do eixo de simetria das seguintes parábolas:
a) 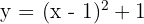
Vértice 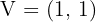
Eixo de simetria 
b) 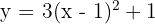
Vértice 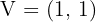
Eixo de simetria 
c) 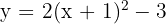
Vértice 
Eixo de simetria 
d) 
Vértice 
Eixo de simetria 
e) 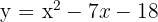
Vértice 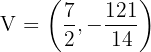
Eixo de simetria 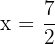
f) 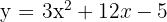
Vértice 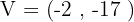
Eixo de simetria 
Represente graficamente as funções 2º grau (quadráticas):
a) 
Calculamos as coordenadas do vértice
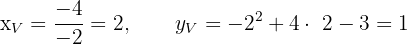
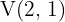
Buscamos os pontos de interseção com o eixo 
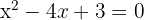


Buscamos o ponto de interseção com o eixo 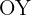
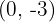
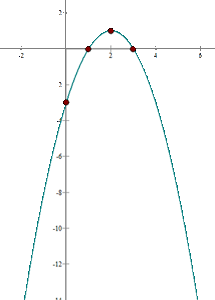
b) 
Calculamos as coordenadas do vértice


Buscamos os pontos de interseção com o eixo 

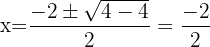
Coincide com o vértice: 
Buscamos o ponto de interseção do eixo 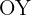
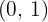
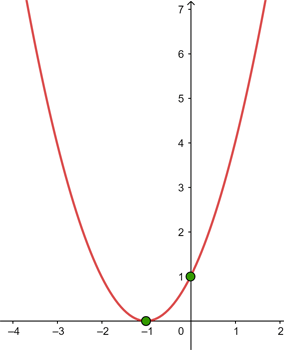
Uma função do segundo grau tem a seguinte forma: 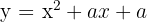 e passa pelo ponto
e passa pelo ponto  . Calcule o valor de
. Calcule o valor de  .
.
Substituímos o ponto na função:
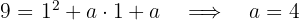
Sabe-se que a função do segundo grau dada por 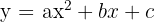 passa pelos pontos
passa pelos pontos 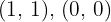 e
e  . Calcule
. Calcule  e
e  .
.
Substituímos o valor de cada ponto em 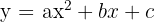 :
:
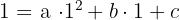
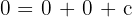
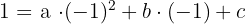
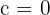
Resolvemos o sistema por redução:

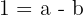


A função do segundo grau é: 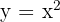 .
.
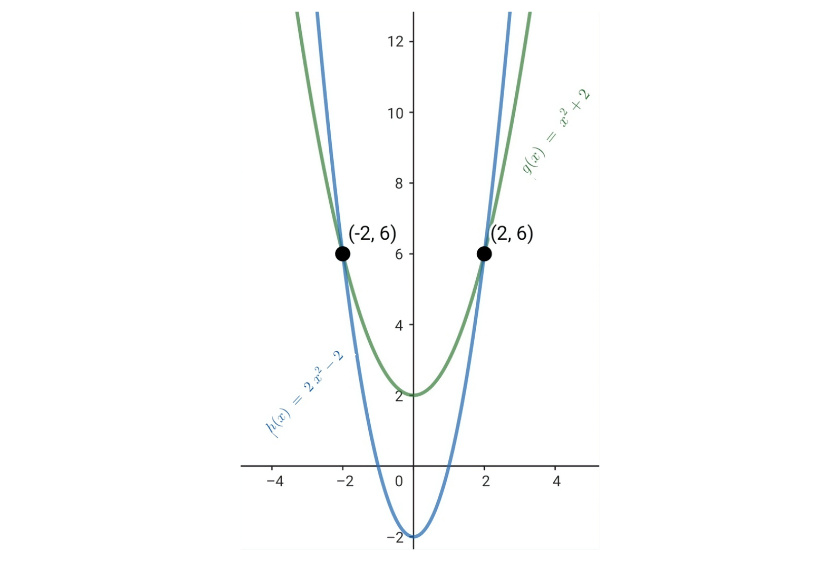
Considere as funções do segundo grau 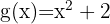 e
e  . Calcule seus pontos de interseção.
. Calcule seus pontos de interseção.
Para encontrar os pontos de interseção dessas funções, igualamos ambas as expressões:

Agora, substituímos esses valores de  em qualquer uma das funções:
em qualquer uma das funções:
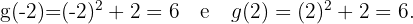
Portanto, os pontos de interseção das funções são:
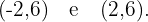
Resumir com IA:












