Temas

Função contínua
Estude a função contínua a seguir:
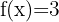
A função é polinomial de grau zero.
O domínio da função polinomial é:  .
.
Portanto, trata-se de uma função contínua em todos os pontos.
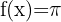
A função é polinomial de grau zero.
O domínio da função polinomial é:  .
.
Portanto, trata-se de uma função contínua em todos os pontos.
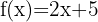
A função é polinomial de grau um.
O domínio da função polinomial é:  .
.
Portanto, trata-se de uma função contínua em todos os pontos.
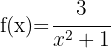
A função é contínua em todos os pontos de seu domínio, exceto nos valores que anulam o denominador.
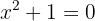
Mas o denominador é sempre positivo, logo, seu domínio é: 
A função é contínua em todos os seus pontos.
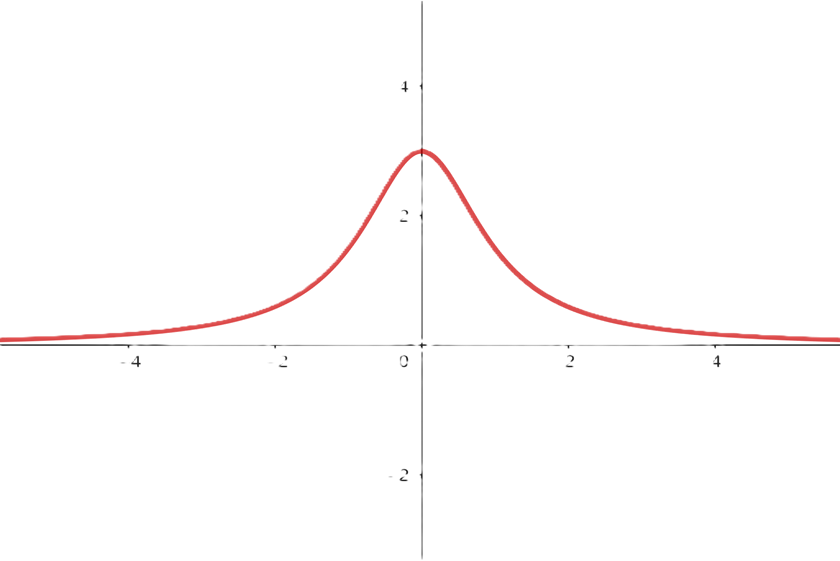
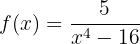
A função é contínua em todos os pontos de seu domínio, exceto nos valores que anulam o denominador.
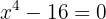

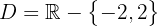
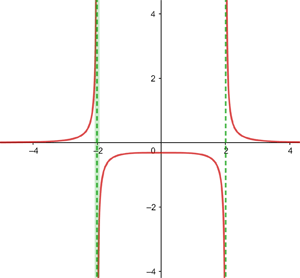
A função é descontinuada em dois pontos:  e
e  .
. 
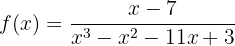
A função é contínua por toda ℛ menos nos valores que anulam o denominador. Se o igualamos a zero e resolver a equação, encontramos a função descontínua nos pontos:

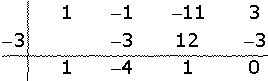
 ; e resolvendo a equação de 2º grau, encontramos:
; e resolvendo a equação de 2º grau, encontramos:
 y
y 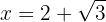
A função é descontínua em 3 pontos:  ,
,  e
e 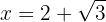
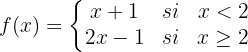
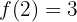
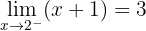
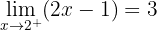
Trata-se de uma função contínua em toda ℛ
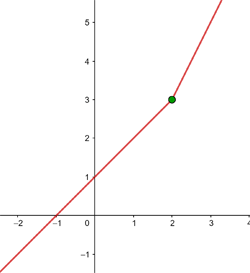
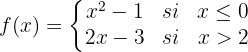

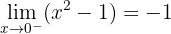

Salto = 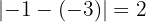
A função é descontinua por salto 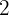 em
em  .
.
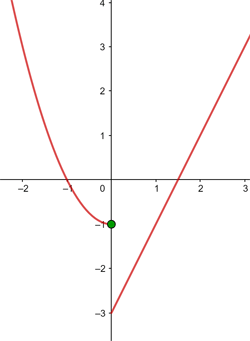
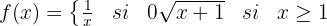
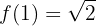
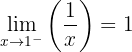
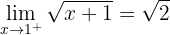
Em  existe uma descontinuidade por salto finito.
existe uma descontinuidade por salto finito.
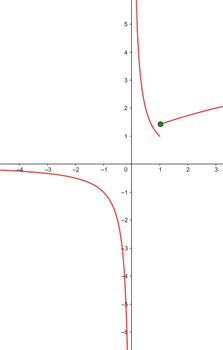
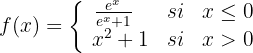
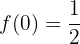


Salto = 
A função é descontínua por salto  em
em  .
.
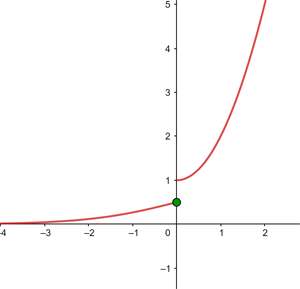
Função contínua no ponto x=0
Estude a função contínua no ponto x=0 a seguir:
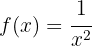
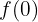 não está definido
não está definido
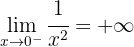
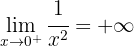
Em  existe uma descontinuidade essencial.
existe uma descontinuidade essencial.
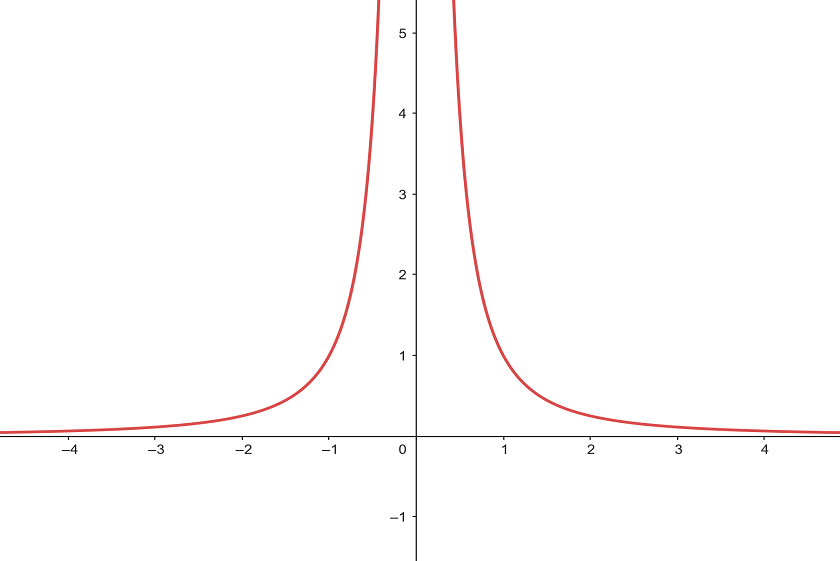
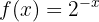

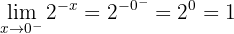

Trata-se de uma função contínua: 
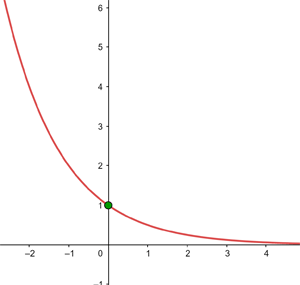
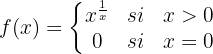
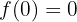
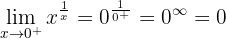
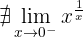
Em  existe uma descontinuidade essencial.
existe uma descontinuidade essencial.
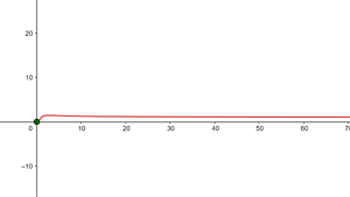
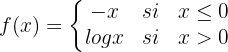
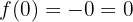
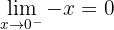
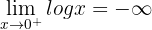
Em  existe uma descontinuidade por salto infinito.
existe uma descontinuidade por salto infinito.
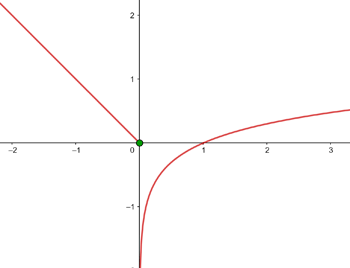
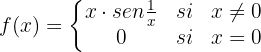
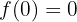
A função 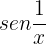 está limitada
está limitada  .
.
Portanto, verifica-se que: 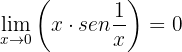
O limite é 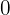 , pois qualquer número multiplicado por zero resulta em zero.
, pois qualquer número multiplicado por zero resulta em zero.
A função é contínua em todo ℛ.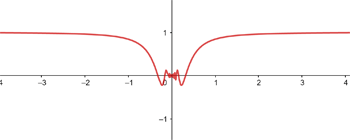
Faça a demonstração da função contínua
Considerando a função:
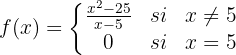
Demonstre que f(x) não é uma função contínua em x = 5.
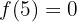
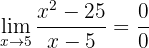
Resolvemos a indeterminação fatorando o numerador e simplificando:
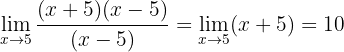
 não é contínua em
não é contínua em  porque:
porque:

Considerando a função:
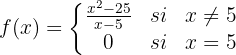
Existe uma função contínua que coincida com  para todos os valores
para todos os valores  ?
?
Se 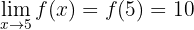 a função seria contínua, então a função redefinida seria:
a função seria contínua, então a função redefinida seria:
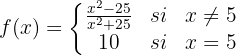
Estudo da continuidade da função:
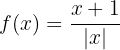
A função  é contínua para
é contínua para 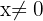 . Vamos estudar sua continuidade em:
. Vamos estudar sua continuidade em:  .
.

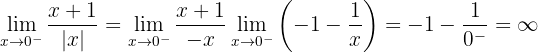
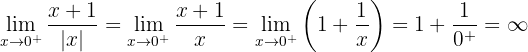
A função não é contínua em  , porque não está definida em
, porque não está definida em  , já que anula o denominador.
, já que anula o denominador.
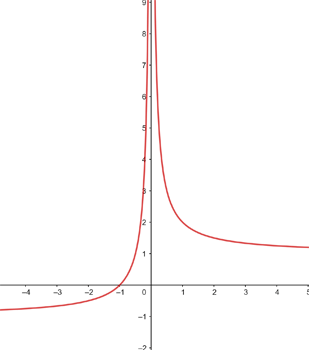
Estudo da continuidade da função:
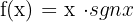
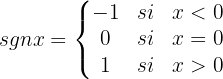
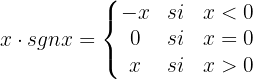
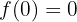
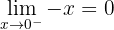
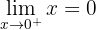
Trata-se de uma função contínua em toda ℛ.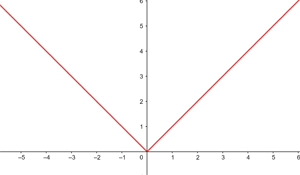
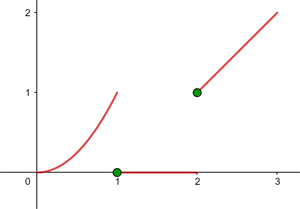
Estudo da continuidade da função no intervalo (0,3):
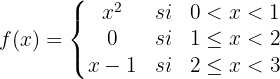
Só existe dúvidas sobre a continuidade da função nos pontos  e
e  , onde a forma da função muda.
, onde a forma da função muda.

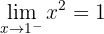

Salto = 
Em  existe uma descontinuidade de salto
existe uma descontinuidade de salto  .
.
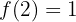
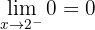
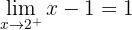
Salto = 
Em  existe uma descontinuidade de salto
existe uma descontinuidade de salto  .
.
Calcule os valores para garantir a função contínua
Calcule o valor de  para que a função a seguir seja contínua:
para que a função a seguir seja contínua:
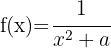
A função não é contínua quando: 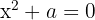
A equação tem solução apenas se  for negativo ou zero.
for negativo ou zero.
Portanto,  é contínua se
é contínua se  for positivo.
for positivo.
Calcule o valor de  para que a função a seguir seja contínua:
para que a função a seguir seja contínua:
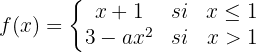
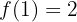
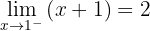
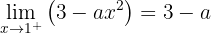
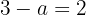
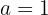
Calcule o valor de  para que a função a seguir seja contínua:
para que a função a seguir seja contínua:
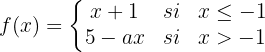
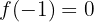
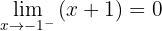
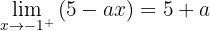
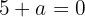
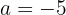
Calcule o valor de  para que a função a seguir seja contínua:
para que a função a seguir seja contínua:
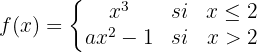
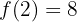
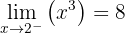
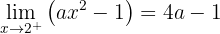
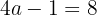
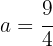
A seguinte função está definida por:
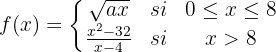
É contínua em 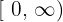 . Encontre o valor de
. Encontre o valor de  que faz com que essa afirmação seja verdadeira.
que faz com que essa afirmação seja verdadeira.
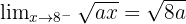
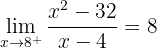
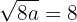

Resumir com IA:












