A análise de assíntotas é fundamental para entender o comportamento das funções nos extremos de seu domínio e em pontos críticos, onde a função pode tender ao infinito ou se tornar indeterminada. Por meio destes exercícios resolvidos, vamos explorar como encontrar assíntotas horizontais, verticais e oblíquas, utilizando técnicas algébricas e de cálculo.
Cada exercício será desenvolvido passo a passo, mostrando as estratégias para identificar as assíntotas de diferentes funções.
Encontre as assíntotas horizontais, verticais e oblíquas em cada um dos exercícios a seguir:

1 Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluimos que existe uma assíntota horizontal  .
.
2 Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota vertical 
3 Assíntota oblíqua
Calculamos, por meio de limites, a inclinação e a ordenada na origem das assíntotas oblíquas.


A assíntota oblíqua a assíntota horizontal.

1 Assíntota horizontal
Calculamos os limites quando tende a
tende a 

Concluimos que a assíntota horizontal é  .
.
2 Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A assíntota oblíqua é a mesma que a assíntota horizontal.

1 Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluimos que a assíntota horizontal é  .
.
2 Assíntota vertical
Calculamos os limites cuando  tiende a
tiende a 

A função tem uma assíntota vertical em 
3 Asíntota oblíqua
Calculamos, por meio de limites, a inclinação e a ordenada na origem das assíntotas oblíquas.


A assíntota oblíqua é a mesma que a assíntota horizontal 

1 Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluímos que a assíntota horizontal é  .
.
2 Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota vertical em 
3 Assíntota oblíqua
Calculamos, por meio de limites, a inclinação e a ordenada na origem das assíntotas oblíquas.


A assíntota oblíqua é a mesma que a assíntota horizontal 
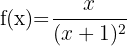
1 Assíntota horizontal
Calculamos os limites quando  tende a
tende a 
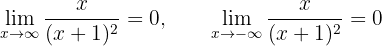
Concluímos que a assíntota horizontal é:  .
.
2 Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota vertical
3 Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas


A assíntota oblíqua é a mesma que a assíntota horizontal 

1 Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluímos que a assíntota horizontal é: .
.
2 Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota vertical

3 Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas.


A assíntota oblíqua é a mesma que a horizontal


1 Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluímos que a assíntota horizontal é:  .
.
2 Assíntota vertical
Calculamos os limites quando  tende a
tende a 


A função tem assíntotas verticais 
3 Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas


A assíntota oblíqua é a mesma que a horizontal 

1 Assíntota horizontal
Calculamos os limites quando  tiende a
tiende a 

Concluimos que não existem assíntotas horizontais.
2 Assíntota vertical
Calculamos os limites quando  tiende a
tiende a 

A função tem uma assíntota vertical

3 Assíntota obliqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas


A assíntota oblíqua é 

1 Assíntota horizontal
Calculamos os limites quando  tiende a
tiende a 

Concluímos que não existem assíntotas horizontais.
2 Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota vertical 
3 Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas
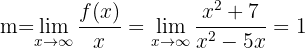

A assíntota oblíqua é 

1 Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluimos que no existen asíntotas horizontales.
2 Assíntota vertical
Calculamos os limites quando tiende a
tiende a 

A função tem uma assíntota vertical 
3 Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas
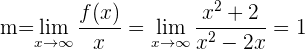

A assíntota oblíqua é: 

Assíntota horizontal
Calculamosos limites quando  tiende a
tiende a 

Concluímos que não existem assíntotas horizontais.
Assíntota vertical
Calculamos os límites quando  tiende a
tiende a 

A função tem uma assíntota vertical 
Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas


A assíntota oblíqua é: 

Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluímos que não existem assíntotas horizontais.
Assíntota vertical
Calculamos os limites quando tiende a
tiende a 

A função tem uma assíntota vertical 
Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas.

A função não possui assíntotas oblíquas.

Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluímos que não existem assíntotas horizontais.
Assíntota vertical
Calculamos os limites quando  tiende a
tiende a 

A função tem uma assíntota vertical 
Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas


A assíntota oblíqua é: 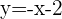

Assíntota horizontal
Calculamos os limites quando  tiende a
tiende a 

A função tem uma assíntota horizontal em 
A função não possui assíntotas verticais nem oblíquas.

Assíntota horizontal
Calculamos os limites quando  tiende a
tiende a 

A função tem uma assíntota horizontal em 
A função não possui assíntotas verticais nem oblíquas.

Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

Concluímos que não existem assíntotas horizontais.
Assíntota vertical
Calculamos os limites quando  tiende a
tiende a 

A função tem assíntota verticais 
Assíntota oblíqua
Calculamos, por meio de limites, o coeficiente angular e a ordenada na origem das assíntotas oblíquas


A assíntota oblíqua é 

Assíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

A assíntota horizontal é 
Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota vertical 
A função não possui assíntotas oblíquas.

Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

A função não possui assíntotas horizontal 
A função não possui assíntotas verticais nem oblíquas.

Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota horizontal 
A função não possui assíntotas verticais nem oblíquas.

Assíntota horizontal
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota horizontal 
Assíntota vertical
Calculamos os limites quando  tende a
tende a 

A função tem uma assíntota vertical 
A função não possui assíntotas oblíquas.
Resumir com IA:


