
Exercícios de probabilidade condicionada
Considerando  e
e  dois eventos aleatórios tendo
dois eventos aleatórios tendo  ,
,  ,
,  .
.
Determinar:
a. 
b. 
c. 
d. 
e. 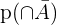
Considerando  e
e  dois eventos aleatórios tendo
dois eventos aleatórios tendo  ,
,  ,
,  .
.
Determinar:
a. 
São eventos dependentes

b. 
São eventos dependentes

c. 
Os eventos são compatíveis.

d. 
São eventos dependentes
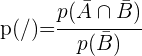
No numerador, aplicamos a lei de Morgan
No denominador, aplicamos a probabilidade do evento complementar

No numerador, aplicamos a probabilidade do evento complementar

e 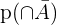
São eventos dependentes

No numerador aplicamos a lei de Morgan
No denominador, aplicamos a probabilidade do evento complementar

No numerador, aplicamos a probabilidade do evento complementar
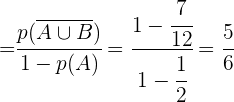
Considerando  e
e  dois eventos aleatórios tendo
dois eventos aleatórios tendo  ,
,  ,
,  .
.
Determinar:
a. 
b. 
c. 
d. 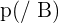
e. 
f. 
Considerando  e
e  dois eventos aleatórios tendo
dois eventos aleatórios tendo  ,
,  ,
,  .
.
Determinar:
a. 
São eventos dependentes

b. 
São eventos dependentes

c. 
São eventos compatíveis

d. 
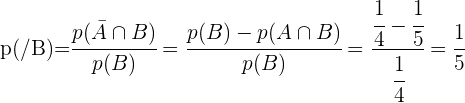
e 
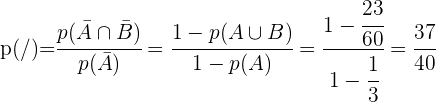
f. 
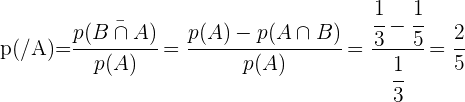
Problemas de probabilidade condicionada
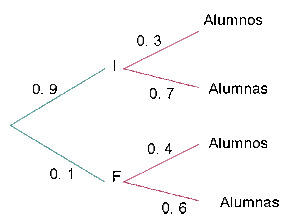
Em um centro escolar, os alunos podem optar por cursar como língua estrangeira inglês ou francês. Em um determinado curso,  dos alunos estuda inglês e os demais, francês.
dos alunos estuda inglês e os demais, francês. 
dos que estudam inglês são garotos e dos que estudam francês,  são garotos.
são garotos.
Escolhendo um aluno ao acaso, qual é a probabilidade de ser uma garota?
Em um centro escolar, os alunos podem optar por cursar como língua estrangeira inglês ou francês. Em um determinado curso,  dos alunos estuda inglês e o resto, francês.
dos alunos estuda inglês e o resto, francês.  dos que estudam inglês são garotos chicos e os garotos que estudam francês representam
dos que estudam inglês são garotos chicos e os garotos que estudam francês representam  . Escolhendo um aluno ao acaso, qual é a probabilidade de ser uma garota?
. Escolhendo um aluno ao acaso, qual é a probabilidade de ser uma garota?
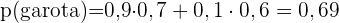
De um baralho com  cartas se tira simultaneamente duas cartas. Calcular a probabilidade de que:
cartas se tira simultaneamente duas cartas. Calcular a probabilidade de que:
a. As duas cartas sejam de copas
b. Pelo menos, uma carta seja de copas
c. Uma carta seja copa e a outra carta seja de espada
De um baralho com  cartas tiramos simultaneamente duas cartas.
cartas tiramos simultaneamente duas cartas.
Calcular a probabilidade de que:
a. As duas cartas sejam de copas
São eventos dependentes

b. Pelo menos, uma carta seja de copas

c. Uma carta de copas e uma carta de espada.
Pode tirar primeiro uma carta de copas e depois uma de espada. Ou primeiro uma carta de espada e depois uma carta de copas

Antes da prova, um aluno só havia estudado  dos
dos  temas correspondentes da matéria para a prova. A prova é feita escolhendo aleatoriamente dois tópicos e permitindo que o aluno escolha um dos dois temas para ser examinado.
temas correspondentes da matéria para a prova. A prova é feita escolhendo aleatoriamente dois tópicos e permitindo que o aluno escolha um dos dois temas para ser examinado.
Encontrar a probabilidade do aluno poder escolher um dos temas que ele estudou para a prova.
Antes de uma prova, um aluno só havia estudado  dos
dos  temas correspondentes à mesma matéria da prova. A prova é feita escolhendo aleatoriamente dois tópicos e permitindo que o aluno escolha um dos dois temas para ser examinado. Encontre a probabilidade do aluno poder escolher um dos temas que ele estudou para a prova.
temas correspondentes à mesma matéria da prova. A prova é feita escolhendo aleatoriamente dois tópicos e permitindo que o aluno escolha um dos dois temas para ser examinado. Encontre a probabilidade do aluno poder escolher um dos temas que ele estudou para a prova.
Uma sala de aula é formada por  meninos e
meninos e  meninas. Metade das meninas e metade dos meninos escolheram francês como disciplina opcional.
meninas. Metade das meninas e metade dos meninos escolheram francês como disciplina opcional.
a. Qual a probabilidade de que uma pessoa escolhida ao acaso seja um menino ou estude francês?
b. E a probabilidade de que seja uma menina e não estude francês?
Uma sala de aula é formada por  meninos e
meninos e  meninas; a metade das meninas e a metade dos meninos escolheram francês como disciplina opcional.
meninas; a metade das meninas e a metade dos meninos escolheram francês como disciplina opcional.
a. Qual a probabilidade de que uma pessoa escolhida ao acaso seja um menino ou estude francês?
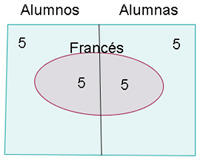
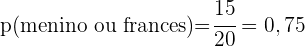
b. E a probabilidade de que seja uma menina e não estude francês?
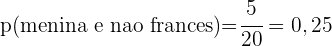
Uma oficina mecânica sabe que, em média, pela manhã chegam: três carros com problemas elétricos, oito com problemas mecânicos e três com problemas na lataria, e à tarde chegam dois com problemas elétricos, três com problemas mecânicos e um com problemas na lataria.
a. Fazer uma tabela organizando os dados informados pelo problema
b. Calcular a porcentagem dos que chegam à tarde para arrumar.
c. Calcular o percentual dos que chegam devido a problemas mecânicos
d. Calcular a probabilidade de que um carro com problemas elétricos apareça pela manhã.
Uma oficina mecânica sabe que, em média, pela manhã chegam: três carros com problemas elétricos, oito com problemas mecânicos e três com problemas na lataria, e à tarde chegam dois com problemas elétricos, três com problemas mecânicos e um com problemas na lataria.
a. Fazer uma tabela organizando os dados informados pelo problema
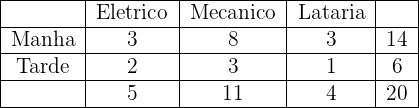
b. Calcular a porcentagem dos que chegam à tarde para arrumar

c. Calcular o percentual dos que chegam devido a problemas mecânicos

d. Calcular a probabilidade de que um carro com problemas elétricos apareça pela manhã.
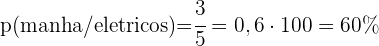
Uma sala é formada por  meninas e
meninas e  meninos. Se um comitê de três pessoas é escolhido aleatoriamente, a probabilidade de:
meninos. Se um comitê de três pessoas é escolhido aleatoriamente, a probabilidade de:
a. Selecionar três meninos
b. Selecionar exatamente dois meninos e uma menina
c. Selecionar, pelo menos, um menino
d. Selecionar exatamente duas meninas e um menino
Uma sala é formada por  meninas e
meninas e  meninos. Se um comitê de três pessoas é escolhido aleatoriamente, encontre a probabilidade de:
meninos. Se um comitê de três pessoas é escolhido aleatoriamente, encontre a probabilidade de:
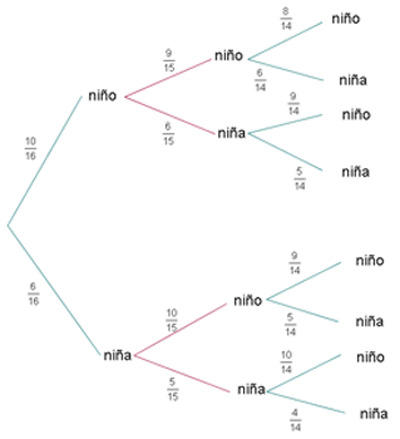
a. Selecionar três meninos
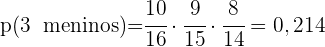
b. Selecionar exatamente dois meninos e uma menina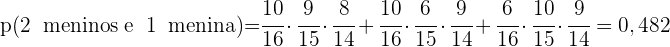
c. Selecionar pelo menos um menino
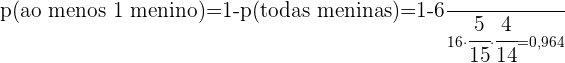
d. Selecionar exatamente duas meninas e um menino
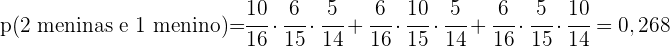
Uma caixa contém três moedas. Uma moeda é normal, outra tem duas caras e a terceira está viciada de modo que a probabilidade de obter cara é de  . Se uma moeda é selecionada para ser lançada ao ar, encontrar a probabilidade de que saia cara.
. Se uma moeda é selecionada para ser lançada ao ar, encontrar a probabilidade de que saia cara.
Uma caixa contém três moedas. Uma moeda é normal, outra tem dois lados iguais, e a terceira está viciada de tal forma que a probabilidade de obter cara é de  . Se uma moeda é selecionada para ser lançada ao ar, encontrar a probabilidade de que saia cara.
. Se uma moeda é selecionada para ser lançada ao ar, encontrar a probabilidade de que saia cara.
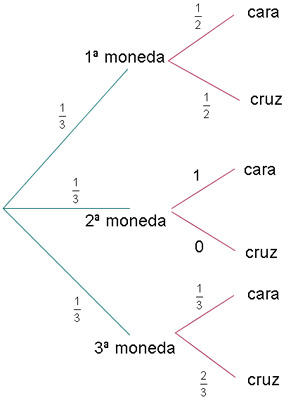

Uma urna contém  bolas vermelhas e
bolas vermelhas e  verdes. Uma bola é retirada e substituída por duas de outra cor. Em seguida, uma segunda bola é retirada. Pede-se:
verdes. Uma bola é retirada e substituída por duas de outra cor. Em seguida, uma segunda bola é retirada. Pede-se:
a. Probabilidade de que a segunda bola seja verde
b. Probabilidade de que as duas bolas retiradas sejam da mesma cor
Uma urna contém  bolas vermelhas e
bolas vermelhas e  verdes. Uma bola é retirada e substituída por duas de outra cor. Em seguida, uma segunda bola é retirada. Pede-se:
verdes. Uma bola é retirada e substituída por duas de outra cor. Em seguida, uma segunda bola é retirada. Pede-se:
a. Probabilidade de que a segunda bola seja verde
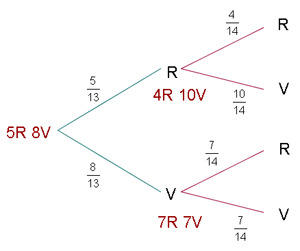

b. Probabilidade de que as duas bolas retiradas sejam da mesma cor

Em uma sala onde todos todos praticam algum esporte,  dos alunos joga futebol ou basquete e
dos alunos joga futebol ou basquete e  pratica ambos os esportes. Além disso, há
pratica ambos os esportes. Além disso, há  que não joga futebol, qual será a probabilidade de selecionar aleatoriamente um aluno da sala que:
que não joga futebol, qual será a probabilidade de selecionar aleatoriamente um aluno da sala que:
a. Jogue apenas futebol
b. Jogue apenas basquete
c. Pratique apenas um dos esportes.
d. Não jogue nem futebol nem basquete
Em uma sala onde todos todos praticam algum esporte,  dos alunos joga futebol ou basquete e
dos alunos joga futebol ou basquete e  pratica ambos os esportes. Além disso, há
pratica ambos os esportes. Além disso, há  que não joga futebol, qual será a probabilidade de selecionar aleatoriamente um aluno da sala que:
que não joga futebol, qual será a probabilidade de selecionar aleatoriamente um aluno da sala que:
a. Jogue apenas futebol
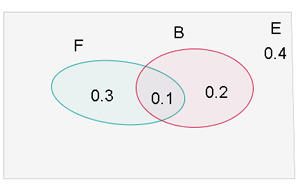
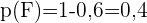

b. Jogue apenas basquete

c. Pratique apenas um dos esportes

d. Não jogue nem futebol, nem basquete

Em uma cidade,  de sua população tem cabelo castanho,
de sua população tem cabelo castanho,  tem olhos castanhos e
tem olhos castanhos e  tem cabelo e olhos castanhos. Se uma pessoa é escolhida aleatoriamente:
tem cabelo e olhos castanhos. Se uma pessoa é escolhida aleatoriamente:
a. Se tem cabelos castanhos, qual é a probabilidade de também ter olhos castanhos?
b. Se tem olhos castanhos, qual é a probabilidade de não ter cabelos castanhos?
c. Qual é a probabilidade de não ter cabelos nem olhos castanhos?
Em uma cidade,  de sua população tem cabelo castanho,
de sua população tem cabelo castanho,  tem olhos castanhos e
tem olhos castanhos e  tem cabelo e olhos castanhos. Se uma pessoa é escolhida aleatoriamente
tem cabelo e olhos castanhos. Se uma pessoa é escolhida aleatoriamente
a. Se tem cabelos castanhos, qual é a probabilidade de também ter olhos castanhos?
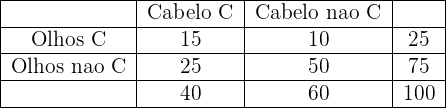
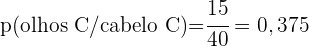
b. Se tem olhos castanhos, qual é a probabilidade de não ter cabelos castanhos?
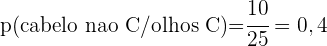
c. Qual é a probabilidade de não ter cabelos nem olhos castanhos?
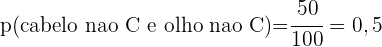
Em uma sala, tem  alunos, dos quais são:
alunos, dos quais são:  homens,
homens,  usam óculos e
usam óculos e  são homens e usam óculos. Se escolhemos aleatoriamente um aluno da sala:
são homens e usam óculos. Se escolhemos aleatoriamente um aluno da sala:
a. Qual é a probabilidade de ser mulher e não usar óculos?
b. Se sabemos que o aluno selecionado não usa óculos, qual é a probabilidade de ser homem?
Em uma sala, tem  alunos, dos quais são:
alunos, dos quais são:  homens,
homens,  usam óculos e
usam óculos e  são homens e usam óculos. Se escolhemos aleatoriamente um aluno da sala:
são homens e usam óculos. Se escolhemos aleatoriamente um aluno da sala:
a. Qual é a probabilidade de ser mulher e não usar óculos?
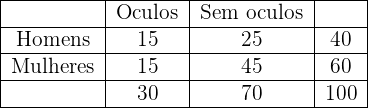

b. Se sabemos que o aluno selecionado não usa óculos, qual é a probabilidade de ser homem?

Temos duas urnas: a urna  contém
contém  bolas vermelhas e
bolas vermelhas e  bolas brancas, na urna
bolas brancas, na urna  contém
contém  bolas vermelhas e
bolas vermelhas e  bolas brancas. Ao lançar um dado, se aparecer um número menor que
bolas brancas. Ao lançar um dado, se aparecer um número menor que  ; nós vamos para a urna
; nós vamos para a urna  ; se o resultado é
; se o resultado é  ou mais, nós vamos para a urna
ou mais, nós vamos para a urna  . E em seguida, retiramos uma bola. Solicita-se:
. E em seguida, retiramos uma bola. Solicita-se:
a. Probabilidade de que a bola seja vermelha e da urna 
b. Probabilidade de que a bola seja branca
Temos duas urnas: a urna  contém
contém  bolas vermelhas e
bolas vermelhas e  bolas brancas, na urna
bolas brancas, na urna  contém
contém  bolas vermelhas e
bolas vermelhas e  bolas brancas. Ao lançar um dado, se aparecer um número menor que
bolas brancas. Ao lançar um dado, se aparecer um número menor que  ; nós vamos para a urna
; nós vamos para a urna  ; se o resultado é
; se o resultado é  ou mais, nós vamos para a urna
ou mais, nós vamos para a urna  .
.
E em seguida, retiramos uma bola. Solicita-se:
a. Probabilidade de que a bola seja vermelha e da urna 
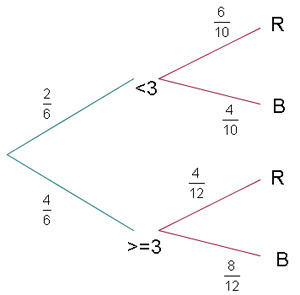

b. Probabilidade de que a bola seja branca
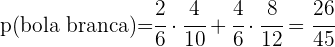
Um estudante conta com a ajuda de um despertador para uma prova, que consegue acordá-lo em  dos casos. Se ele ouve o despertador, a probabilidade de que faça a prova é de
dos casos. Se ele ouve o despertador, a probabilidade de que faça a prova é de  e, caso contrário, a probabilidade é de
e, caso contrário, a probabilidade é de  .
.
a. Se ele vai fazer a prova, qual é a probabilidade de que tenha ouvido o despertador?
b. Se ele não faz a prova, qual é a probabilidade de que não tenha ouvido o despertador?
Um estudante conta com a ajuda de um despertador para uma prova, que consegue acordá-lo em  dos casos. Se ele ouve o despertador, a probabilidade de que faça a prova é de
dos casos. Se ele ouve o despertador, a probabilidade de que faça a prova é de  e, caso contrário, a probabilidade é de
e, caso contrário, a probabilidade é de  .
.
a. Se ele vai fazer a prova, qual é a probabilidade de que tenha ouvido o despertador?
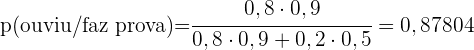
b. Se ele não faz a prova, qual é a probabilidade de que não tenha ouvido o despertador?
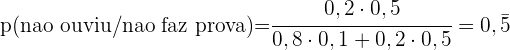
Em uma estante tem  romances e
romances e  livros de poesia. Uma pessoa
livros de poesia. Uma pessoa  escolhe um livro aleatoriamente na estante para levar. Em seguida, uma outra pessoa
escolhe um livro aleatoriamente na estante para levar. Em seguida, uma outra pessoa  escolhe outro livro aleatório.
escolhe outro livro aleatório.
a. Qual é a probabilidade do livro selecionado por B ser um romance?
b. Se sabe que B escolheu um romance, qual é a probabilidade do livro selecionado por A ser de poesia?
Em uma estante tem  romances e
romances e  livros de poesia. Uma pessoa
livros de poesia. Uma pessoa  escolhe um livro aleatoriamente na estante para levar. Em seguida, uma outra pessoa
escolhe um livro aleatoriamente na estante para levar. Em seguida, uma outra pessoa  escolhe outro livro aleatório.
escolhe outro livro aleatório.
a. Qual é a probabilidade do livro selecionado por  seja um romance?
seja um romance?
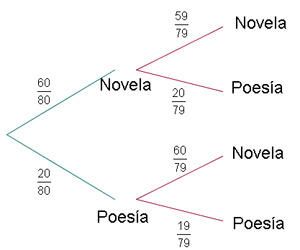
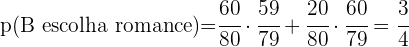
b. Se sabe que  escolheu um romance, qual a probabilidade que o livro selecionado por
escolheu um romance, qual a probabilidade que o livro selecionado por  seja um livro de poesia?
seja um livro de poesia?

Supõe-se que  de cada
de cada  homens e
homens e  de cada
de cada  mulheres usem óculos. Se o número de mulheres é quatro vezes superior ao de homens, pede-se a probabilidade de ser encontrado:
mulheres usem óculos. Se o número de mulheres é quatro vezes superior ao de homens, pede-se a probabilidade de ser encontrado:
a. Com uma uma pessoa sem óculos
b. Com uma mulher de óculos
Supõe-se que  de cada
de cada  homens e
homens e  de cada
de cada  mulheres usem óculos. Se o número de mulheres é quatro vezes superior ao de homens, pede-se a probabilidade de ser encontrado:
mulheres usem óculos. Se o número de mulheres é quatro vezes superior ao de homens, pede-se a probabilidade de ser encontrado:
a. Com uma uma pessoa sem óculos
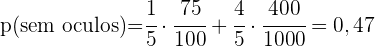
b. Com uma mulher de óculos
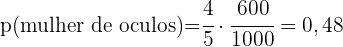
Em uma casa, há três chaveiros  e
e  ; o primeiro com cinco chaves, o segundo com sete e o terceiro com oito, Dentre as que apenas uma de cada chaveiro abre a porta do depósito. Um chaveiro é escolhido aleatoriamente e, dele, uma chave é selecionada para abrir o depósito. Solicita-se:
; o primeiro com cinco chaves, o segundo com sete e o terceiro com oito, Dentre as que apenas uma de cada chaveiro abre a porta do depósito. Um chaveiro é escolhido aleatoriamente e, dele, uma chave é selecionada para abrir o depósito. Solicita-se:
a. Qual será a probabilidade de acertar a chave?
b. Qual será a probabilidade do chaveiro escolhido ser o terceiro e a chave não abrir?
c. E se a chave escolhida for a correta, qual será a probabilidade de que ela pertença ao primeiro chaveiro  ?
?
Em uma casa, há três chaveiros  e
e  ; o primeiro com cinco chaves, o segundo com sete e o terceiro com oito, Dentre as que apenas uma de cada chaveiro abre a porta do depósito. Um chaveiro é escolhido aleatoriamente e, dele, uma chave é selecionada para abrir o depósito. Solicita-se:
; o primeiro com cinco chaves, o segundo com sete e o terceiro com oito, Dentre as que apenas uma de cada chaveiro abre a porta do depósito. Um chaveiro é escolhido aleatoriamente e, dele, uma chave é selecionada para abrir o depósito. Solicita-se:
a. Qual será a probabilidade de acertar a chave?

b. Qual será a probabilidade do chaveiro escolhido ser o terceiro e a chave não abrir?
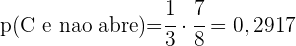
c. E se a chave escolhida for a correta, qual será a probabilidade de que ela pertença ao primeiro chaveiro A?
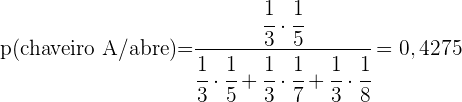
Resumir com IA:












