Uma matriz é uma estrutura matemática que permite organizar dados em linhas e colunas, facilitando a representação e o processamento de informações em diversos campos, como engenharia, física, economia e informática. Os exercícios com matrizes nos ajudam a entender como trabalhar com elas, desde operações básicas como soma e multiplicação até conceitos mais avançados, como a determinação das inversas.
Resolva os seguintes problemas:
Considere as matrizes:
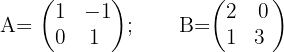
Calcule as somas e subtrações:
a)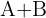 
b)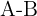 
a)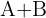
Somamos os elementos que estão na mesma posição em ambas as matrizes:
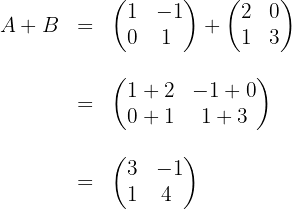
b)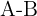
Subtraímos os elementos que estão na mesma posição em ambas as matrizes:
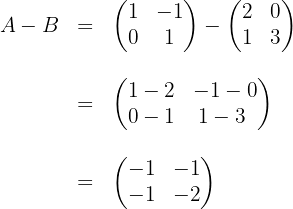
Dado as matrizes:
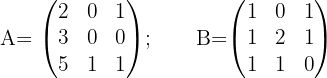
Calcule:
a)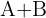
b)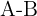
a)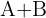
Somamos os elementos que estão na mesma posição em ambas as matrizes:
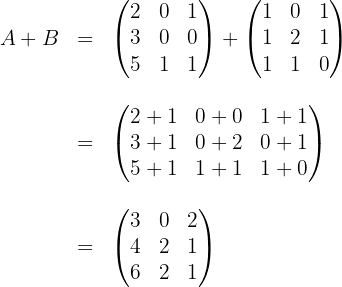
b)
Subtraímos os elementos que estão na mesma posição em ambas as matrizes:
Considerando as matrizes:
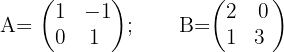
Verifique se a condição é atendida: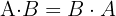 
a) Vamos calcular 
Multiplica-se a fila 
pela coluna 
(produto escalar) para obter o elemento 
.
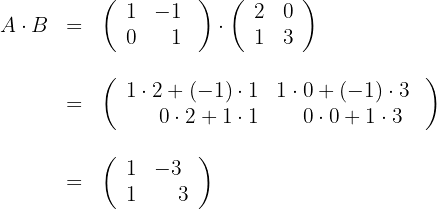
b) Calculamos 
Novamente, multiplica-se a fila pela coluna (produto escalar) para obter o elemento
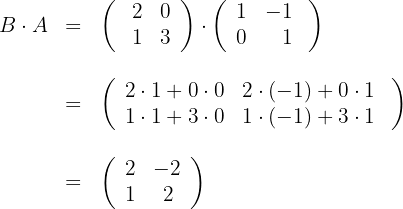
c) Podemos verificar que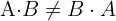 
Considerando as matrizes abaixo:
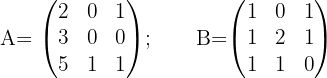
Verifique se satisfaz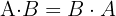
a) Calculamos
Vamos multiplicar a fila pela coluna 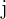(produto escalar) para obter o elemento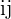
b) Calculamos
Multiplicando a fila pela coluna 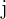(produto escalar) para obter o elemento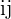
c) Pelo anterior, verificamos que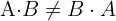
Considere as matrizes:
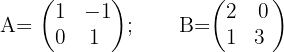
Calcule:
a) 
b) 
Lembramos que a transposta de uma matriz é obtida trocando as linhas pelas colunas.
a) Calculamos
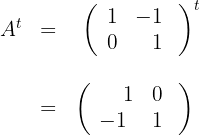
b) Calculamos
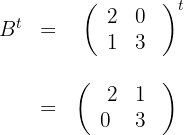
Dadas as matrizes
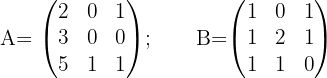
Calcule:
a)
b)
Lembramos que a transposta de uma matriz é obtida trocando as linhas pelas colunas.
a) Calculamos
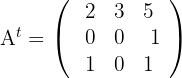
b) Calculamos
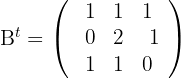
Considere as matrizes:
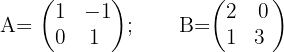
Calcule:
a)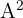 
b)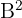 
a) Calculamos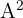
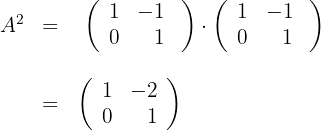
b) Calculamos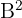
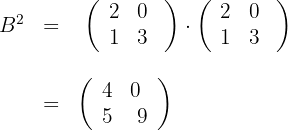
Dadas as matrizes
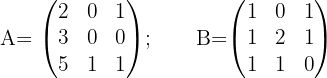
Calcule:
a)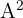
b)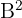
a) Calculamos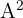
b) Calculamos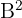
Encontre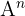 
para:
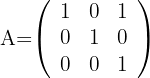
e 
a) Calculamos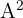
b) Calculamos 
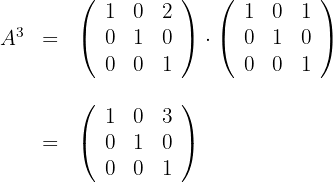
c) Podemos notar que o elemento que se encontra na posição 
coincide com a potência de 
, portanto, propomos para a potência 
d) Vamos checar se a fórmula proposta satisfaz a potência 
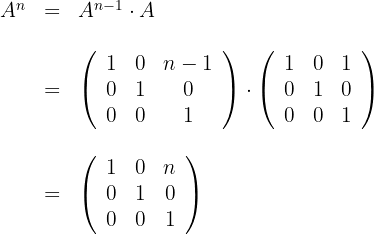
O cálculo anterior nos permite verificar que a fórmula proposta é válida para qualquer potência
Demonstre que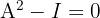 
, sendo:
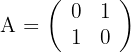
a) Calculamos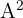
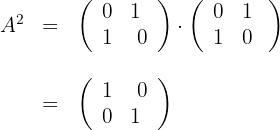
b) Substituímos do lado esquerdo da equação e calculamos:
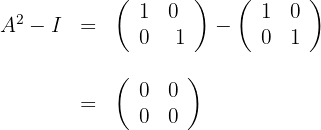
E assim, conseguimos demonstrar a igualdade solicitada.
a) Calculamos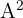
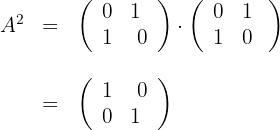
b) Substituímos do lado esquerdo da equação e calculamos:
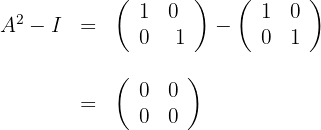
E assim, conseguimos demonstrar a igualdade solicitada.
Demonstre que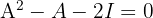 
, sendo:
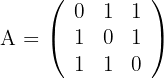
a) Calculamos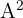
b) Substituímos do lado esquerdo da equação e calculamos
E assim, conseguimos demonstrar a igualdade solicitada.
Calcule a matriz inversa de:
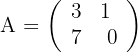
a) Construa uma matriz do tipo 
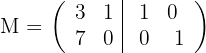
b) Utilize o método Gauss para transformar a metade da esquerda, , na matriz identidade, e a matriz que resulte do lado direito será a matriz inversa 
.
Dessa forma,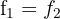 
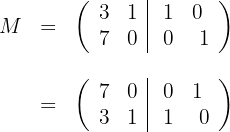
Calculamos,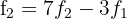 
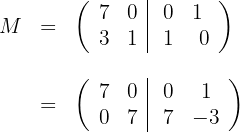
E então,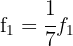 
e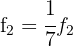 
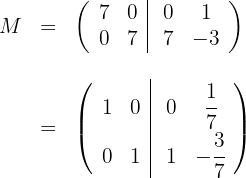
c) A matriz inversa é:
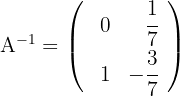
Calcule a matriz inversa de:
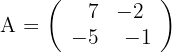
a) Construa um matriz do tipo
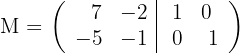
b) Utilize o método Gauss para transformar a metade do lado esquerdo, , na matriz identidade, e a matriz que obtenha do do lado direito, será a matriz inversa .
Sendo assim,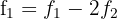 
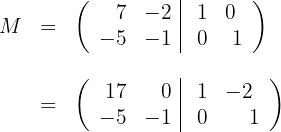
Calculamos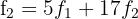 
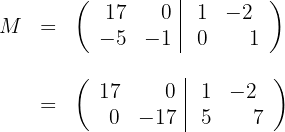
E então,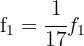 
y 
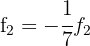
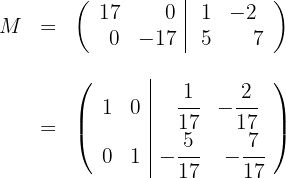
c) A matriz inversa é:
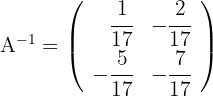
Calcule a matriz inversa de:
a) Construa uma matriz do tipo
b) Utilize o método Gauss para transformar o lado esquerdo, , na matriz identidade, e a matriz resultante do lado direito será a matriz inversa .
Portanto,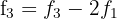 
Fazemos 
y 
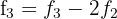
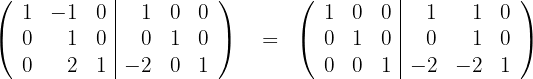
c) A matriz inversa é:
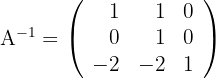
Descubra as matrizes e 
que correspondam ao sistema:
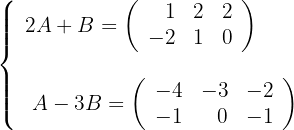
a) Vamos multiplicar a segunda equação por 
b) Somamos termo a termo e resolvemos para
c) Se multiplicarmos a primeira equação por 3 e somarmos termo a termo, obtemos:
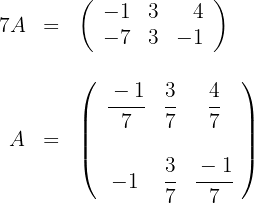
Uma fábrica produz dois modelos de lavadoras, e , em três versões: 
e 
.
Produção do modelo : 400 unidades na versão 
, 200 unidades na versão 
e 50 unidades na versão .
Produção do modelo : 300 unidades na versão , 100 unidades na versão e 30 unidades na versão .
A versão fica 25 horas na linha de produção e 1 hora na linha de administração. A versão fica 30 horas na linha de produção e 1.2 horas na linha de administração. A versão fica 33 horas na linha de produção e 1.3 horas na linha de administração.
a) Represente a informação em duas matrizes.
b) Encontre uma matriz que expresse as horas de oficina e de administração usadas para cada um dos modelos.
Matriz de produção:
Filas: Modelos 
; Colunas: Versões 
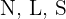
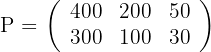
Matriz de custo em horas:
Filas: Versões 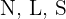; Colunas: Custo em horas: 
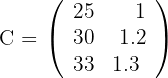
Matriz que expressa as horas de linha de produção e e administração para cada um dos modelos:
Calcule o seguinte posto matricial:
Realizamos operações elementares de linhas:
a) Assim: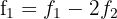 
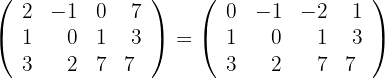
b) Em seguida: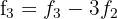 
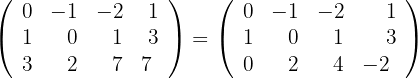
c) Calculamos, 
Sendo assim: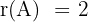 
.
Sendo:
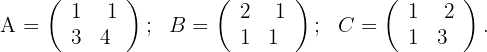
Calcule o valor de 
nas equações:
a)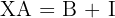 
b)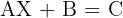 
c)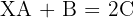 
d)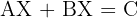 
e) 
Isolamos a variável de cada cada equação
a)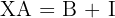
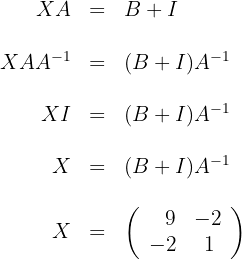
b)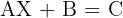
c)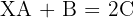
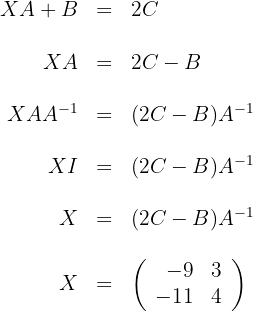
d)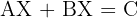
e)
Resolva o sistema na forma matricial:
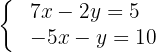
a) Vamos escrever na forma matricial
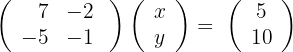
b) Resolvemos a equação
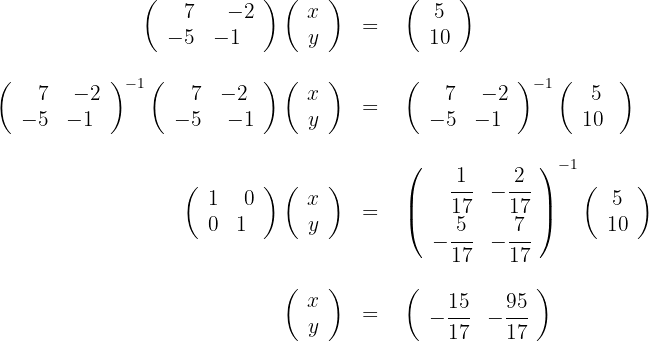
c) Portanto, a equação é:
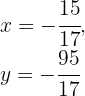
Resolva o sistema na forma matricial:
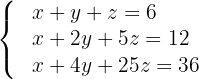
a) Vamos escrever na forma matricial
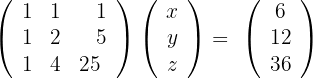
b) E resolver a equação
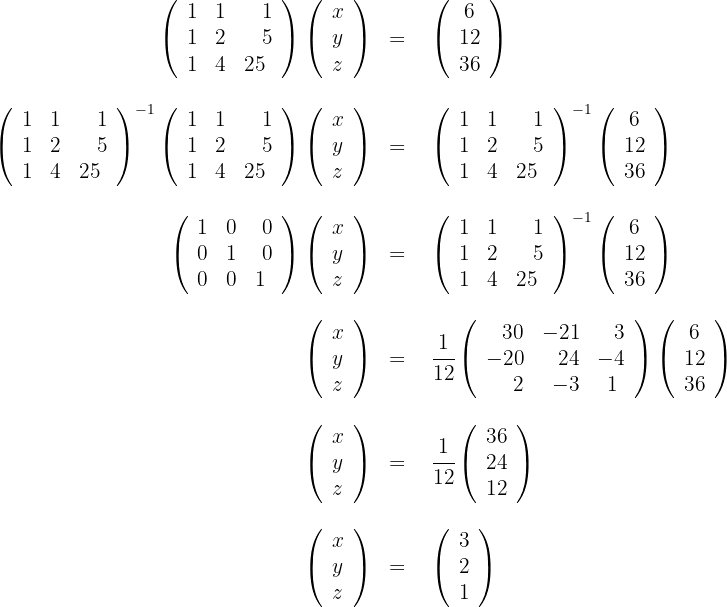
c) Dessa forma, a equação é a seguinte:
Gostou desse artigo? Deixe uma nota!
Loading...
