Temas
- Domínio em funções polinomiais
- Calcule o domínio das seguintes funções racionais
- Calcular o domínio das funções radicais
- Calcular o domínio das funções exponenciais
- Calcular o domínio das funções logarítmicas
- Calcular o domínio das funções trigonométricas
- Funções radicais e seu domínio
- Calcular o domínio da função
- Calcular o domínio da função definida por trechos
Lembrando que o domínio de uma função ou conjunto de saída se refere a: todos os valores que podem ser atribuídos à variável independente sem que a função se torne indefinida. Aqui, vamos estudar o domínio de funções reais, ou seja, funções cujo domínio e imagem são números reais ou subconjuntos deles.

Domínio em funções polinomiais
1. 
2. 
3. 
Calcular o domínio das funções polinomiais:
O domínio de uma função polinomial inteira é  , ou seja, todos os números reais.
, ou seja, todos os números reais.
1. 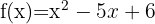

2. 

3. 
Observe que esta é uma função polinomial com coeficientes racionais.: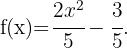 Portanto,
Portanto, 
Calcule o domínio das seguintes funções racionais
1 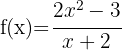
2 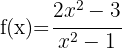
3 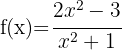
4 
5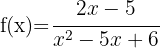
6 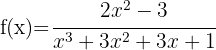
7 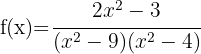
Calcule o domínio das funções racionais:
O domínio de uma função racional é  exceto os valores que anulam o denominador. Para encontrar o domínio, devemos igualar o denominador a zero e resolver a equação. As soluções dessa equação são os pontos que não pertencem ao domínio, já que anulam o denominador.
exceto os valores que anulam o denominador. Para encontrar o domínio, devemos igualar o denominador a zero e resolver a equação. As soluções dessa equação são os pontos que não pertencem ao domínio, já que anulam o denominador.
1. 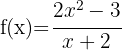

2. 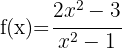

3. 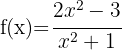
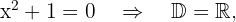
porque essa equação não tem raízes reais.
4.. 

porque a raiz é dupla.
5. 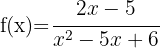
Tenemos que 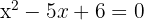 , então
, então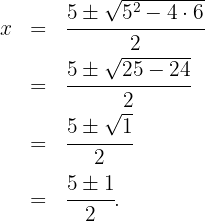
Assim,  ou
ou  . Portanto, o domínio é
. Portanto, o domínio é 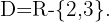
6. 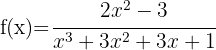
Observamos que o polinômio é o desenvolvimento de binômio ao cubo  porque
porque  é uma raiz tripla.
é uma raiz tripla.
7. 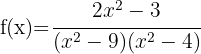
Fazendo o fator 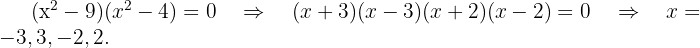
Portanto, 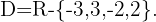
Calcular o domínio das funções radicais
1. 
2. 
3. 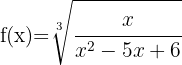
Calcule o domínio das funções radicais:
O domínio de uma função irracional de índice ímpar é 
1. 

2. 
O domínio dessa função são todos os números reais, exceto os valores nos quais o denominador da função racional dentro da raiz cúbica se anula. Assim,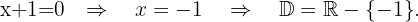
3. 
O domínio dessa função são todos os números reais, exceto os valores nos quais o denominador da função racional dentro da raiz cúbica se anula. Assim,
Calcular o domínio das funções exponenciais
1. 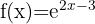
2. 
Calcule o domínio das funções exponenciais:
O domínio de uma função exponencial é 
1. 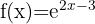

2. 
Como o expoente é racional,  não pertence ao domínio porque anula o denominador. Portanto,
não pertence ao domínio porque anula o denominador. Portanto,  .
.
Calcular o domínio das funções logarítmicas
1. 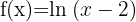
2. 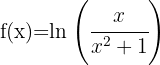
Calcule o domínio das funções logarítmicas:
Para que a função logaritmo esteja bem definida, seu argumento deve ser positivo. Ou seja, o domínio da função logarítmica é 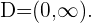
1. 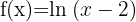
Resolvemos 
2. 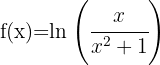
Como o denominador é sempre positivo, só vamos estudar o numerador. Desta forma:
 .
.
Calcular o domínio das funções trigonométricas
1. 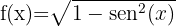
2. 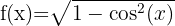
Calcule o domínio das funções trigonométricas:
O domínio de uma função irracional de índice par é formado pelo conjunto dos valores que fazem com que o radicando seja maior ou igual a zero. As funções trigonométricas seno e cosseno têm como domínio todos os números reais. Além disso, o valor máximo delas é 1, o que significa que essas funções sempre têm valores menores ou iguais a 1 para qualquer número real.
1. 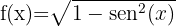
Vamos resolver 
2. 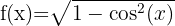
E resolvemos 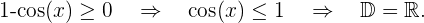
Funções radicais e seu domínio
Calcule o domínio das funções radicais:
O domínio de uma função irracional de índice par é formado pelo conjunto de valores para os quais o radical é maior ou igual a zero.
a) 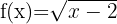
Resolvemos a desigualdade
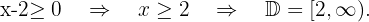
b) 
Resolvendo 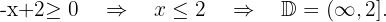
c) 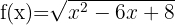
Resolvemos 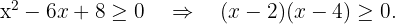 Igualamos a zero para obter as raízes
Igualamos a zero para obter as raízes 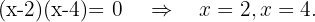
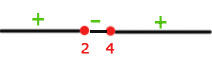
Por fim, vamos usar os intervalos nos quais a desigualdade é positiva. A união destes será nosso domínio. Portanto, 
d) 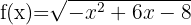
Resolvendo  igualamos a zero para obter as raízes
igualamos a zero para obter as raízes 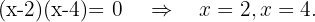

Finalmente, pegamos os intervalos nos quais a desigualdade é negativa. A união destes será nosso domínio. Portanto, 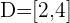
e) 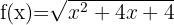
Resolvemos  porque
porque 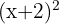 sempre é maior ou igual a zero.
sempre é maior ou igual a zero.
f) 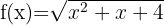
Resolvendo 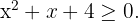 Se igualamos a zero, a equação correspondente não tem soluções reais. Além disso, notamos que, se tomamos qualquer valor será positivo ou zero. Portanto,
Se igualamos a zero, a equação correspondente não tem soluções reais. Além disso, notamos que, se tomamos qualquer valor será positivo ou zero. Portanto, 
g) 
Resolvemos  Observe que, essa desigualdade de restrição apenas se aplica ao valor
Observe que, essa desigualdade de restrição apenas se aplica ao valor  uma vez que para todos os demais valores de
uma vez que para todos os demais valores de  , o resultado é sempre negativo. Assim,
, o resultado é sempre negativo. Assim,  é o único valor que satisfaz nossa desigualdade e assim,
é o único valor que satisfaz nossa desigualdade e assim, 
h) 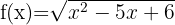
Resolvemos a desigualdade de segundo grau 
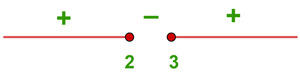
Finalmente, consideramos os intervalos nos quais a desigualdade é positiva, incluindo os extremos onde ela se anula. A união desses intervalos será nosso domínio. Portanto 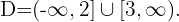
i) 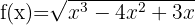
Resolvendo 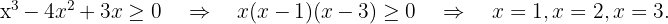
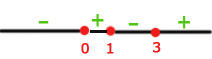
Por fim, tomamos os intervalos nos quais a desigualdade é positiva, incluindo os extremos onde ela se anula. A união desses intervalos será o nosso domínio. Portanto, 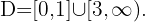
j) 
Como a raiz está no denominador, o radicando precisa ser maior que zero, mas não igual, pois nesse caso anularia o denominador. Resolvemos: 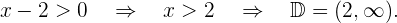
k) 
Neste caso, é necessário que o denominador seja diferente de zero e que a raiz do numerador seja maior ou igual a zero. Resolvendo: 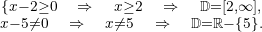 A solução é a interseção dos dois conjuntos, de forma que,
A solução é a interseção dos dois conjuntos, de forma que, 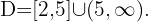
l) 
O numerador precisa ser maior ou igual a zero, e o denominador deve ser diferente de zero. Vamos resolver: 

A solução é a interseção dos dois conjuntos, portanto, 
m) 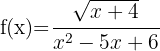
O denominador precisa ser maior que zero. Vamos resolver: 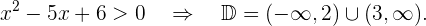

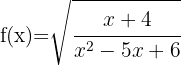
O radicando precisa ser maior que zero, e o denominador deve ser diferente de zero. Vamos resolver.  y
y 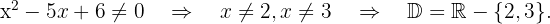

A solução é a interseção dos dois conjuntos, portanto, 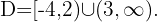
Encontre o domínio das seguintes funções polinomiais:
O domínio de uma função polinomial inteira é  , ou seja, todos os números reais.
, ou seja, todos os números reais.
a) 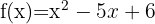

b) 

c) 
Observe que esta é uma função polinomial com coeficientes racionais: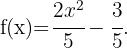 Portanto,
Portanto, 
d) 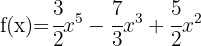
Observe que esta é uma função polinomial com coeficientes racionais, portanto, 
e) 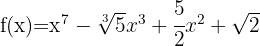
Observe que esta é uma função polinomial com coeficientes racionais e irracionais, portanto, 
Calcular o domínio da função
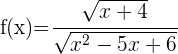
Calcule o domínio da função: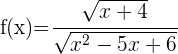
Resolvemos 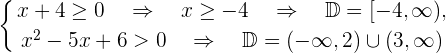 a solução é a interseção dos dois conjuntos, portanto,
a solução é a interseção dos dois conjuntos, portanto, 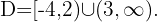

Calcule o domínio das seguintes funções racionais:
O domínio de uma função racional é  menos os valores que anulam o denominador. Para encontrar o domínio, devemos igualar o denominador a zero e resolver a equação. As soluções dessa equação são os pontos que não pertencem ao domínio, pois anulam o denominador.
menos os valores que anulam o denominador. Para encontrar o domínio, devemos igualar o denominador a zero e resolver a equação. As soluções dessa equação são os pontos que não pertencem ao domínio, pois anulam o denominador.
a) 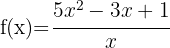
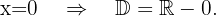
b) 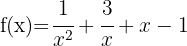
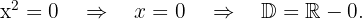
c) 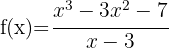
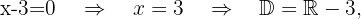
d) 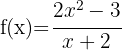
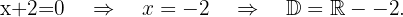
e) 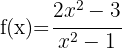
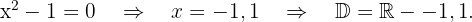
f) 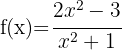
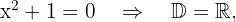
pois essa equação não tem raízes reais.
g) 
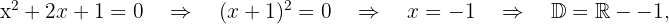
pois a raiz é dupla.
h) 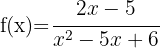
Temos que 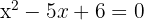 , então
, então
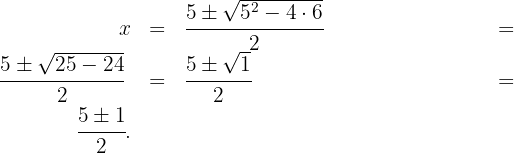
Assim,  ou
ou  . Portanto, o domínio é
. Portanto, o domínio é 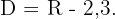
i) 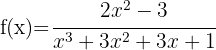
Observamos que o polinômio é o desenvolvimento de um binômio ao cubo 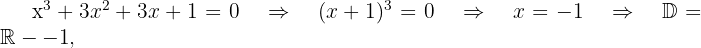
pois  é uma raiz tripla.
é uma raiz tripla.
j) 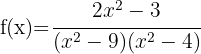
Fatorando 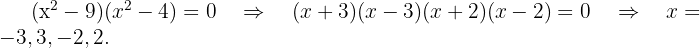
Portanto, 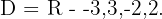
Calcular o domínio da função definida por trechos
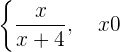
Calcule o domínio da função definida em trechos: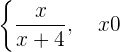
No primeiro trecho, é necessário que o denominador seja diferente de zero. No segundo trecho, sendo 3 uma constante que é sempre positiva, apenas estudamos se o denominador é maior que zero. Assim,
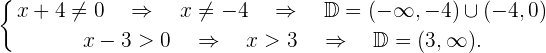
Finalmente, a solução é 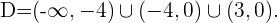
Encontre o domínio das seguintes funções radicais:
O domínio de uma função irracional de índice ímpar é 
O domínio de uma função irracional de índice par é obtido pelos pontos que satisfazem que o radicando seja maior ou igual a zero.
a) 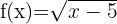
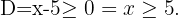
b) 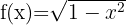
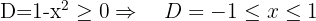
c) 

d) 
O domínio desta função são todos os reais, exceto os valores onde o denominador da função racional dentro da raiz cúbica se anula. Assim,
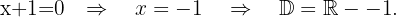
e) 
O domínio desta função são todos os reais, exceto os valores onde o denominador da função racional dentro da raiz cúbica se anula. Assim,
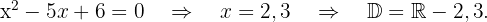
f) 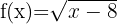
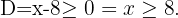
g) 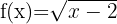
Resolvemos a desigualdade
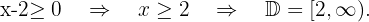
h) 
Resolvemos 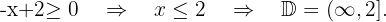
i) 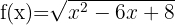
Resolvemos 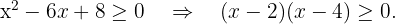 Igualamos a zero para obter as raízes latex(x-4)=0\quad\Rightarrow\quad x=2, x=4.[/latex]
Igualamos a zero para obter as raízes latex(x-4)=0\quad\Rightarrow\quad x=2, x=4.[/latex]
Finalmente, tomamos os intervalos em que a desigualdade é positiva. A união desses intervalos será o nosso domínio. Portanto, 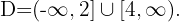
j) 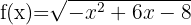
Resolvemos 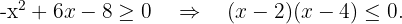 Igualamos a zero para obter as raízes latex(x-4)=0\quad\Rightarrow\quad x=2, x=4.[/latex]
Igualamos a zero para obter as raízes latex(x-4)=0\quad\Rightarrow\quad x=2, x=4.[/latex]
Finalmente, tomamos os intervalos em que a desigualdade é negativa. A união desses intervalos será o nosso domínio. Portanto, 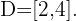
k) 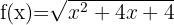
Resolvemos 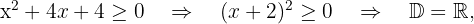 porque latex^2[/latex] é sempre maior ou igual a zero.
porque latex^2[/latex] é sempre maior ou igual a zero.
l) 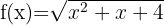
Resolvemos 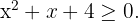 Se igualarmos a zero, a equação correspondente não tem soluções reais. Além disso, notamos que, se tomarmos qualquer valor, o resultado será positivo ou zero. Portanto,
Se igualarmos a zero, a equação correspondente não tem soluções reais. Além disso, notamos que, se tomarmos qualquer valor, o resultado será positivo ou zero. Portanto, 
m) 
Resolvemos 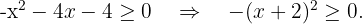 Observe que essa desigualdade só se cumpre para o valor
Observe que essa desigualdade só se cumpre para o valor  , já que para todos os outros valores de
, já que para todos os outros valores de  , o resultado é sempre negativo. Assim,
, o resultado é sempre negativo. Assim,  é o único valor que satisfaz nossa desigualdade e, portanto,
é o único valor que satisfaz nossa desigualdade e, portanto, 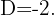
n) 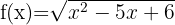
Resolvemos a desigualdade de segundo grau 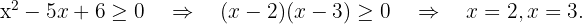
Finalmente, tomamos os intervalos em que a desigualdade é positiva, com os extremos onde se anula incluídos. A união desses intervalos será o nosso domínio. Portanto, 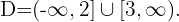
o) 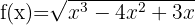
Resolvemos 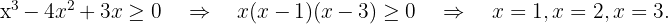
Finalmente, tomamos os intervalos em que a desigualdade é positiva, com os extremos onde se anula incluídos. A união desses intervalos será o nosso domínio. Portanto, 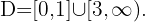
p) 
Como a raiz está no denominador, o radicando deve ser maior que zero, mas não igual, pois isso anularia o denominador. Resolvemos 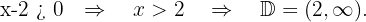
q) 
Neste caso, devemos garantir que o denominador seja diferente de zero e a raiz do numerador seja maior ou igual a zero. Resolvemos 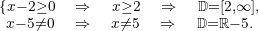 A solução é a interseção dos dois conjuntos, portanto,
A solução é a interseção dos dois conjuntos, portanto, 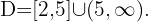
r) 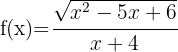
O numerador deve ser maior ou igual a zero e o denominador diferente de zero. Resolvemos 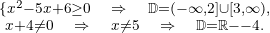
A solução é a interseção dos dois conjuntos, portanto, 
s) 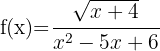
O denominador deve ser maior que zero. Resolvemos 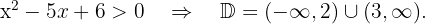
t) 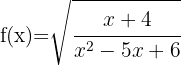
O radicando deve ser maior que zero e o denominador diferente de zero. Resolvemos 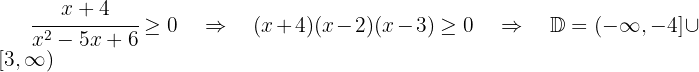 e
e 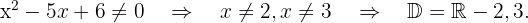
A solução é a interseção dos dois conjuntos, portanto, 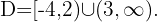
Resumir com IA: